A company manufacture is bicyles and tricycles each of which must be processed through machines A and B. Machine A has maximum of 120 hours avaiable and machine B has maximum of 180 hours available hours on machine A and 3 hours on machine B. Machine A and 10 hours on machine B.
If profit are ₹ 180 for a bicyle and ₹ 220 for a tricyle , formulate and solve the L.P.P to determine the number of bicycles and tricycle that should be manufactured in order to maximize the profit .
Let x no. of bicycles and y no.of tricycle are to be manufactured . Then, total profit Z = (180 x + 220 y) which is to be maximized.

From table, we have
6x+4y≤120,3x+10y≤180
x≥0,y≥0
(∵ no . of bicycles and tricyles cannot be negative)
The mathematical formulation of given LPP is
Maximie Z = 180 x + 220y
such that 6x+4y≤120,
3x+10y≤180
x≥0,y≥0
Now , darw the line AB and CD of equations 6x4y=120 and 3x+10y=180 respectively
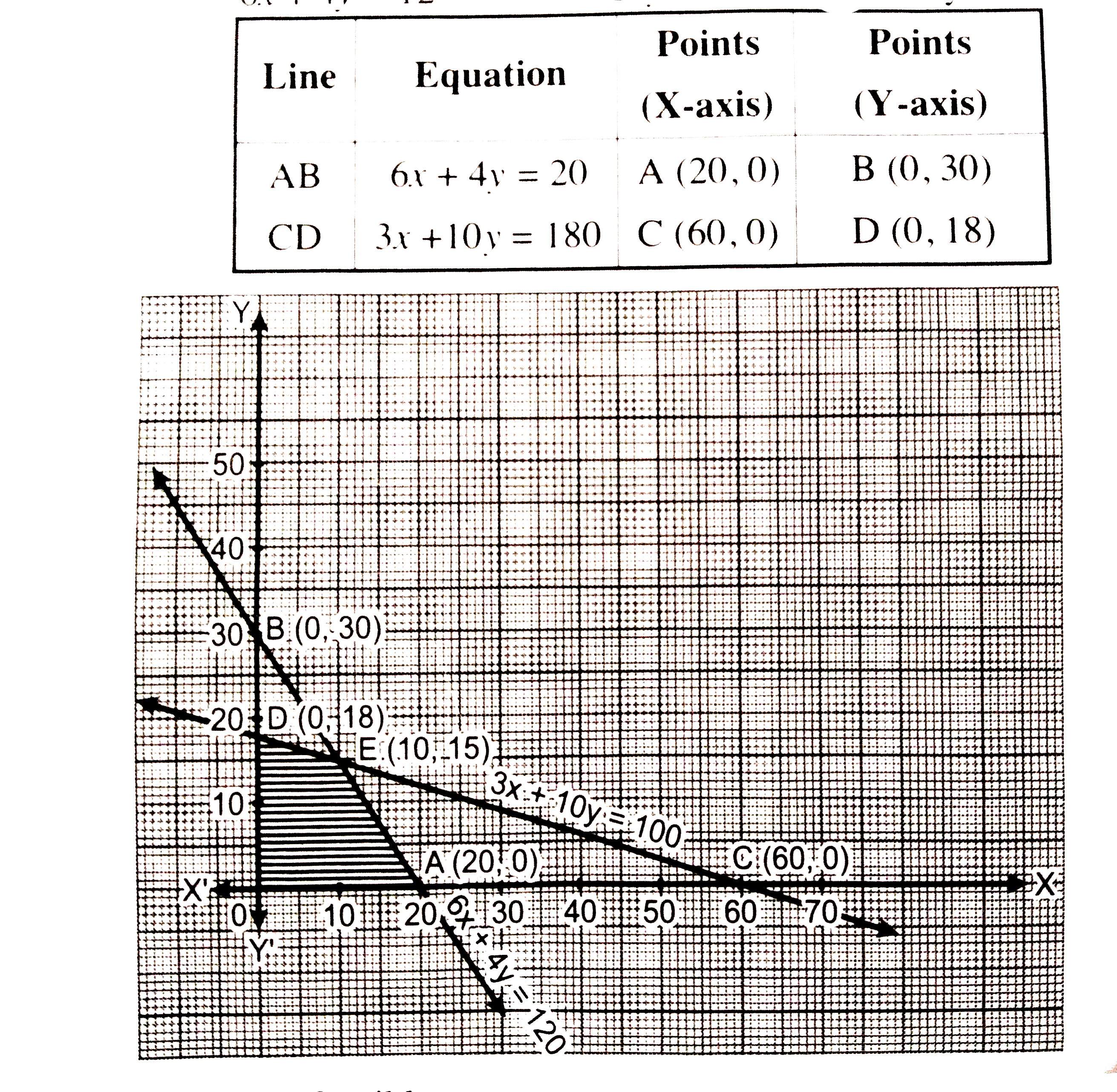
The feasible region is OAEDO with O(0,0),A(20,0)EandD(0,18)
E is the point of intersection of the lines.
3x+10y=180, .......(1)
and 6x+4y=120 .....(2)
Multiplying equation (1) by 2 and subtracting equation (2) form it , we get
6x+20y=3606x+4y=120− − −¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ 16y=240
⇒y=15
Putting y= 15 in equation (1), we get x = 10
∴E(10,15)
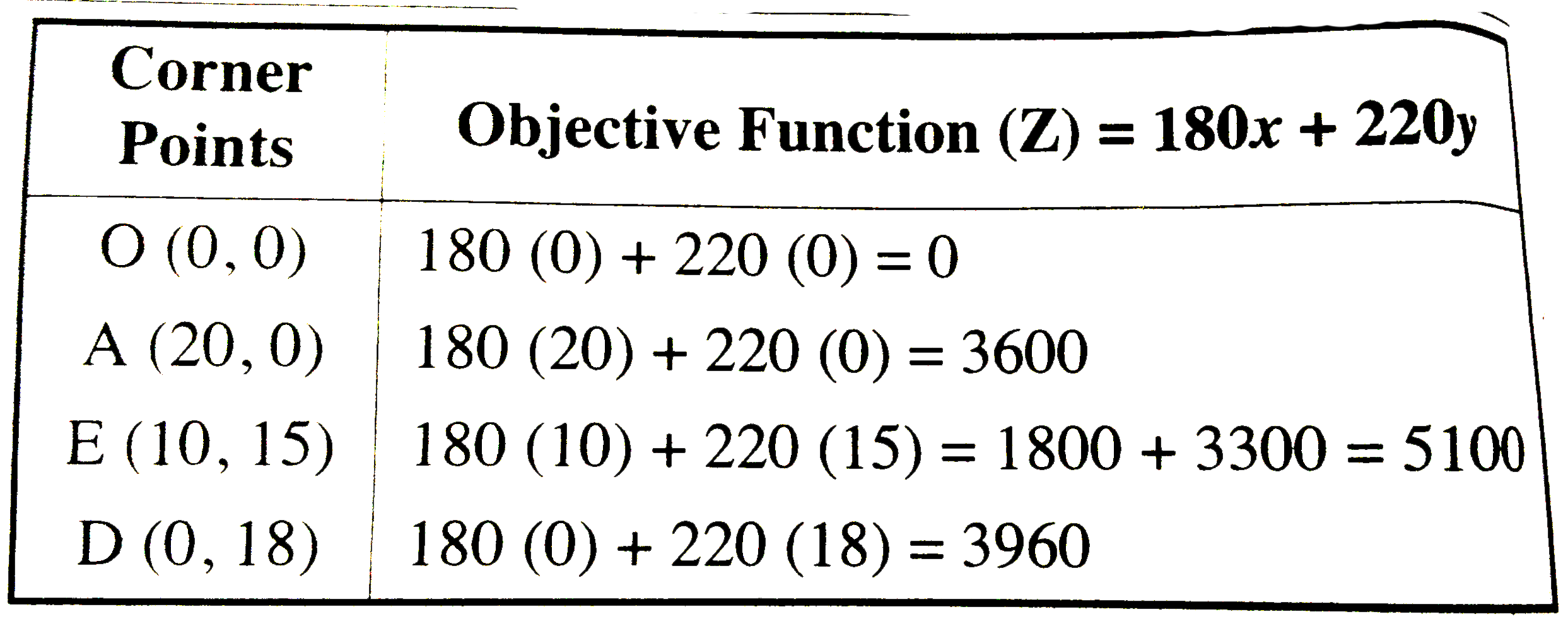
Hence, the maximum value of Z is 5100 at E (10, 15) i.e., 10 bicyles and15 tricyles should be manufactured to maximize the profit.
Topper's Solved these Questions
- JULY 2017BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - JULY 2017EXERCISE - SECTION - II
20 Videos
- JULY 2016BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - JULY 2016EXERCISE - Section-II
20 Videos
- JULY 2018BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - JULY 2018EXERCISE - SECTION II
20 Videos
Similar Questions
A company manufactures bicycles and tricycles, each of which must be processed through two machines A and B. Machine A has maximum of 120 hours available and machine B has a maximum of 180 hours available. Manufacturing a bicycle requires 6 hours on machine A and 3 hours on machine B. Manufacturing a tricycle requires 4 hours on machine A and 10 hours on machine B.
If profits are ₹ 180 for a bicycle and ₹ 220 for a tricycle, determine the number of bicycles and tricycles that should be manufactured in order to maximize the profit.
View SolutionA toy manufacturing farm produces toys T1andT2 each of which must be processed through two machines M1andM2. The maximum availablity of machines M1andM2 per day are 14 hours and 20 hours respectively. Manufacturing of toy T1, requires 5 hours on machine M1 If the 3 hours on machine M2 whereas toy T2, requires 4 hours on machine M1, and 6 hours on machine M2. If the profit on manufacturing of toy T, is Rs.50 and profit on manufacturing of toy T2 is Rs.70, formulate this problem as L.P.P. in order to maximize the profit.
View Solution
Knowledge Check
A printing company prints two types of magzines A and B. The company earns Rs. 20 and Rs. 30 on each copy of magazines A and B respectively. The magazine A requires 2 hours on machine I, 4 hours on Machine II and 2 hours machine III. Magazine B requires 3 hours on machine I, 5 hours on machine II and 3 hours on machine III. Machines I,II, III are available for 35, 50 and 70 hours per week respectively. Formulate the LPP to determine weekly production of magazines A and B, so that the total profit is maximum
AMaximize z=20x+3y subject to 2x+3y≤35,4x+5y≤50,2x+3y≥70,x≥0,y≥0BMaximize z=20x+3y subject to 2x+3y≤35,4x+5y≤50,2x+3y≤70,x≥0,y≥0CMaximize z=20x+3y subject to 2x+3y≤35,4x+5y≥50,2x+3y≤70,x≥0,y≥0DMaximize z=20x+3y subject to 2x+3y≥35,4x+5y≤50,2x+3y≤70,x≥0,y≥0
In a small scale industry, a manufacturer produces two types of book cases. The first type of book case requires 3 hours on machine A and 2 hours on machine B for completion whereas the second type of book case requires 3 hours on machine A and 3 hours on machine B. The machines A and B respectively run for at the most 18 hours and 14 hours per day. He earns a profit of 30 on each type of case of first type and 40 on each book case of second type. How many book cases of each type should he manufacture so as to have maximum profit. Make it an LPP and solve it graphically.
View SolutionA furniture form manufactures chairs and tables, each requiring the use of three machines A, B and C. Production of one chair requires 2 hours on machine A, 1 hour on machine B, and 1 hour on machine C. Each table requires 1 hour each on machines A and B and 3 hours on machine C. Profit realized by selling one chair is Rs. 30 while for a table the figure is Rs. 60. The total time available per week on machine A is 70 hours, on machine B is 40 hours, and on machine C is 90 hours. How many chairs and table should be made per week so as to maximize profit? Develop a mathematical formulation.
View SolutionA furniture form manufactures chairs and tables, each requiring the use of three machines A, B and C. Production of one chair requires 2 hours on machine A, 1 hour on machine B, and 1 hour on machine C. Each table requires 1 hour each on machines A and B and 3 hours on machine C. Profit realized by selling one chair is Rs. 30 while for a table the figure is Rs. 60. The total time available per week on machine A is 70 hours, on machine B is 40 hours, and on machine C is 90 hours. How many chairs and table should be made per week so as to maximize profit? Develop a mathematical formulation.
View SolutionA manufacturer produces two types of steel trunks. He has tow machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs. 30 and Rs. 25 per trunk of the first type and the second respectively. How many trunks of each type must he make each day to makes maximum profit?
View SolutionA manufacture produceds two types of steel trunks. He has two machines, A and B. The first type of book case requires 3 hours on machine A and 3 hours on machine B for completion whereas the second type required 3 hours on machine A and 2 hours n machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs.30 and Rs.25 per trunk of the first type and second type respectively. How many trunks of each type must he make each day to make the maximum profit?
View SolutionManufacturer produces two types of steel trunks. He has two machines, A and B. The first type of trunk requires 3 hours on machine A and 3 hours on machine B. The second type requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs. 30 per trunk on the first type of trunk and Rs. 25 per trunk on the second type. Formulate a linear programming problem to find out how many trunks of each type he must make each day to maximize his profit.
View SolutionA factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftmans time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftmans time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsmans time. If the profit on a racket and on a bat is Rs. 20 and Rs. 10 respectively, find the number of tennis rackets and crickets bats that the factory must manufacture to earn the maximum profit. Make it as an L.P.P. and solve graphically.
View Solution
