A manufacturer produces two types of steel trunks. He has tow machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs. 30 and Rs. 25 per trunk of the first type and the second respectively. How many trunks of each type must he make each day to makes maximum profit?
To solve the problem of maximizing the profit from producing two types of steel trunks using linear programming, we will follow these steps:
Step 1: Define the Variables
Let:
- X = number of trunks of the first type produced
- Y = number of trunks of the second type produced
Step 2: Formulate the Constraints
From the problem statement, we have the following constraints based on the machine hours:
1. For Machine A:
- The first type of trunk requires 3 hours and the second type requires 3 hours.
- Total hours used on Machine A cannot exceed 18 hours:
3X+3Y≤18
Simplifying this gives:
X+Y≤6(Constraint 1)
2. For Machine B:
- The first type of trunk requires 3 hours and the second type requires 2 hours.
- Total hours used on Machine B cannot exceed 15 hours:
3X+2Y≤15(Constraint 2)
3. Non-negativity constraints:
X≥0,Y≥0
Step 3: Formulate the Objective Function
The profit from each type of trunk is given as:
- Profit from the first type = Rs. 30 per trunk
- Profit from the second type = Rs. 25 per trunk
Thus, the objective function to maximize profit Z is:
Z=30X+25Y
Step 4: Graph the Constraints
To find the feasible region, we will graph the constraints:
1. Graph of Constraint 1: X+Y=6
- Intercepts: (6,0) and (0,6)
2. Graph of Constraint 2: 3X+2Y=15
- Intercepts:
- For X: Set Y=0 → 3X=15 → X=5 → Point (5,0)
- For Y: Set X=0 → 2Y=15 → Y=7.5 → Point (0,7.5)
Step 5: Identify the Feasible Region
The feasible region is where the constraints overlap. It is bounded by the lines X+Y=6 and 3X+2Y=15 along with the axes.
Step 6: Find the Corner Points
The corner points of the feasible region are:
1. (0,0)
2. (5,0)
3. (0,6)
4. Intersection of X+Y=6 and 3X+2Y=15
To find the intersection point:
- From X+Y=6, we can express Y=6−X.
- Substitute into 3X+2(6−X)=15:
3X+12−2X=15⟹X=3
- Substitute X=3 back into Y=6−X:
Y=6−3=3
Thus, the intersection point is (3,3).
Step 7: Evaluate the Objective Function at Each Corner Point
1. At (0,0):
Z=30(0)+25(0)=0
2. At (5,0):
Z=30(5)+25(0)=150
3. At (0,6):
Z=30(0)+25(6)=150
4. At (3,3):
Z=30(3)+25(3)=90+75=165
Step 8: Determine the Maximum Profit
The maximum profit occurs at the point (3,3), which means:
- The manufacturer should produce 3 trunks of the first type and 3 trunks of the second type.
Conclusion
To maximize profit, the manufacturer should produce:
- 3 trunks of the first type
- 3 trunks of the second type
Let:
- X = number of trunks of the first type produced
- Y = number of trunks of the second type produced
From the problem statement, we have the following constraints based on the machine hours:
- The first type of trunk requires 3 hours and the second type requires 3 hours.
- Total hours used on Machine A cannot exceed 18 hours:
3X+3Y≤18
Simplifying this gives:
X+Y≤6(Constraint 1)
- The first type of trunk requires 3 hours and the second type requires 2 hours.
- Total hours used on Machine B cannot exceed 15 hours:
3X+2Y≤15(Constraint 2)
X≥0,Y≥0
The profit from each type of trunk is given as:
- Profit from the first type = Rs. 30 per trunk
- Profit from the second type = Rs. 25 per trunk
Z=30X+25Y
To find the feasible region, we will graph the constraints:
- Intercepts: (6,0) and (0,6)
- Intercepts:
- For X: Set Y=0 → 3X=15 → X=5 → Point (5,0)
- For Y: Set X=0 → 2Y=15 → Y=7.5 → Point (0,7.5)
The feasible region is where the constraints overlap. It is bounded by the lines X+Y=6 and 3X+2Y=15 along with the axes.
The corner points of the feasible region are:
1. (0,0)
2. (5,0)
3. (0,6)
4. Intersection of X+Y=6 and 3X+2Y=15
- From X+Y=6, we can express Y=6−X.
- Substitute into 3X+2(6−X)=15:
3X+12−2X=15⟹X=3
- Substitute X=3 back into Y=6−X:
Y=6−3=3
Thus, the intersection point is (3,3).
1. At (0,0):
Z=30(0)+25(0)=0
2. At (5,0):
Z=30(5)+25(0)=150
3. At (0,6):
Z=30(0)+25(6)=150
4. At (3,3):
Z=30(3)+25(3)=90+75=165
The maximum profit occurs at the point (3,3), which means:
- The manufacturer should produce 3 trunks of the first type and 3 trunks of the second type.
To maximize profit, the manufacturer should produce:
- 3 trunks of the first type
- 3 trunks of the second type
Topper's Solved these Questions
Similar Questions
Manufacturer produces two types of steel trunks. He has two machines, A and B. The first type of trunk requires 3 hours on machine A and 3 hours on machine B. The second type requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs. 30 per trunk on the first type of trunk and Rs. 25 per trunk on the second type. Formulate a linear programming problem to find out how many trunks of each type he must make each day to maximize his profit.
View SolutionState the types of motion of the needle of a sewing machine
View SolutionA manufacturing companu makes two types of teaching aids A and B of Mathematics for Class X. Each type of A requires 9 labour hours for fabircating and 1 labour for finishing. Each type of B requires 12 labour hours for fabircating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available per week are 180 and 30 respectively. The company makes a profit of 80 on each piece of type A and 120 on each piece of type B. How many pieces of type A and types B should be manufactured per week to get a maximum profit? Formulae this as Linear Programming Problems and solved it. Identify the feasible region from the rough sketch.
View SolutionA furniture form manufactures chairs and tables, each requiring the use of three machines A, B and C. Production of one chair requires 2 hours on machine A, 1 hour on machine B, and 1 hour on machine C. Each table requires 1 hour each on machines A and B and 3 hours on machine C. Profit realized by selling one chair is Rs. 30 while for a table the figure is Rs. 60. The total time available per week on machine A is 70 hours, on machine B is 40 hours, and on machine C is 90 hours. How many chairs and table should be made per week so as to maximize profit? Develop a mathematical formulation.
View SolutionA manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs 17.50 per package on nuts and Rs 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machine for at most 12 hours a day?
View SolutionA machine does 392 J of work in 4 seconds. What is the power of the machine?
View SolutionSimple machines
View Solution(Manufacturing problem) A manufacturing company makes two models A and B of a product. Each piece of Model A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each piece of Model B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available are 180 and 30 respectively. The company makes a profit of Rs 8000 on each piece of model A and Rs 12000 on each piece of Model B. How many-pieces of Model A and Model B should be manufactured per week to realise a maximum profit? What is the maximum profit per week?
View SolutionA manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at Rs. 7 profit and that of B at a profit of Rs. 4. Find the production level per day for maximum profit graphically.
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the tune (in minutes) required for each toy on the machines is given below:
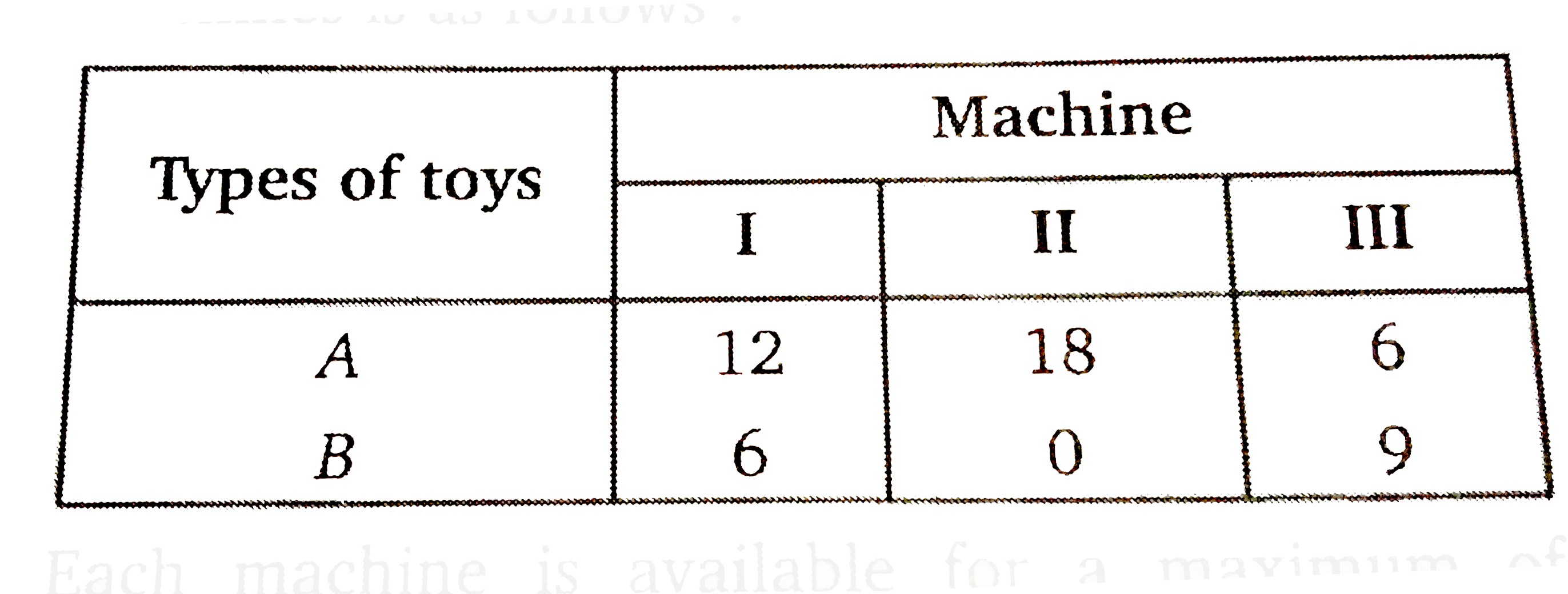 Each machine is available for a
maximum of 6 hours per day. If the profit
Each machine is available for a
maximum of 6 hours per day. If the profit
View Solution
