A cylinder has a base radius of 2 and a height of 9 . To the nearest whole number , by how much does the lateral area exceed the sum of the areas of the two bases ?
101
96
88
81
The correct Answer is:C
To solve the problem step by step, we will calculate the lateral area of the cylinder and the sum of the areas of the two bases, and then find the difference between them.
Step 1: Calculate the Lateral Area of the Cylinder
The formula for the lateral area AL of a cylinder is given by:
AL=2πrh
where r is the radius and h is the height.
Given:
- Radius r=2
- Height h=9
Substituting the values into the formula:
AL=2π(2)(9)=36π
Step 2: Calculate the Area of One Base
The area AB of one base of the cylinder (which is a circle) is given by:
AB=πr2
Substituting the radius:
AB=π(22)=4π
Step 3: Calculate the Sum of the Areas of Two Bases
Since there are two bases, the total area Atotal_bases of the two bases is:
Atotal_bases=2×AB=2×4π=8π
Step 4: Calculate the Difference Between the Lateral Area and the Sum of the Areas of the Bases
Now, we need to find out by how much the lateral area exceeds the sum of the areas of the two bases:
Difference=AL−Atotal_bases
Substituting the values:
Difference=36π−8π=28π
Step 5: Convert the Difference to a Numerical Value
To find the numerical value, we can approximate π as 3.14:
28π≈28×3.14≈87.92
Rounding this to the nearest whole number gives:
Difference≈88
Final Answer
The lateral area exceeds the sum of the areas of the two bases by approximately 88.
---
The formula for the lateral area AL of a cylinder is given by:
AL=2πrh
where r is the radius and h is the height.
- Radius r=2
- Height h=9
AL=2π(2)(9)=36π
The area AB of one base of the cylinder (which is a circle) is given by:
AB=πr2
AB=π(22)=4π
Since there are two bases, the total area Atotal_bases of the two bases is:
Atotal_bases=2×AB=2×4π=8π
Now, we need to find out by how much the lateral area exceeds the sum of the areas of the two bases:
Difference=AL−Atotal_bases
Substituting the values:
Difference=36π−8π=28π
To find the numerical value, we can approximate π as 3.14:
28π≈28×3.14≈87.92
Rounding this to the nearest whole number gives:
Difference≈88
The lateral area exceeds the sum of the areas of the two bases by approximately 88.
Topper's Solved these Questions
Similar Questions
A cylinder has a surface area of 360π and height of 3. What is the diameter of the cylinder's circular base?
View SolutionA right circular cone and a right circular cylinder have equal base and equal height. If the radius of the base and the height are in the ratio 5 : 12, then the ratio of the total surface area of the cylinder to that of the cone is (a) 3 : 1 (b) 13 : 9 (c) 17 : 9 (d) 34 : 9
View Solution
Knowledge Check
A cone has a slant height of 8 and a lateral area of 48π. What is the radius of the base of the cone ?
A3B6C12D16
A cuboid has total surface area of 40m2 and its lateral surface area is 26m2 . Find the area of its base.
View SolutionThe interior of a building is in the form of a cylinder of base radius 12 m and height 3.5 m, surmounted by a cone of equal base and slant height 12.5 m. Find the internal curved surface area and the capacity of the building.
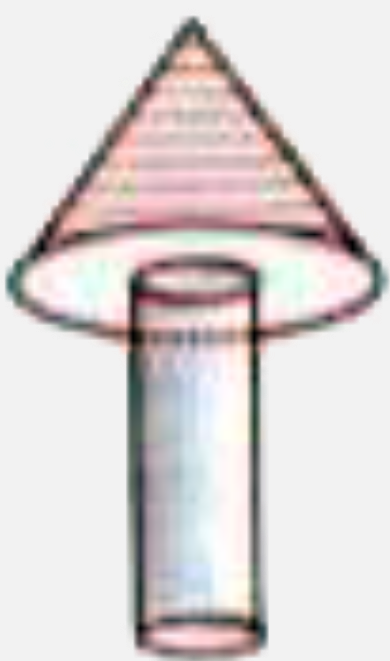
View SolutionA wooden toy is in the shape of a cone mounted on a cylinder as shown alongside.
If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm, find the total surface area of the toy. Take π=3.14]
View SolutionTwo cones with same base radius 8 cm and height 15 cm are joined together along their bases. Find the surface area of the shape so formed.
View SolutionA wooden toy is in the shape of a cone mounted on a cylinder as shown alongside If the height of the cone is 24 cm the total height of the toy is 60 cm and the radius of the base of the cone= twice the radius of the base of the cylinder = 10 cm .Find the total surface area of the you.

View SolutionThe radius and height of a cone are in the ratio 4:3. The area of the base is 154cm2. Find the area of the curved surface.
View SolutionThe radius and height of a cone are in the ratio 4:3. The area of the base is 154cm2. Find the area of the curved surface.
View Solution
