The lengths of the sides of a triangle are 23, 32 , and 37 . To the nearest degree , what is the value of the largest angle ?

A

$71^{\circ}$

B

$83^{\circ}$

C

$122^{\circ}$

D

$128^{\circ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

The angle opposite the 37 side (call it $∠ A$ ) is the largest angle . By the Law of Cosines , $37^{2} = 23^{2} + 32^{2} - 2 (23) (32) cos A .$
$cos A = \frac{37^{2} - 23^{2} - 32^{2}}{- 2 (23) (32)} \approx \frac{- 184}{- 1, 472} = 0.125$ .
Therefore , $A = {cos}^{- 1} (0.125) \approx 83^{\circ}$ .

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The lengths of the triangle shown below are rounded to the nearest 0.1 cm. What is the area, to the nearest $1 c m^{2}$ of the triangle?

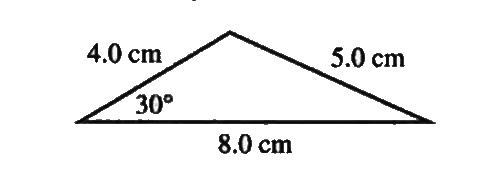
Note: The area of any triangle with sides of length a, b and c opposite angle of measure A, B, and C, respectively, is given by $\frac{1}{2} a b sin C$ .
A4
B5
C8
D10
Question 2 - Select One
The sides of a triangle are in the ratio 4:3:2 . If the perimeter of the triangle is 792, what is the length of the smallest side ?
A176
B200
C264
D352

ENGLISH SAT-MODEL TEST 5-MCQs

Home
Ask Doubt
Profile