A hill, 101(13) m in height, has 14 th of its height under water. What is the height of the hill visible above the water?
To solve the problem step by step, we will follow these calculations:
Step 1: Convert the mixed number to an improper fraction
The height of the hill is given as 10113 meters. We need to convert this mixed number into an improper fraction.
- Calculation:
10113=3×101+13=303+13=3043 meters
Step 2: Determine the fraction of the hill that is underwater
We know that 14 of the hill's height is underwater. To find the height that is underwater, we will multiply the total height by 14.
- Calculation:
Height underwater=14×3043=30412=763 meters
Step 3: Calculate the height of the hill visible above water
To find the height of the hill that is visible above water, we subtract the height underwater from the total height of the hill.
- Calculation:
Height above water=Total height−Height underwater
=3043−763=304−763=2283 meters
Step 4: Simplify the height above water
Now, we simplify 2283.
- Calculation:
2283=76 meters
Final Answer
The height of the hill visible above the water is 76 meters.
---
The height of the hill is given as 10113 meters. We need to convert this mixed number into an improper fraction.
10113=3×101+13=303+13=3043 meters
We know that 14 of the hill's height is underwater. To find the height that is underwater, we will multiply the total height by 14.
Height underwater=14×3043=30412=763 meters
To find the height of the hill that is visible above water, we subtract the height underwater from the total height of the hill.
Height above water=Total height−Height underwater
=3043−763=304−763=2283 meters
Now, we simplify 2283.
2283=76 meters
The height of the hill visible above the water is 76 meters.
Topper's Solved these Questions
- FRACTIONS AND DECIMALSBOOK - NCERT EXEMPLARCHAPTER - FRACTIONS AND DECIMALSEXERCISE - EXERCISE (FIND THE ERROR)
3 Videos
- FRACTIONS AND DECIMALSBOOK - NCERT EXEMPLARCHAPTER - FRACTIONS AND DECIMALSEXERCISE - THINK AND DISCUSS
9 Videos
- EXPONENTS AND POWERSBOOK - NCERT EXEMPLARCHAPTER - EXPONENTS AND POWERSEXERCISE - EXERCISE
136 Videos
- INTEGERSBOOK - NCERT EXEMPLARCHAPTER - INTEGERSEXERCISE - VOCOBULARY
5 Videos
Similar Questions
A submarine 934 metres in height is floating on water.If 13 of its height is under water,then what is the height of the submarine visible above water?
View SolutionWater is filled in a tank upto 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
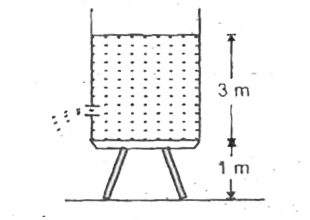
View Solution
Knowledge Check
Water is filled in tank 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
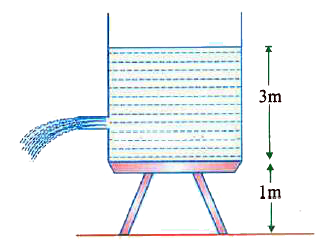 A3 m from groundB1 m from groundC4 m from groundD2 m from ground
A3 m from groundB1 m from groundC4 m from groundD2 m from groundThe top of a hill when observed from the top and bottom of a building of height h is at angles of elevation P and q respectively. What is the height of the hill ?
Ahcotqcotq−cotpBhcotpcotP−cotqC2htanptanp−tanqD2htanqtanq−tanpThe angle of elevation of a cloud from a height h above the level of water in a lake is α and the angle of depressionof its image in the lake is β. Find the height of the cloud above the surface of the lake:
AhcotβBh(cotα+cotβ)ChcotαDh(cotα+cotβcotα−cotβ)
A block flats in water at 40C so that 0.984 of its height is under water. At what temperature of water will the block just sink in water? Negleact expansion of block.
(γRfor water=2.1×10−4/0C)
View SolutionA cylindrical pot is slowly filled with. water. The centre of mass of the empty pot is at a height of 10cm, the mass of the pot is 1kg, and its inner area is 0.4m2. What is the height (in cm ) of the water in it, if the centre of mass of the system is at the lowest position? (Take density of water 1000kgm3 .
View SolutionA ball is dropped from a height 64 m above the ground and every time it hits the ground it rises to a height equal to half of the previous. What is the height attained after it hits the ground for the 16th time?
View SolutionThe top of a hill when observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. What is the height of the hill?
View SolutionA fish in water sees an object which is 24cm above the surface of water. The height of the object above the surface of water that will appear to the flash is (μ=4/3)
View Solution
