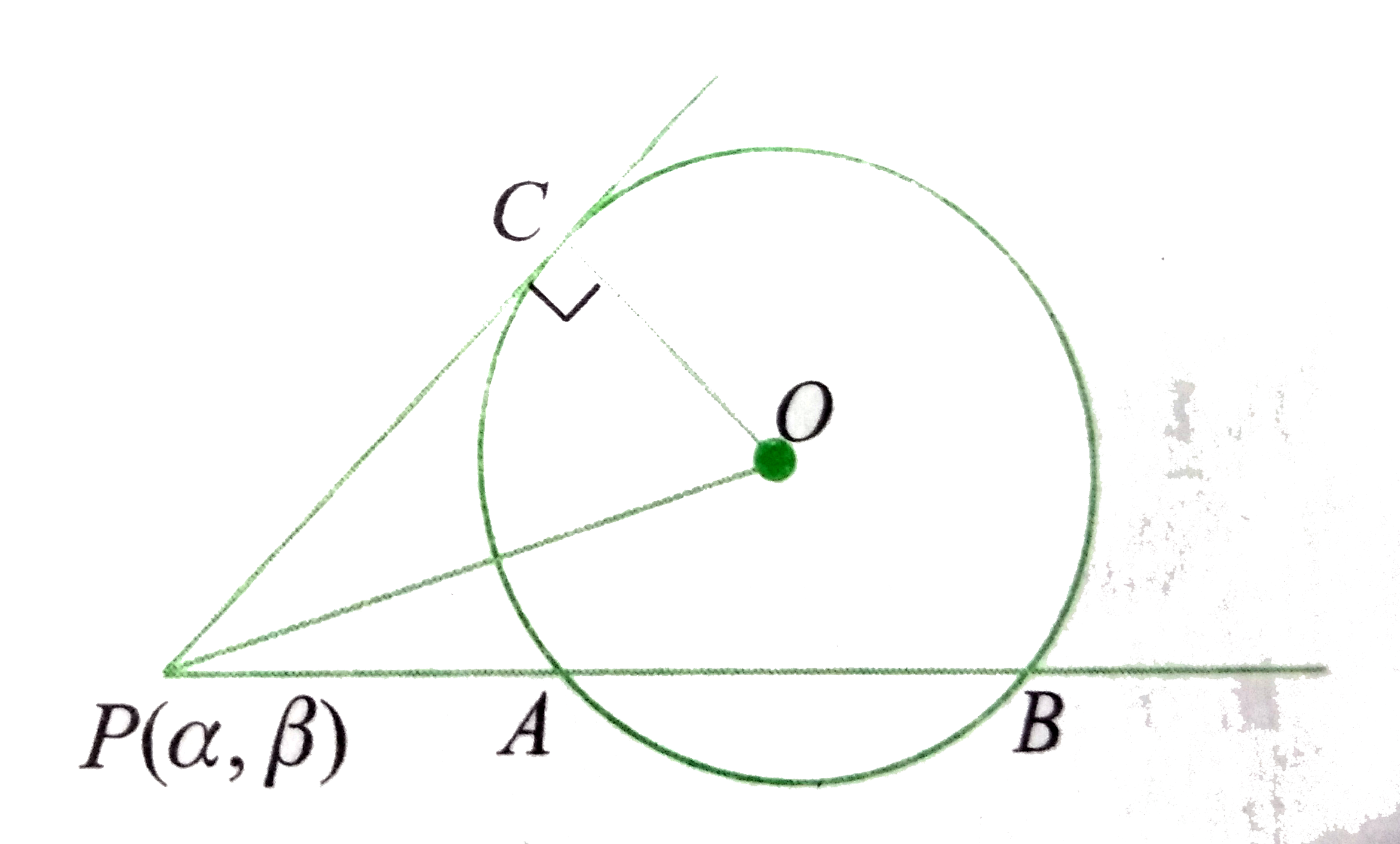
A line is drawn through a fix point P(α,β) to cut the circle x2+y2=r2 at A and B. Then PA.PB is equal to :
From the figure,
PA.PB= Constant
Also, PA.PB=PC2
But PC2=OP2−OC2
=α2+β2−a2
Hence, PA.PB=α2+β2−a2
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Examples
13 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.1
1 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
A line is drawn through the point P(3,11) to cut the circle x2+y2=9 at A and B. Then PA.PB is equal to
View SolutionIf a line is drawn through a point A(3,4) to cut the circle x2+y2=4 at P and Q then AP .AQ=
View SolutionThe tangent at the point (α,β) to the circle x2+y2=r2 cuts the axes of coordinates in AandB. Prove that the area of the triangle OAB is a2r4|αβ|,O being the origin.
View SolutionIf a line passes through the point P(1,−2) and cuts the x2+y2−x−y=0at A and B, then themaxiμmofPA+PB is
View SolutionIf (1+ax)n=1+8x+24x2+… and a line through P(a,n) cuts the circle x2+y2=4 in AandB, then PA.PB=
View SolutionLet normals to the parabola y2=4x at variable points P(t21,2t1)andQ(t22,2t2) meet at the point R(t22t), then the line joining P and Q always passes through a fixed point (α,β), then the value of |α+β| is equal to
View SolutionI If a point (α,β) lies on the circle x2+y2=1 then the locus of the point (3α.+2,β), is
View SolutionIf a circle passes through the point (a,b) and cuts the circlex x2+y2=p2 equation of the locus of its centre is
View SolutionComprehension (Q.6 to 8) A line is drawn through the point P(−1,2) meets the hyperbola xy=c2 at the points A and B (Points A and B lie on the same side of P) and Q is a point on the lien segment AB. If the point Q is choosen such that PQ, PQ and PB are inAP, then locus of point Q is x+y(1+2x) (b) x=y(1+x) 2x=y(1+2x) (d) 2x=y(1+x)
View SolutionThrough a fixed point (h, k) secants are drawn to the circle x2+y2=r2. Then the locus of the mid-points of the secants by the circle is
View Solution
