A line is parallel to XY- plane if all the points on the line have equal …………..
To determine the condition for a line to be parallel to the XY-plane, we need to analyze the coordinates of points on the line.
1. Understanding the XY-plane: The XY-plane is defined by the coordinates (x, y, z) where the z-coordinate is always zero. This means that any point on the XY-plane can be represented as (x, y, 0).
2. Condition for Parallelism: A line is said to be parallel to the XY-plane if it does not change in the z-direction as it moves along the x and y directions. This means that the z-coordinate remains constant for all points on the line.
3. Identifying the Z-coordinate: If we denote the points on the line as (x1, y1, z1), (x2, y2, z2), (x3, y3, z3), etc., for the line to be parallel to the XY-plane, it must hold that:
- z1 = z2 = z3 = ... = constant.
4. Conclusion: Therefore, if all points on the line have equal z-coordinates, it confirms that the line is parallel to the XY-plane.
Final Answer:
A line is parallel to the XY-plane if all the points on the line have equal Z-coordinates.
---
- z1 = z2 = z3 = ... = constant.
A line is parallel to the XY-plane if all the points on the line have equal Z-coordinates.
Topper's Solved these Questions
- INTRODUCTION TO THREE DIMENSIONAL GEOMETRYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - Objective type Questions
13 Videos
- CONIC SECTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - Objective type
13 Videos
- LIMITS AND DERIVATIVES BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LIMITS AND DERIVATIVES EXERCISE - FILLERS
4 Videos
Similar Questions
A line is parallel to YZ-plane, if all the points on the
line have equal
View SolutionA line is parallel to X-axis,if all the points on the line have equal………..
View SolutionStatement-1 line x−13=y−211=z+111 lies in the plane 11x−3z−14=0 .
Statement-2 A straight line lies in a plane, if the line is parallel to plane and a point of the line in the plane.
View SolutionShow that the relation "is parallel to" on the set S of all straight lines in a plane is an equivalence relation.
View SolutionIf there are nine straight lines of which five are concurrent at a point and the other four are concurrent at another point and no two of these nine lines are parallel, then the number of points of intersection is equal to
View SolutionWhere line XY is parallel to line QU.
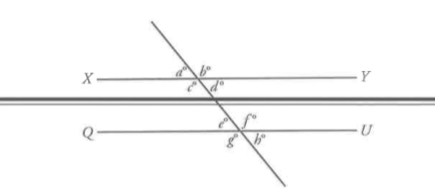
If a+e=150, find f.
View SolutionLet R be a relation on the set of all lines in a plane defined by (l1, l2)∈R <=> line l1 is parallel to line l2 . Show that R is an equivalence relation.
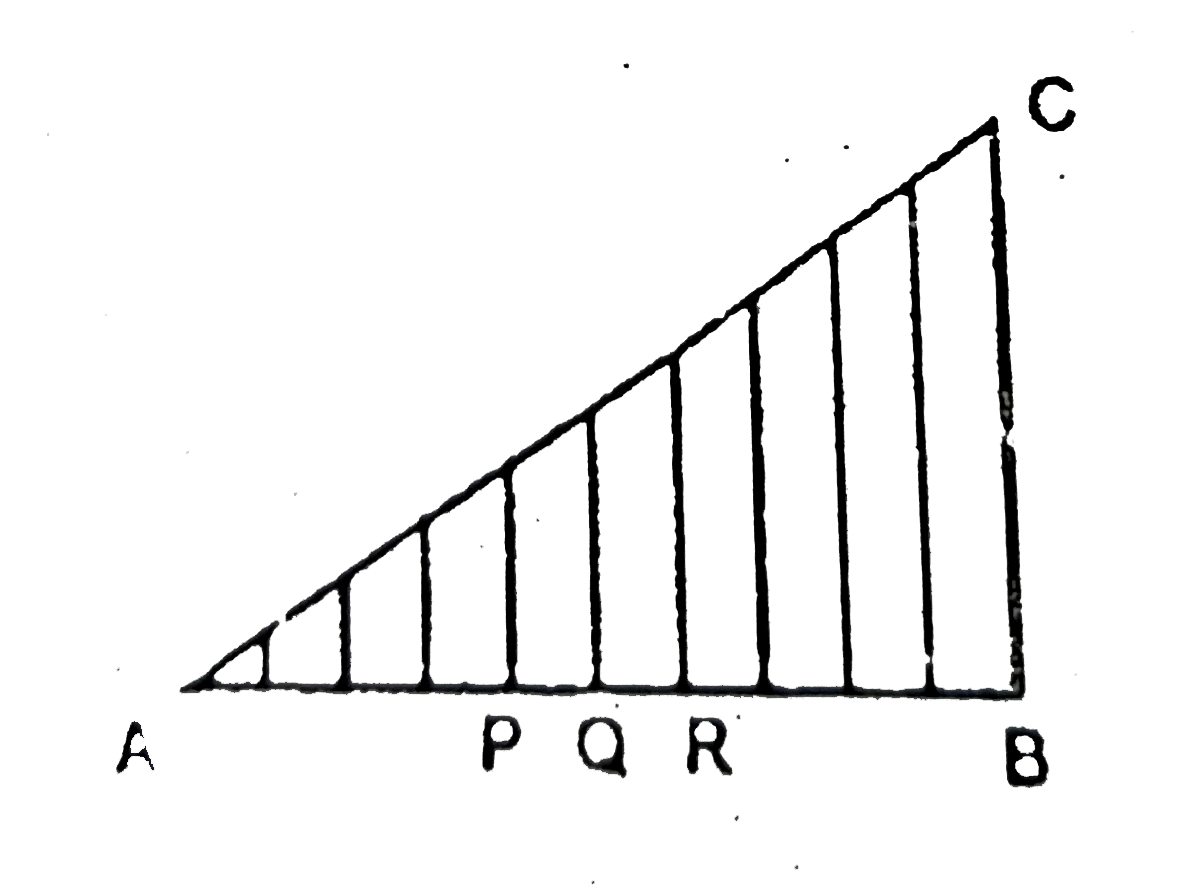
View SolutionThere are infinite equipotential lines all parallel to BC in a right angled triangular region ABC as shown in the figure. All the points on a line have the same potential proportional to the length of the line.
If EP, EQ & ER denote the electric field at P, Q and R, respectively, then
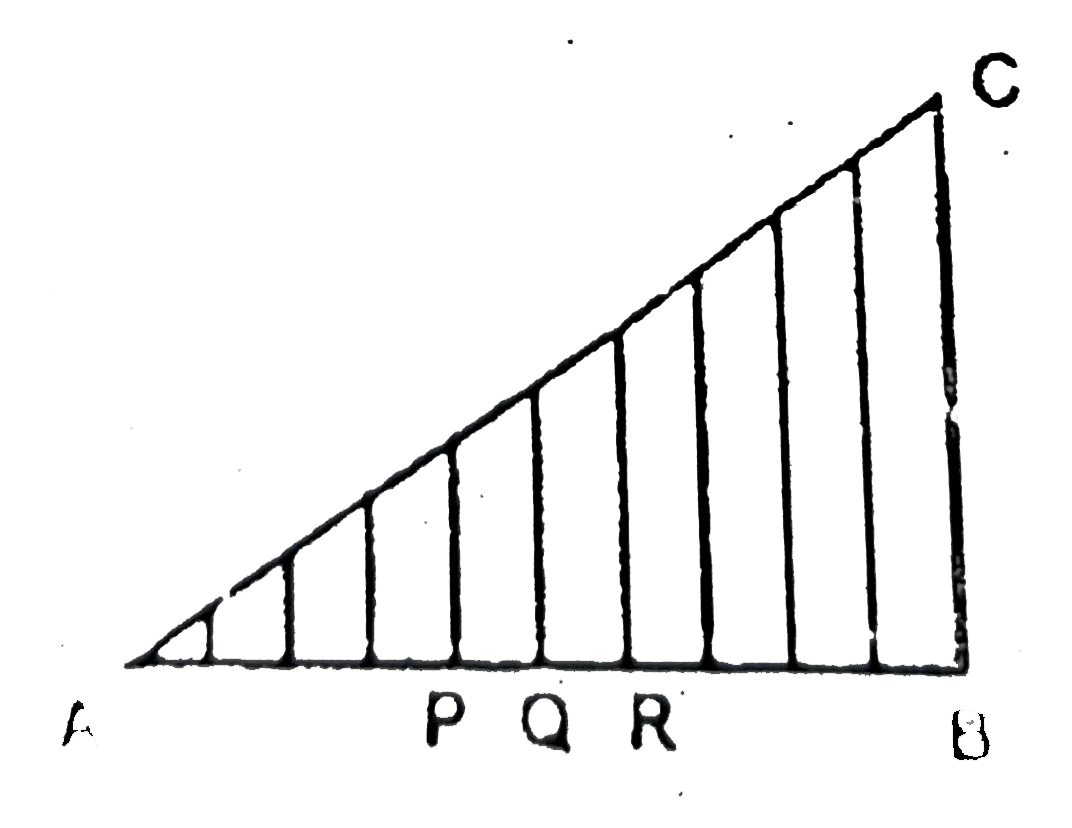
View SolutionThere are infinite equipotential lines all parallel to BC in a right angled triangular region ABC as shown in the figure. All the points on a line have the same potential proportional to the length of the line.
A positive charge is moved from A to B and C separately to do work. WA→B & WA→C, respectively, then
View SolutionThere are infinite equipotential lines all parallel to BC in a right angled triangular region ABC as shown in the figure. All the points on a line have the same potential proportional to the length of the line.
A positive charge is moved from A to B and C separately to do work. WA→B & WA→C, respectively, then

View Solution
