A manufacture makes two types of cups A and B. Three machines are required to manufacture the cups and the time in minutes required by each in as given below:

Each machine is available for a maximum period of 6 hours per day. If the profit on each cup A is 75 paisa and on B is 50 paisa, find how many cups of each type should be manufactures to maximise the profit per day.
The correct Answer is:Type A : 4; Type B : 3
Step by step video, text & image solution for A manufacture makes two types of cups A and B. Three machines are required to manufacture the cups and the time in minutes required by each in as given below: Each machine is available for a maximum period of 6 hours per day. If the profit on each cup A is 75 paisa and on B is 50 paisa, find how many cups of each type should be manufactures to maximise the profit per day. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR PROGRAMMING BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINEAR PROGRAMMING EXERCISE - ONE MARKS QUESTIONS
8 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - 4 MARK QUESTIONS
31 Videos
- MATRICES AND DETERMINANTSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - MATRICES AND DETERMINANTSEXERCISE - SIX MARK QUESTIONS
20 Videos
Similar Questions
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the tune (in minutes) required for each toy on the machines is given below:Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs 7.50 and that on each toy of type B is Rs 5. show that 15 toys of type A and 30 of the B should be manufactured m a day to get maximum profit.
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each purpose and the time (in minutes) required for each toy on the machines is given below:
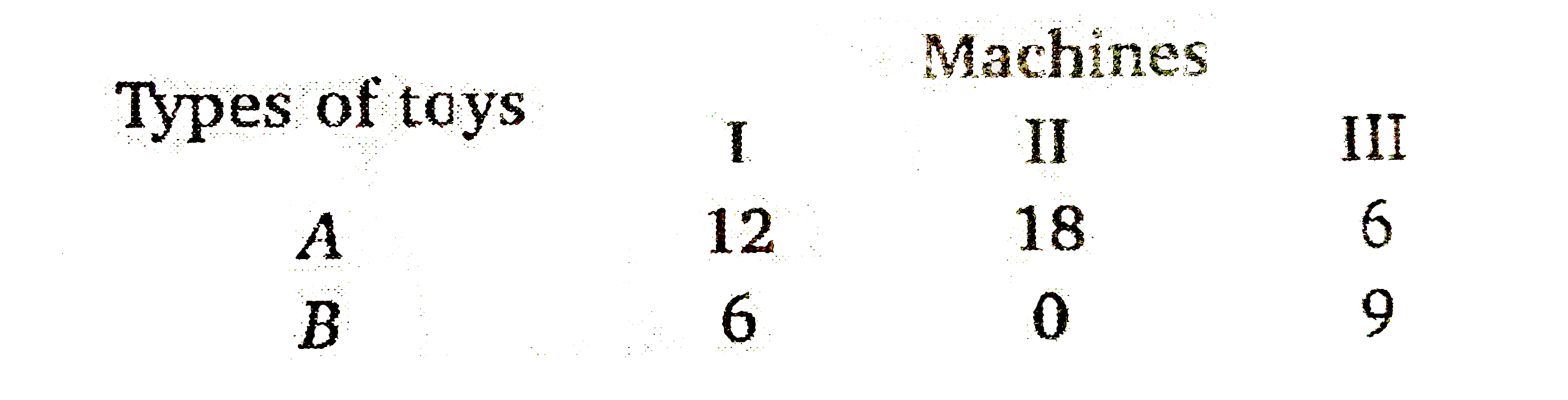
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs. 7.50 and that on each toy of type B is Rs. 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
View SolutionA manufacturer makes two types of toys A and B.Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:

The machine I, II and III are available for a maximum of 3 hours, 2 hours and 2 hours 30 minutes respectively.The profit on each toy of type A is ₹ 50 and that of type B is ₹ 60.Formulate the above problem as a LPP and solve graphically to maximize profit.
View SolutionA small firm manufactures items A and B. The total number of items that it can manufacture in a day is at the most 24 Item A takes on hour to make while item B takes only half an hour. The maximum time available per day is 16 hours. If the profit on one unit of item A be 300 and that on one unit of item B be 160, how many of each type of item should be produced to maximize the profit? Solve the problem graphically
View SolutionA copany manufactures two types of toys, A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is Rs.50 each on type A and Rs.60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit?
View SolutionA company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours for assembling. The profit is Rs 5 each for type A and Rs 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture m order to maximise the profit?
View SolutionA company manufacturers two types of novelty suouvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours for assembling. The profit is Rs. 5 each for type A and Rs. 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximise the profit?
View SolutionA company manufacturers two types of products P and Q. The product P requires 5 minutes each for cutting and 10 minutes each for assembling. The product Q requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes availabe for cutting and 4 hours for assembling. The profit is 50 paise each for type P and 60 paise each for type Q. How many products of each type should the company manufacture in order to maximize the profit?
View SolutionA company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. He earns a profit of Rs.50 each on type A and Rs.60 each on type. B. How many toys of each type should the company manufacture in a day to maximize the profit ?
View SolutionIn a small scale industry, a manufacturer produces two types of book cases. The first type of book case requires 3 hours on machine A and 2 hours on machine B for completion whereas the second type of book case requires 3 hours on machine A and 3 hours on machine B. The machines A and B respectively run for at the most 18 hours and 14 hours per day. He earns a profit of 30 on each type of case of first type and 40 on each book case of second type. How many book cases of each type should he manufacture so as to have maximum profit. Make it an LPP and solve it graphically.
View Solution
