A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each purpose and the time (in minutes) required for each toy on the machines is given below:
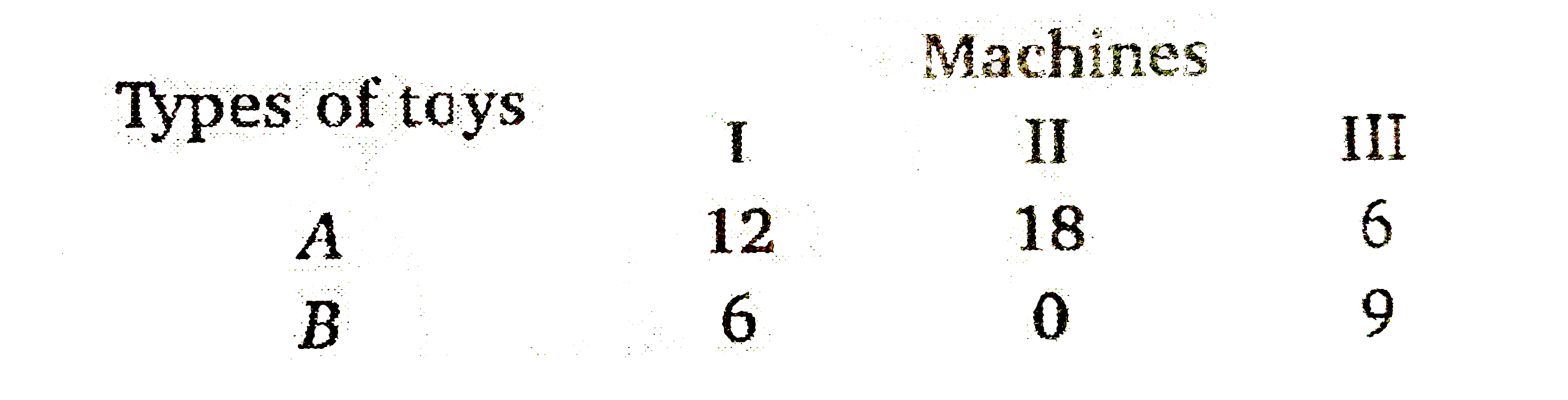
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs. 7.50 and that on each toy of type B is Rs. 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
Let the manufacturer produces x toys of type A and y toys of type B. Then
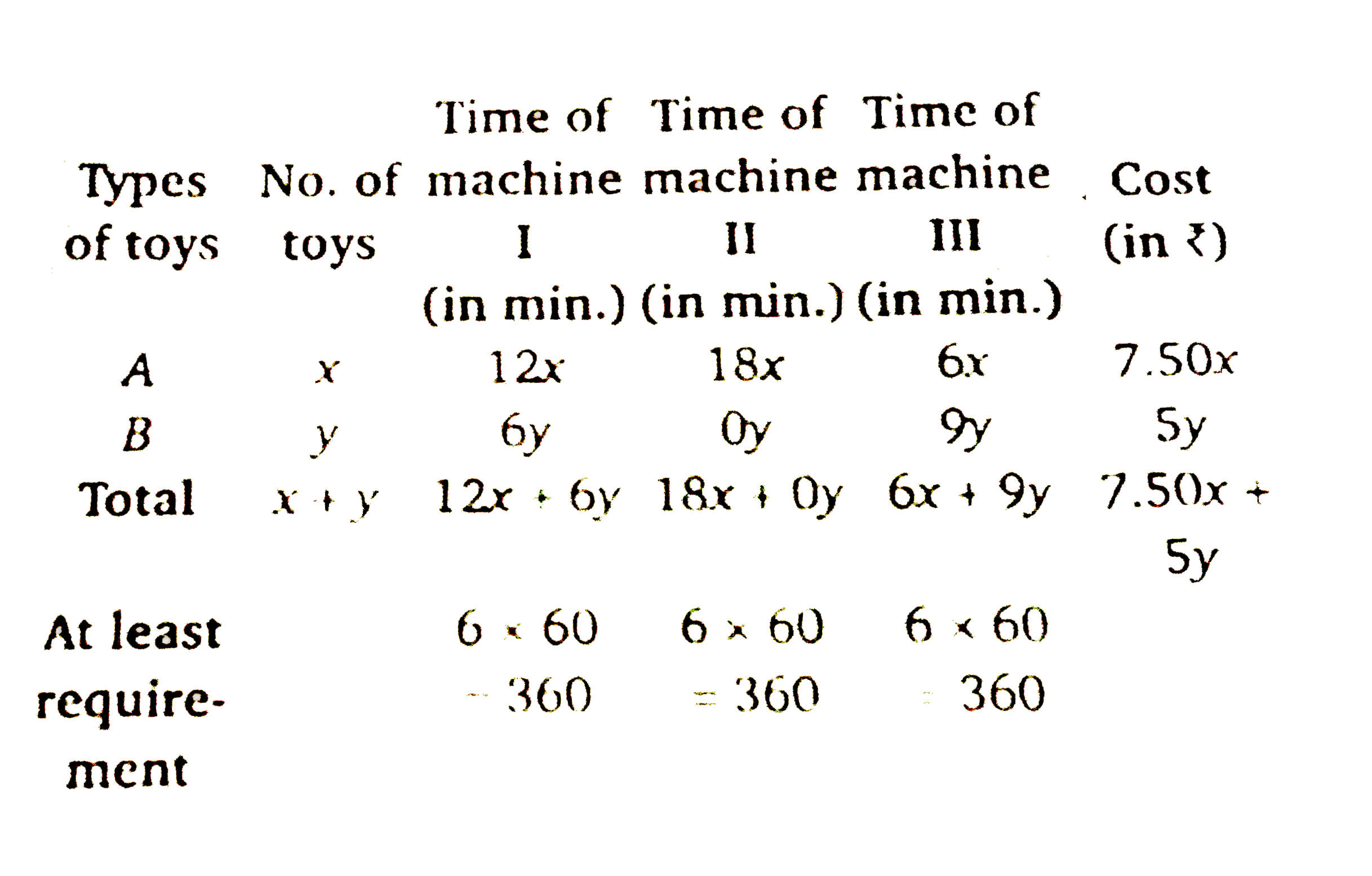
Maximise Z=7.50x+5y……………1
and constraints
12x+6y≥360⇒2x+y≤60…………2
18x≤360⇒x≤20…………….3
6x+9y≤360⇒2x+3y≤120.............4
x≥0,y≥0.................5
First, draw the graph of the line 2x+y=60
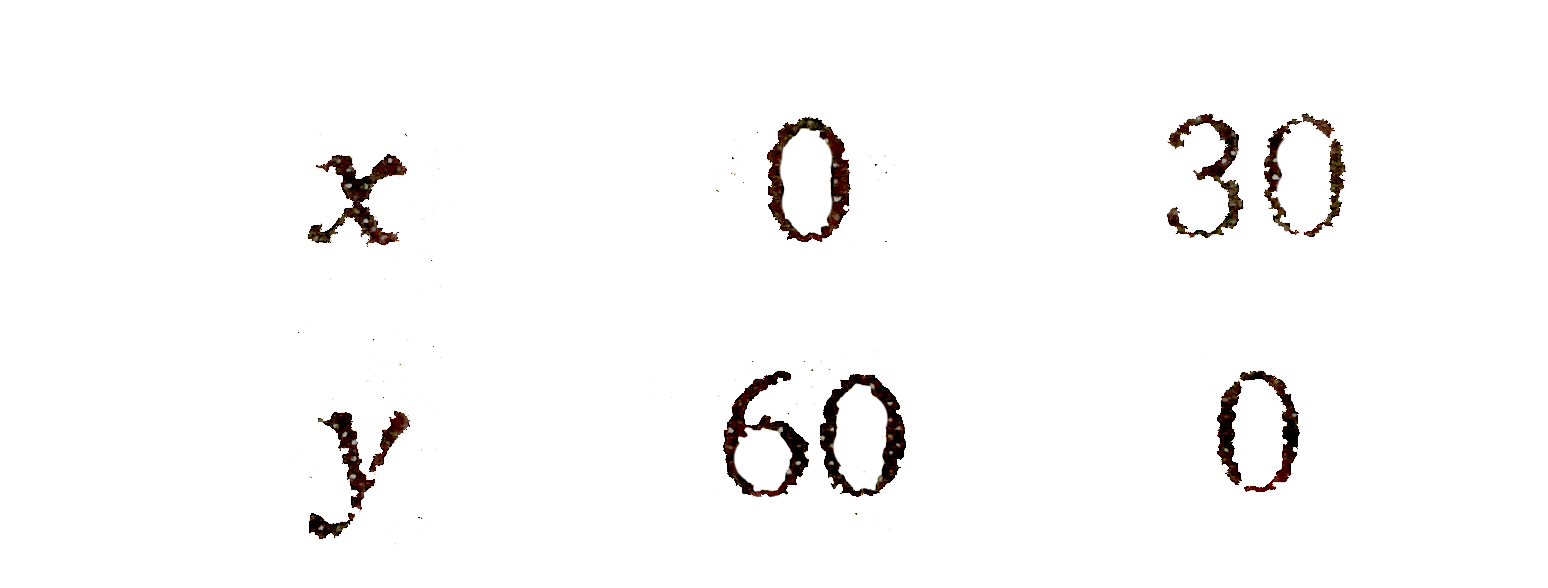
Put (0,0) in the inequation 2x+y≤60
2×0+0≤60⇒0≤60 (True)
Thus, the half plane contains the origin.
Now draw the graph of the line 2x+3y=120
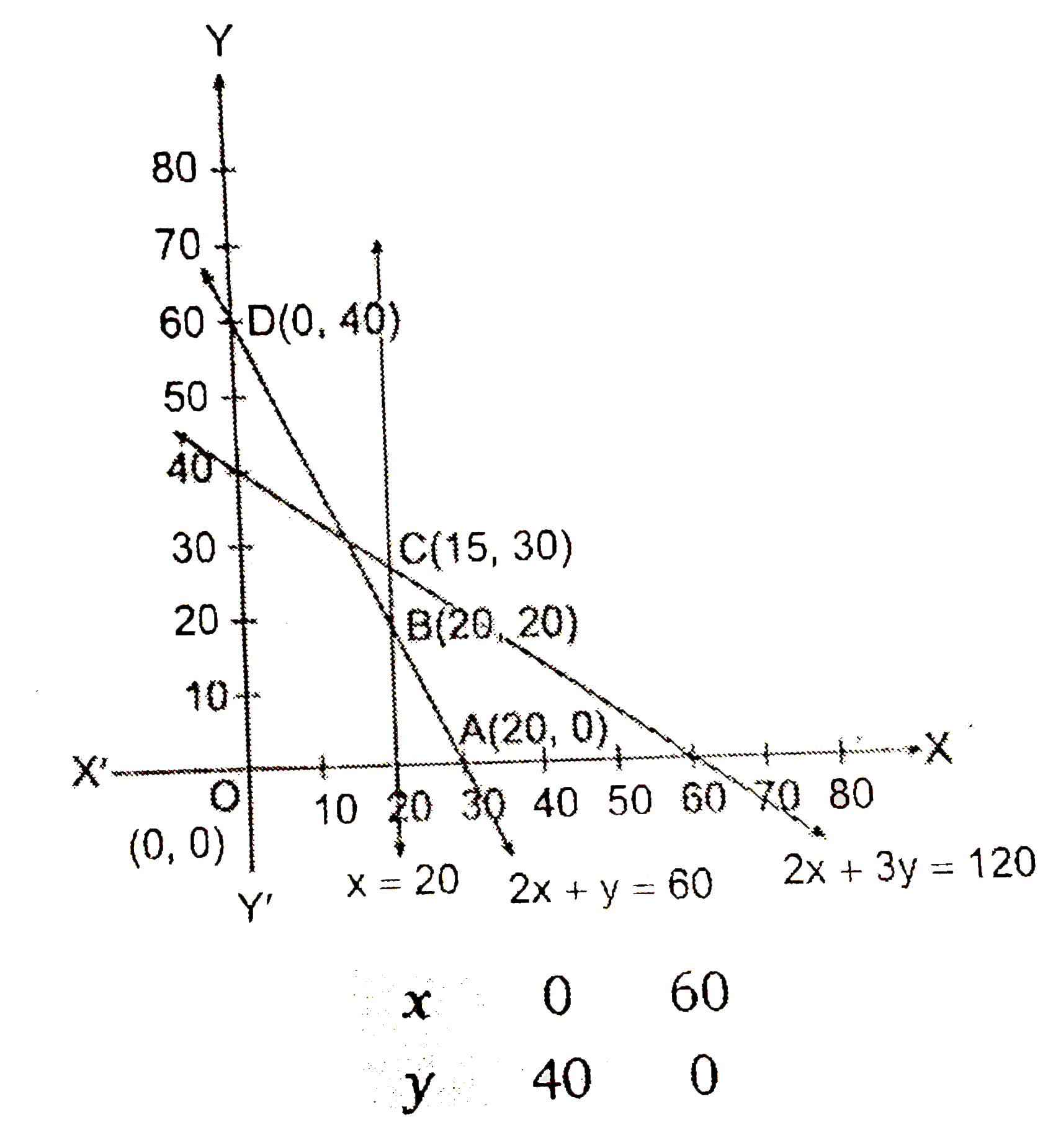
Put (0,0) in the inequation 2x+3y≤120,
2×0+3×0≤120
=0≤120 (True)
Thus, the half plane contains the origin.
Now, draw the graph of theline x=20
Put (0,0) in the inequatioins x≤20,0≤20 (True)
Thus, the half plane contains origin.
Since x,y≥0. So the feasible region will be first quadrant.
The point of intersection of the equations 2x+y=60 and 2x+3y=120 is C(15,30). Similarly, the pont of intersection of the equation x=20 and 2x+y=60 is B(20,20). Thus, the feasible region is OABCDO.
The vertices of feasible region are A(20,0),B(20,20),C(15,30) and D(0,40). We find the value of Z at these vertices.
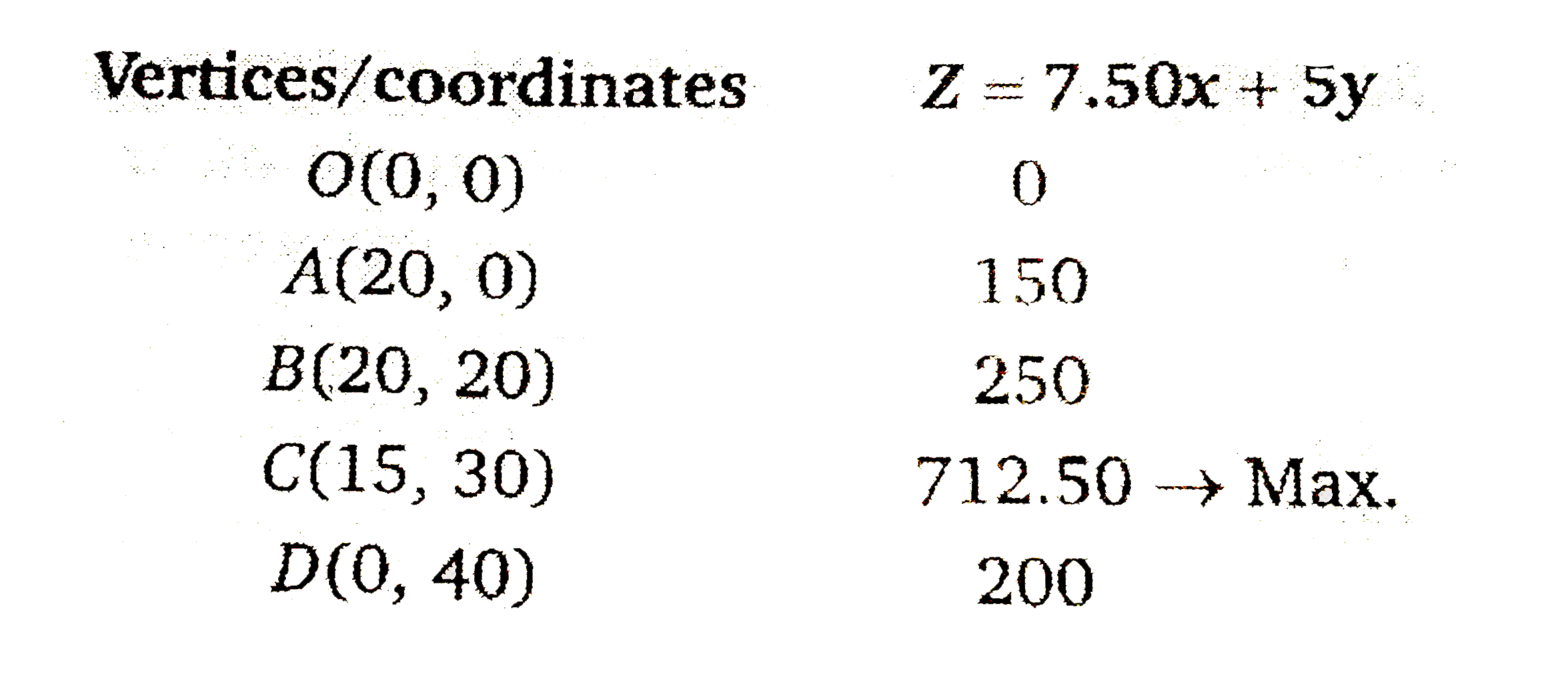
Thus, the maximum value of Z is Rs. 712.50 at point C(15,30). Therefore to obtain the maximum cost Rs. 712.50, he makes 15 toys of type A and 30 toys of type B.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBook:NAGEEN PRAKASHANChapter:LINEAR PROGRAMMINGExercise:Exercise 12.2
Explore 11 Videos
- INVERES TRIGONOMETRIC FUNCTIONSBook:NAGEEN PRAKASHANChapter:INVERES TRIGONOMETRIC FUNCTIONSExercise:Miscellaneous Exercise (prove That )
Explore 9 Videos
- MATRICESBook:NAGEEN PRAKASHANChapter:MATRICESExercise:Miscellaneous Exerice
Explore 15 Videos
Similar Questions
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the tune (in minutes) required for each toy on the machines is given below:Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs 7.50 and that on each toy of type B is Rs 5. show that 15 toys of type A and 30 of the B should be manufactured m a day to get maximum profit.
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the tune (in minutes) required for each toy on the machines is given below:
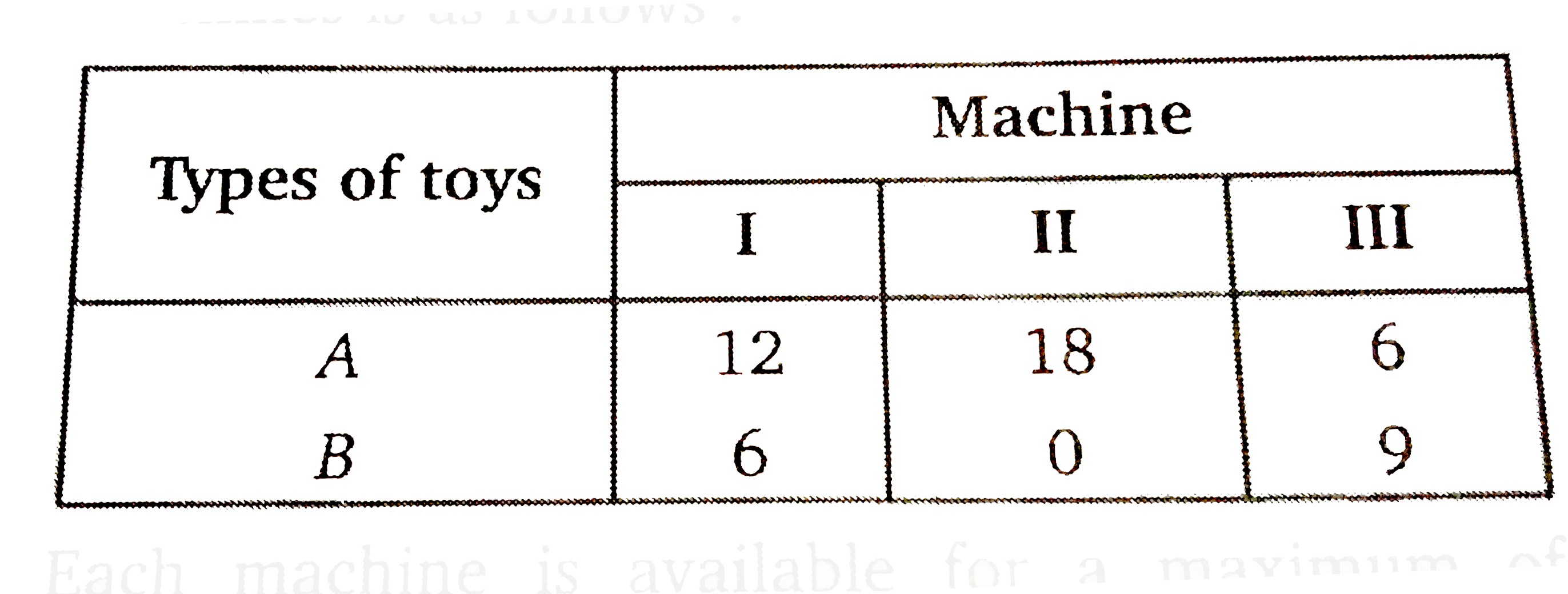 Each machine is available for a
maximum of 6 hours per day. If the profit
Each machine is available for a
maximum of 6 hours per day. If the profit
View SolutionA manufacturer manufactures two types of tea-cups, A and B. Three machines are needed for manufacturing the tea cups. The time in minutes required for manufacturing each cup on the machines is given below:
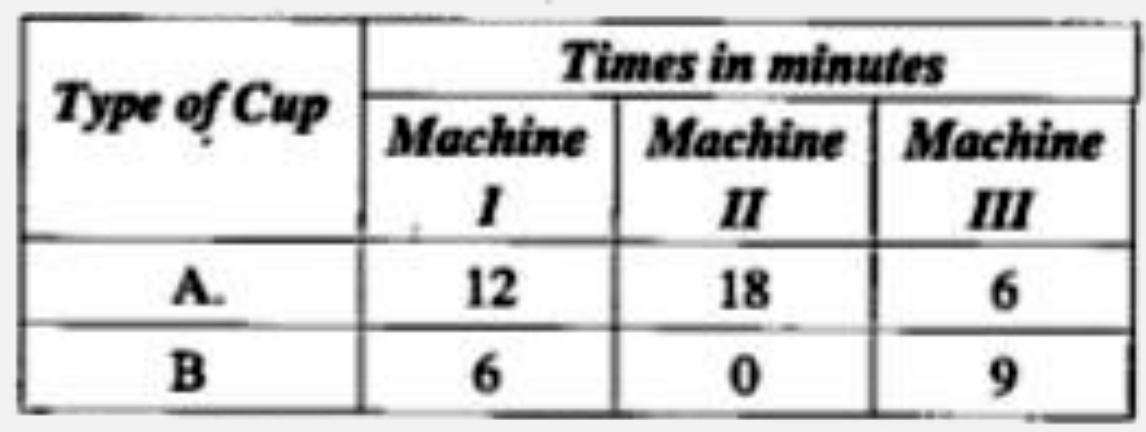
Each machine is available for a maximum of six hours per day. If the profit on each cup of type A is Rs 1.50and that'on each cup of type B is Rs 1.00, find the number of cups of each type that should be manufactured in a day to get maximumprofit.
View SolutionA manufacturer makes two types of toys A and B.Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:

The machine I, II and III are available for a maximum of 3 hours, 2 hours and 2 hours 30 minutes respectively.The profit on each toy of type A is ₹ 50 and that of type B is ₹ 60.Formulate the above problem as a LPP and solve graphically to maximize profit.
View SolutionA manufacture makes two types of cups A and B. Three machines are required to manufacture the cups and the time in minutes required by each in as given below:

Each machine is available for a maximum period of 6 hours per day. If the profit on each cup A is 75 paisa and on B is 50 paisa, find how many cups of each type should be manufactures to maximise the profit per day.
View SolutionA company manufactures two types of toys A and B. A toy of type A requires 5 minute for cutting and 10 minute for assembling. A toy of type B requires 8 minute for cutting and 8 minutes for assembling. There are 3 hours available for cutting and 4 hours available for assembling th etoys in a day. The profit is Rs 50 each on a toy of Type A and Rs 60 each on a toy of type B. How many toys of each type should the company manufacture in a day to maximize the profit ? Use linear programming to find the solution.
View SolutionA company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. He earns a profit of Rs.50 each on type A and Rs.60 each on type. B. How many toys of each type should the company manufacture in a day to maximize the profit ?
View SolutionA copany manufactures two types of toys, A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is Rs.50 each on type A and Rs.60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit?
View SolutionA company manufacturers two types of products P and Q. The product P requires 5 minutes each for cutting and 10 minutes each for assembling. The product Q requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes availabe for cutting and 4 hours for assembling. The profit is 50 paise each for type P and 60 paise each for type Q. How many products of each type should the company manufacture in order to maximize the profit?
View SolutionA company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours for assembling. The profit is Rs 5 each for type A and Rs 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture m order to maximise the profit?
View Solution
