A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the tune (in minutes) required for each toy on the machines is given below: Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs 7.50 and that on each toy of type B is Rs 5. show that 15 toys of type A and 30 of the B should be manufactured m a day to get maximum profit.
Let x and y toys of type A and B severally be factory-made in an exceedingly day.
The given drawback may be developed as follows:
Maximisez=7.5x+5y
subject to the constraints
2x+y≤60
x≤20
2x+3y≤120
x,y≥0
The possible region determined by the constraints is as shown
The corner points of the possible region are A(20,0),B(20,20),C(15,30)andD(0,40)
The value of z at these corner points are as follows.
so,The maximum value of z is 262.5 at (15,30)
Thus, the manufacturer should manufacture 15 toys of type A and 30 toys of type B to maximize the profit.
Topper's Solved these Questions
Similar Questions
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each purpose and the time (in minutes) required for each toy on the machines is given below:
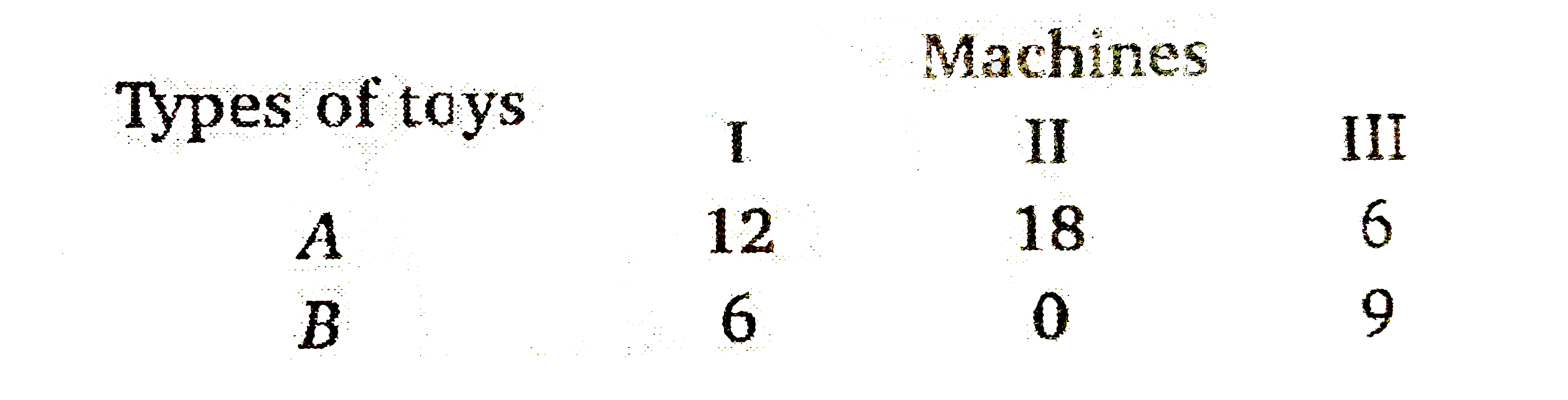
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs. 7.50 and that on each toy of type B is Rs. 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
View SolutionA manufacturer makes two types of toys A and B.Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:

The machine I, II and III are available for a maximum of 3 hours, 2 hours and 2 hours 30 minutes respectively.The profit on each toy of type A is ₹ 50 and that of type B is ₹ 60.Formulate the above problem as a LPP and solve graphically to maximize profit.
View Solution
Knowledge Check
The cost of 24 toys of the same kind is Rs 783.60. Find the cost of each toy.
A31.65B32.00C32.65D30.65A manufacturer produces two types of soaps using two machines A and B . A is operated for 2 minutes and B for 3 minutes to manufacture first type , while it takes 3 minutes on machine A and 5 minutes on machine B to manufature second type . Each machine can be operated at the most for 8 hours per day . The two types of soap are sold at a profit of Rs 0.25 and Rs 0.05 each respectively . Assuming that the manufactured can sell all the soaps he can manufacture , how many soaps of each type should be manufature per day so as to maximize his profit .
A50 soaps of type I , 20 soaps of types IIB96 soaps of type IIC45 soaps of type ID55 soaps of type I
A manufacture makes two types of cups A and B. Three machines are required to manufacture the cups and the time in minutes required by each in as given below:

Each machine is available for a maximum period of 6 hours per day. If the profit on each cup A is 75 paisa and on B is 50 paisa, find how many cups of each type should be manufactures to maximise the profit per day.
View SolutionA company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. He earns a profit of Rs.50 each on type A and Rs.60 each on type. B. How many toys of each type should the company manufacture in a day to maximize the profit ?
View SolutionA copany manufactures two types of toys, A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is Rs.50 each on type A and Rs.60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit?
View SolutionIn a small scale industry, a manufacturer produces two types of book cases. The first type of book case requires 3 hours on machine A and 2 hours on machine B for completion whereas the second type of book case requires 3 hours on machine A and 3 hours on machine B. The machines A and B respectively run for at the most 18 hours and 14 hours per day. He earns a profit of 30 on each type of case of first type and 40 on each book case of second type. How many book cases of each type should he manufacture so as to have maximum profit. Make it an LPP and solve it graphically.
View SolutionIf the cost of 9 toys is Rs 333.find the cost of one toy
View SolutionA company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours for assembling. The profit is Rs 5 each for type A and Rs 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture m order to maximise the profit?
View Solution
