A parallelogram has two sides 60 m and 25 m and a diagonal 65 m long. The area of the parallelogram is :
1000 m2
1400 m2
1600 m2
1500 m2
The correct Answer is:D
To find the area of the parallelogram with sides of lengths 60 m and 25 m, and a diagonal of length 65 m, we can use Heron's formula to first find the area of triangle ACD formed by the diagonal. The area of the parallelogram will then be double that area.
1. Identify the sides of triangle ACD:
- The sides are given as:
- AC = 60 m
- AD = 25 m
- CD (the diagonal) = 65 m
2. Calculate the semi-perimeter (s):
s=AC+AD+CD2=60+25+652=1502=75 m
3. Apply Heron's formula:
- Heron's formula states that the area (A) of a triangle can be calculated using:
A=√s(s−a)(s−b)(s−c)
- Here, a=60m, b=25m, c=65m.
4. Substitute the values into Heron's formula:
A=√75(75−60)(75−25)(75−65)
A=√75(15)(50)(10)
5. Calculate the individual terms:
- First, calculate 75×15=1125
- Next, calculate 1125×50=56250
- Finally, calculate 56250×10=562500
6. Find the square root:
A=√562500=750 m2
7. Calculate the area of the parallelogram:
- The area of the parallelogram is double the area of triangle ACD:
Area of parallelogram=2×A=2×750=1500 m2
Final Answer:
The area of the parallelogram is 1500 m².
- The sides are given as:
- AC = 60 m
- AD = 25 m
- CD (the diagonal) = 65 m
s=AC+AD+CD2=60+25+652=1502=75 m
- Heron's formula states that the area (A) of a triangle can be calculated using:
A=√s(s−a)(s−b)(s−c)
- Here, a=60m, b=25m, c=65m.
A=√75(75−60)(75−25)(75−65)
A=√75(15)(50)(10)
- First, calculate 75×15=1125
- Next, calculate 1125×50=56250
- Finally, calculate 56250×10=562500
A=√562500=750 m2
- The area of the parallelogram is double the area of triangle ACD:
Area of parallelogram=2×A=2×750=1500 m2
The area of the parallelogram is 1500 m².
Topper's Solved these Questions
- PERIMETER AND AREA BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PERIMETER AND AREA EXERCISE - QUESTION BANK - 21(C)
10 Videos
- PERCENTAGE AND ITS APPLICATIONSBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PERCENTAGE AND ITS APPLICATIONSEXERCISE - Self Assessment Sheet - 10
10 Videos
- POLYGONS AND QUADRILATERALSBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POLYGONS AND QUADRILATERALSEXERCISE - Self Assessment Sheet
10 Videos
Similar Questions
Knowledge Check
ABCD is a parallelogram with sides AB = 12 cm, BC= 10 cm and diagonal AC = 16 cm. The area of the parallelogram and the distance between the shorter sides are respectively.
A120.5cm2,12.05cmB119.8cm2,11.98cmC118.71cm2,11.87cmD117.9cm2,11.79cmTwo adjacent sides of a parallelogram are 10 cm and 12 cm. If its one diagonal is 14 cm long, find the area of the parallelogram.
A40√3cm2B49√3cm2C48√6cm2D58√6cm2A parallelogram has sides 30 cm and 20 cm and one of its diagonal is 40 cm long. Then its area is :
A75√5cm2B245cm2C150√15cm2D300cm2
A parallelogram has sides 30m and 14m and one of its diagonals is 40 m long. Then, its area is 168 m2 (b) 336 m2 (c) 372 m2 (d) 480 m2
View SolutionA field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
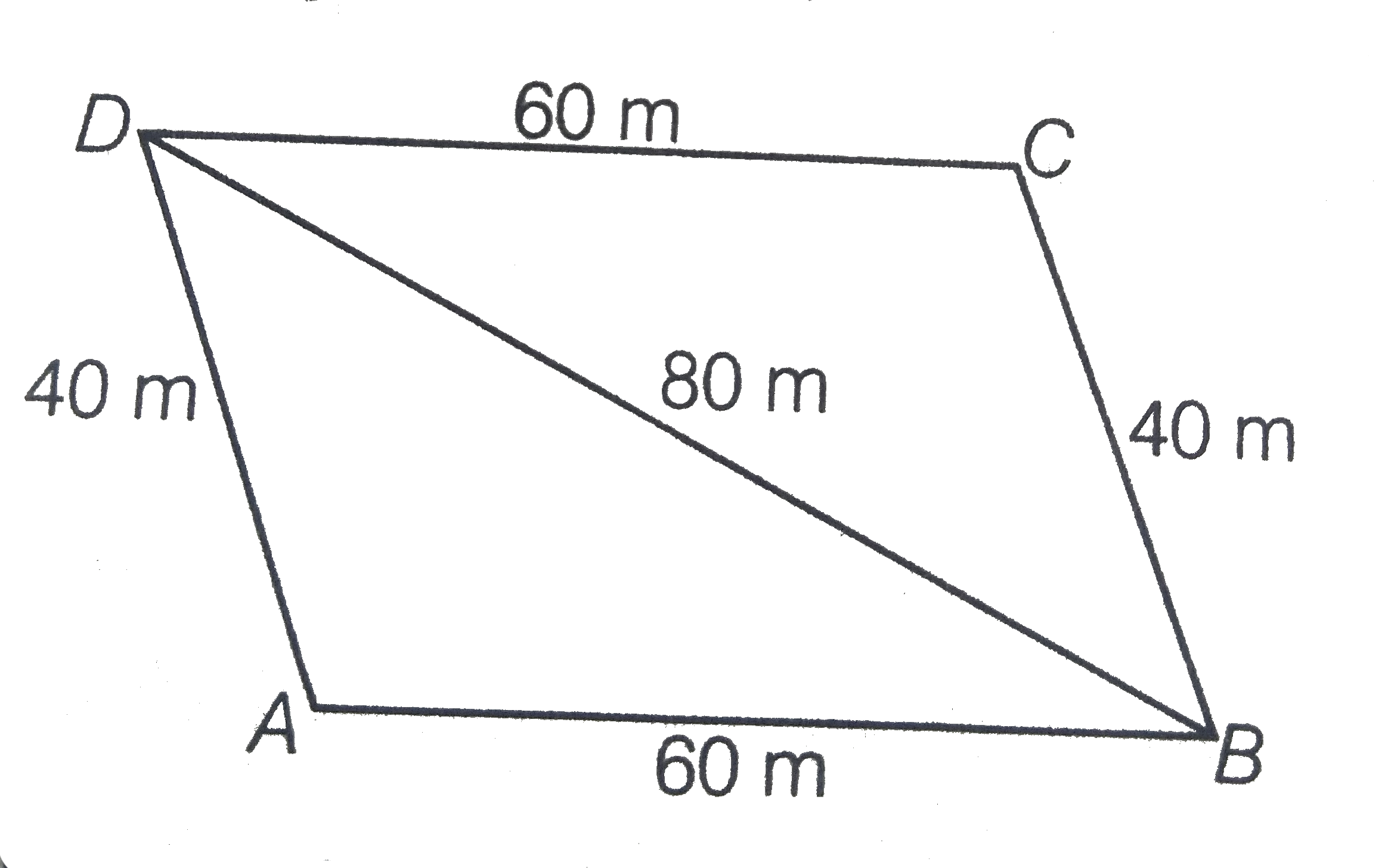
View SolutionA parallelogram has sides 30 m, 70 m and one of its diagonals is 80 m long. Its area will be
View SolutionA parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Its area is.
एक समांतर चतुर्भुज की भुजाएँ 60m और 40m हैं और उसका एक विकर्ण 80m लंबा है। उसका क्षेत्रफल कितना होगा?
View SolutionWhat is the geometric interpretation of the identity (→a−→b)×(→a+→b)=2(→a×→b)?
1. If the diagonals of a given parallelogram are used as sides of a second parallelogram, then the area of the second parallelogram is twice that of the given parallelogram.
2. If the semi-diagonals of a given parallelogram are used as sides of a second parallelogram, then the area of the second parallelogram is half that of the given parallelogram.
Select the correct answer using the code given below
View Solution
