A parallelogram has sides 30m and 14m and one of its diagonals is 40 m long. Then, its area is 168 m2 (b) 336 m2 (c) 372 m2 (d) 480 m2
To find the area of the parallelogram with sides of 30m and 14m, and a diagonal of 40m, we can follow these steps:
Step 1: Identify the sides and diagonal
We have:
- Side AB = 30m
- Side BC = 14m
- Diagonal AC = 40m
Step 2: Calculate the semi-perimeter (s) of triangle ABC
The semi-perimeter (s) is calculated as:
s=AB+BC+AC2=30+14+402=842=42m
Step 3: Apply Heron's formula to find the area of triangle ABC
Heron's formula states that the area (A) of a triangle can be calculated using:
A=√s(s−a)(s−b)(s−c)
where a, b, and c are the lengths of the sides of the triangle.
Substituting the values:
- a=30m
- b=14m
- c=40m
We find:
A=√42(42−30)(42−14)(42−40)=√42×12×28×2
Step 4: Calculate the values inside the square root
Calculating the products:
42×12=504
504×28=14112
14112×2=28224
Step 5: Find the square root
Now we calculate:
A=√28224
Calculating the square root gives:
A=168m2
Step 6: Calculate the area of the parallelogram
The area of the parallelogram is twice the area of triangle ABC:
Area of parallelogram=2×A=2×168=336m2
Conclusion
Thus, the area of the parallelogram is 336m2.
Final Answer
The correct option is (b) 336m2.
---
We have:
- Side AB = 30m
- Side BC = 14m
- Diagonal AC = 40m
The semi-perimeter (s) is calculated as:
s=AB+BC+AC2=30+14+402=842=42m
Heron's formula states that the area (A) of a triangle can be calculated using:
A=√s(s−a)(s−b)(s−c)
where a, b, and c are the lengths of the sides of the triangle.
- a=30m
- b=14m
- c=40m
A=√42(42−30)(42−14)(42−40)=√42×12×28×2
Calculating the products:
42×12=504
504×28=14112
14112×2=28224
Now we calculate:
A=√28224
Calculating the square root gives:
A=168m2
The area of the parallelogram is twice the area of triangle ABC:
Area of parallelogram=2×A=2×168=336m2
Thus, the area of the parallelogram is 336m2.
The correct option is (b) 336m2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
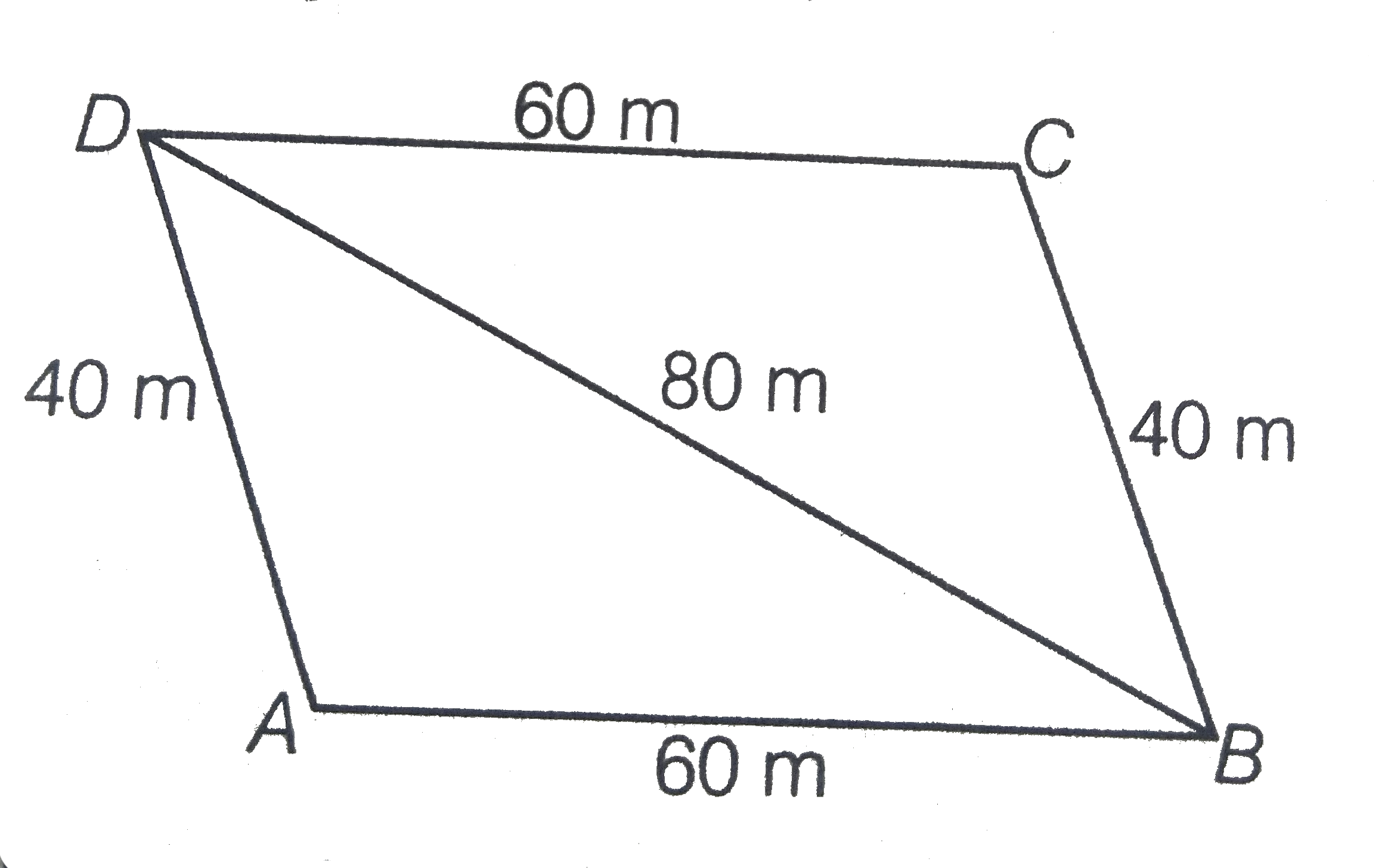 A480 sq. mB320 sq. mC600√15sq.mD450√15 sq . M
A480 sq. mB320 sq. mC600√15sq.mD450√15 sq . MA parallelogram has sides 30 m, 70 m and one of its diagonals is 80 m long. Its area will be
A600 m2B1200√3m2C1200 m2D600√3m2A parallelogram has two sides 60 m and 25 m and a diagonal 65 m long. The area of the parallelogram is :
A1000 m2B1400 m2C1600 m2D1500 m2
One side of a rectangular field is 15 m and one of its diagonals is 17 m. Find the area of the field.
View SolutionThe base of a parallelogram measures 1 m 60 cm and its height is 75 cm. Find its area in m2 .
View SolutionA parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Its area is.
एक समांतर चतुर्भुज की भुजाएँ 60m और 40m हैं और उसका एक विकर्ण 80m लंबा है। उसका क्षेत्रफल कितना होगा?
View SolutionOne side of a rectangular field is 9 m and one of its diagonal is 20 m. Find the area of the field.
View SolutionThe sides of parallelogram are 12 m and 17 m respectively . If one of the diagonals is 25 m long the area of parallelogram is :
A)150m2
B)180m2
C)160m2
D)190m2
View Solution
