A particle falls in a medium whose resistance is propotional to the square of the velocity of the particles. If the differential equation of the free fall is dvdt=g−kv2 (k is constant) then
v=2√gke2t√g/t+1e2r√g/k−1
v=√gke2t√gk−1e2t√gk+1
v→0 as t→∞
v→√gk as t→∞
The correct Answer is:B, D
dvdt=g−kv2
⇒dvg−kv2
⇒⎛⎜
⎜⎝1k∫dv(gk)−v2⎞⎟
⎟⎠=∫(dt+C)
⇒12√gklog∣∣
∣
∣∣√gk+v√g/k−v∣∣
∣
∣∣=t+C
At t=0, v=0 ⇒C=0
⇒v=√gk⎛⎜
⎜
⎜
⎜
⎜⎝1−1e2t√gk1−1e2t√gk⎞⎟
⎟
⎟
⎟
⎟⎠
Clearly when v→√gk as t→∞
Topper's Solved these Questions
- DIFFERENTIAL EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Linked Comprehension types
21 Videos
- DIFFERENTIAL EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Numerical value type
17 Videos
- DIFFERENTIAL EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - SINGLE CORRECT ANSWER TYPES
74 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
- DIFFERENTIATIONBOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIATIONEXERCISE - Archives
14 Videos
Similar Questions
Spherical rain drop evaporates at a rate proportional to its surface area. The differential equation corresponding to the rate of change of the radius of the rain drop if the constant of proportionality is K>0 is (a) (b)(c)(d)(e)dyf((g)dt)(h)(i)+K=0(j) (k) (b) (l)(m)(n)(o)drp((q)dt)(r)(s)−K=0(t) (u) (c) (d)(e)(f)(g)drh((i)dt)(j)(k)=Kr(l) (m) (d) None of these
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
If an object of mass 2 kg and constant b=4N−sm has terminal speed vT in a liquid then time required to reach 0.63vT from start of the motion is :
View SolutionPath traced by a moving particle in space is called trajectory of the particle. Shape of trajectiry is decided by the forces acting on the particle. When a coordinate system is associated with a particle motion, the curve equation in which the particle moves [y=f(x)] is called equation of trajectory. It is just giving us the relation among x and y coordinates of the particle i.e. the locus of particle. To find equation of trajectory of a particle, find first x and y coordinates of the particle as a function of time eliminate the time factor.
In above the velocity (i.e.d→rdt) at t=0 is, if r =at i ^ −bt 2 j ^ :-
View SolutionA particle of mass 0.1kg is launched at an angle of 53∘ with the horizontal . The particle enters a fixed rough hollow tube whose length is slightly less than 12.5m and which is inclined at an angle of 37∘ with the horizontal as shown in figure. It is known that the velocity of ball when it enters the tube is parallel to the axis of the tube. The coefficient of friction betweent the particle and tube inside the tube is μ=38[ Take g=10m/g2]

The velocity of the particle as it enters the tube is :
View SolutionA particle of mass 0.1kg is launched at an angle of 53∘ with the horizontal . The particle enters a fixed rough hollow tube whose length is slightly less than 12.5m and which is inclined at an angle of 37∘ with the horizontal as shown in figure. It is known that the velocity of ball when it enters the tube is parallel to the axis of the tube. The coefficient of friction betweent the particle and tube inside the tube is μ=38[ Take g=10m/g2]

The kinetic energy of the particle when it comes out of the tube is approximately equal to :
View SolutionIf a particle with a=kv2 and initial velocity is u then velocity after S displacement. Here k is a constant
View SolutionAn object falling from rest in air is subject not only to the gravitational force but also to air resistance. Assume that the air resistance is proportional to the velocity with constant of proportionality as k>0 , and acts in a direction opposite to motion (g=9.8ms2). Then velocity cannot exceed. (a)9.8m/k m/s (b) 98/km m/s (c) k/g m/s (d) None of these
View SolutionConsider a spherical gaseous cloud of mass density ρ(r) in a free space where r is the radial distance from its centre. The gaseous cloud is made of particle of equal mass m moving in circular orbits about their common centre with the same kinetic energy K. The force acting on the particles is their mutual gravitational force. If ρ(r) is constant with time. the particle number density n(r)=ρ(r) /m is : (g =universal gravitational constant)
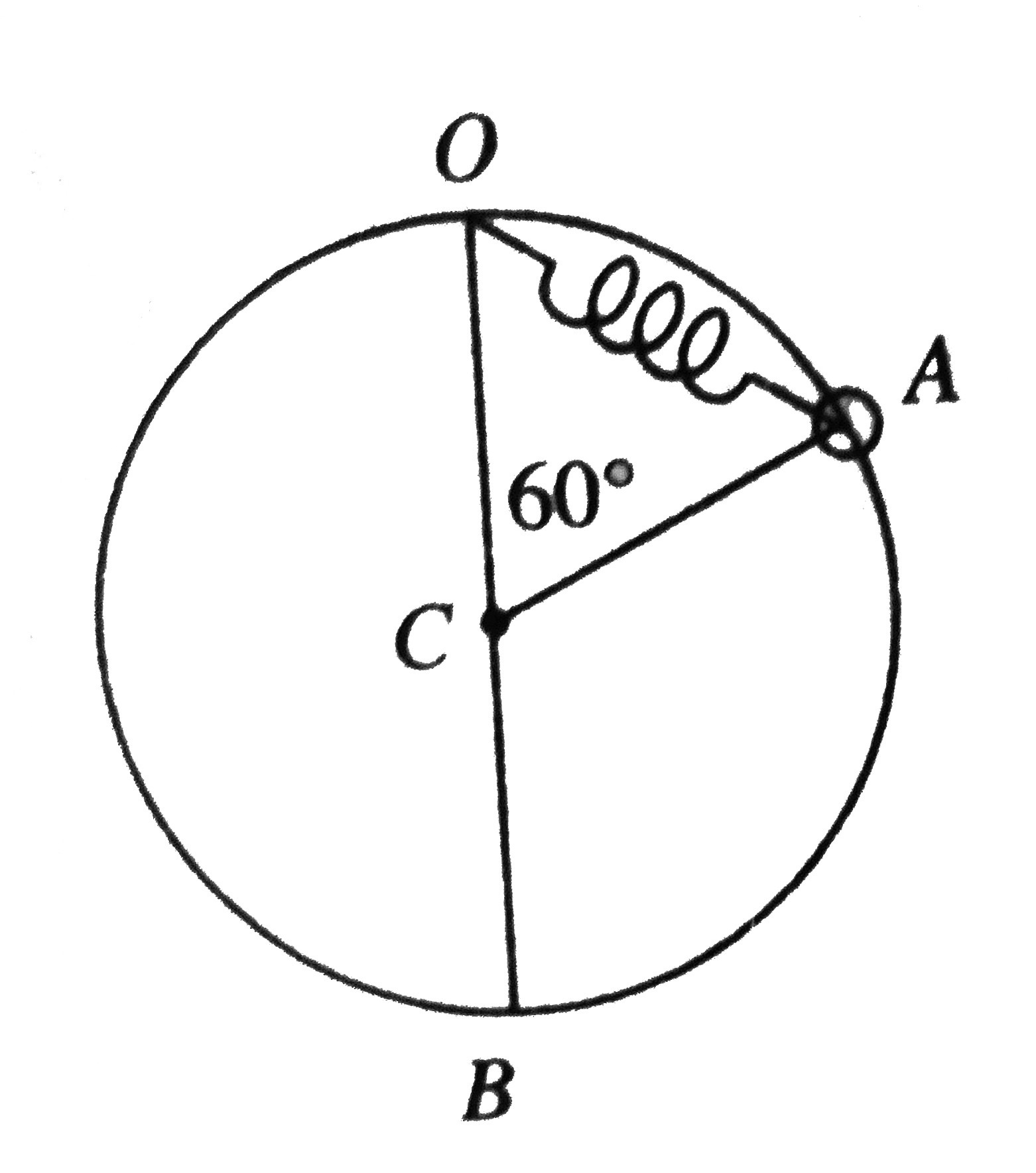
View SolutionA particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.
View SolutionIf velocity of particle is given by v=2t4, then its acceleration (dvdt) at any time t will be given by..
View Solution
