A particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.
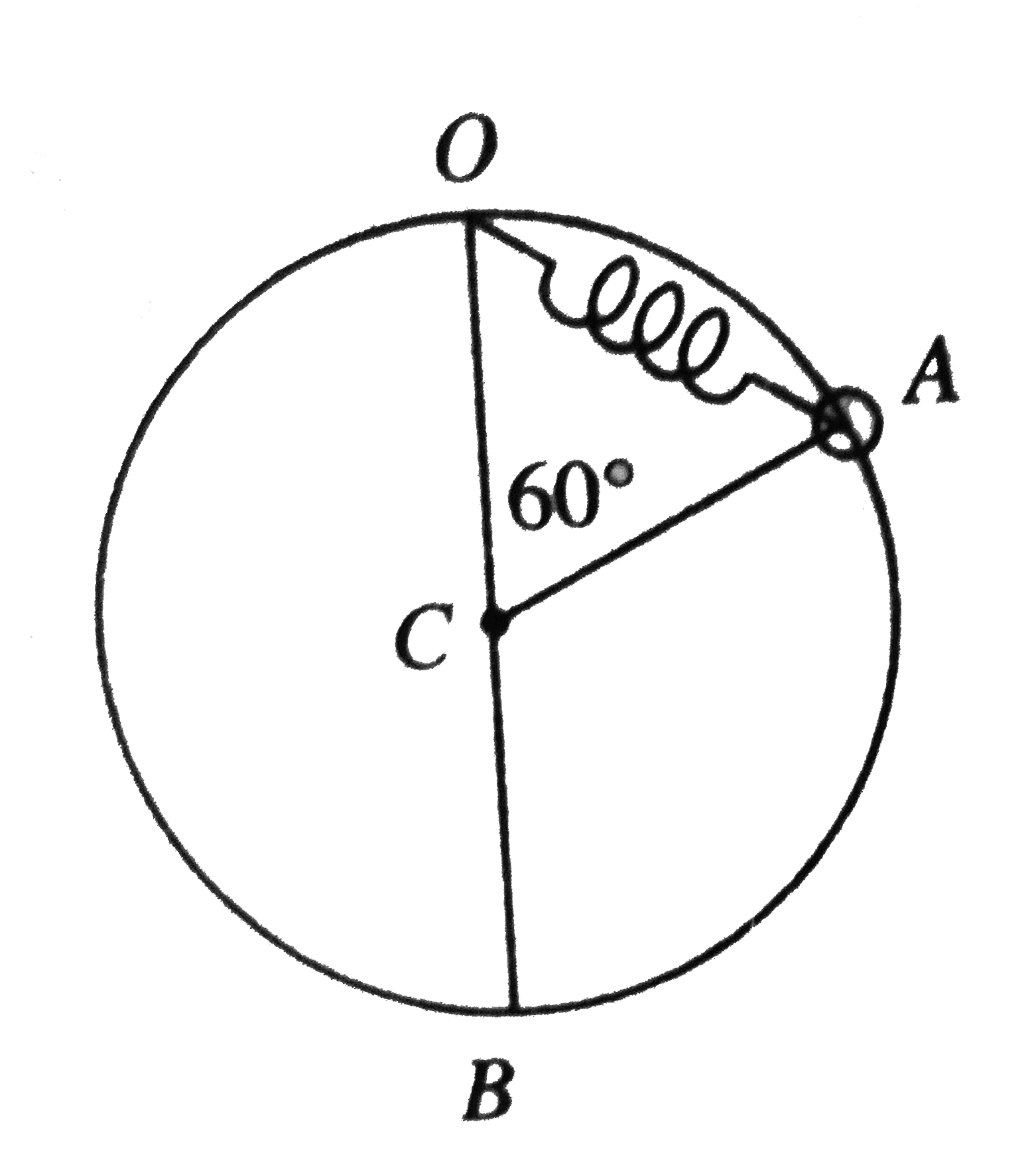

At position B, F.B.D. or ring
(since normal contact force is zero) ltbr Equation of motion kx−mg=mv2Br
x=OB− natural length of spring Z=2r−r
x=r
Kr−mg=mv2Br .(i)
From conservation of energy.
Total mechanical energy at A= total mechanical energy at B
gravitation PEA+ spring energy PEA)+K∈etice≠rgyKE_A<br>=GravitationPE_B+Spr∈ge≠rgyPE_B^()+ Kinetic energy KEB
mg(BC+CP)+12K(0)2+0
=0+12kx2+12mv2B
mg(r+rcos60∘)=12Kr2+12mv2B
⇒3mg2=12kr2+12mv2B
⇒3mg=kr2+mv2B
from (i) and (ii)
Kr2−mgr=3mg−kr2
⇒Kr2+4mgr⇒K=2mgr
⇒K=2510(0.2)⇒K=500Nm
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Single Correct Answer type491videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer5videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type22videos
COULOMB LAW AND ELECTRIC FIELD
Similar Questions
A particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u . The tension in the string T and acceleration of the particle is a at any position. Then T.a is zero at highest point if
View SolutionA particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u. The tension in the string is T and acceleration of the particle is a at any position then T. a' is positive at the lowest point for
View SolutionA particle is fastened at the end of a string and whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
View SolutionA particle of mass m is fixed to one end of a light rigid rod of length l and rotated in a vertical ciorcular path about its other end. The minimum speed of the particle at its highest point must be
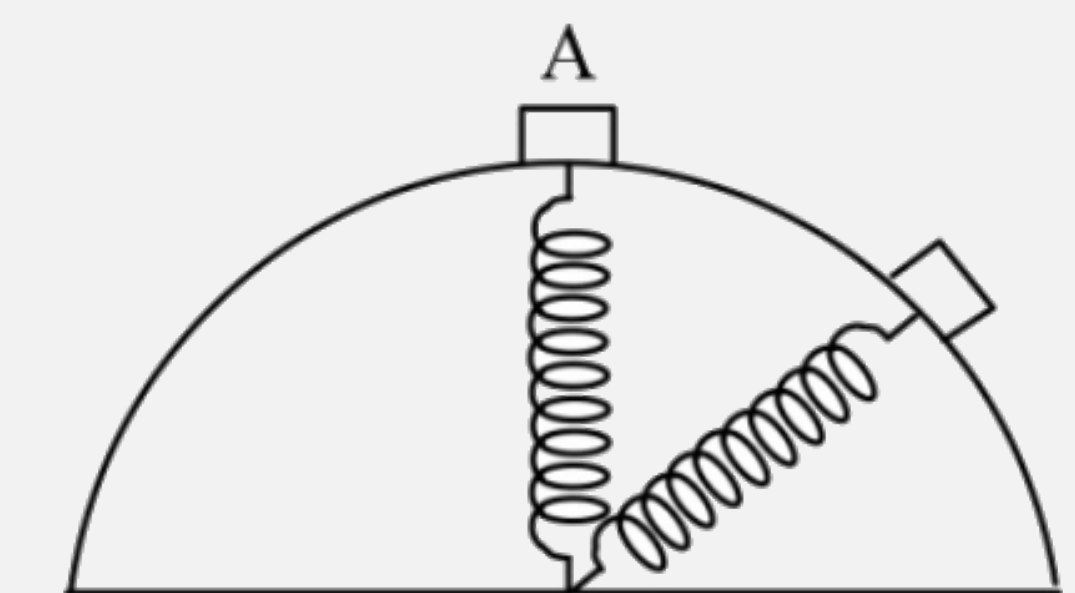
View SolutionA bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=3mgR is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60∘ with the vertical, then the natural length of the spring is
 View Solution
View SolutionA particle, held by a string whose other end is attached to a fixed point C, moves in a circle on a horizontal frictionless surface. If the string is cut, the angular momentum of the particle about the point C
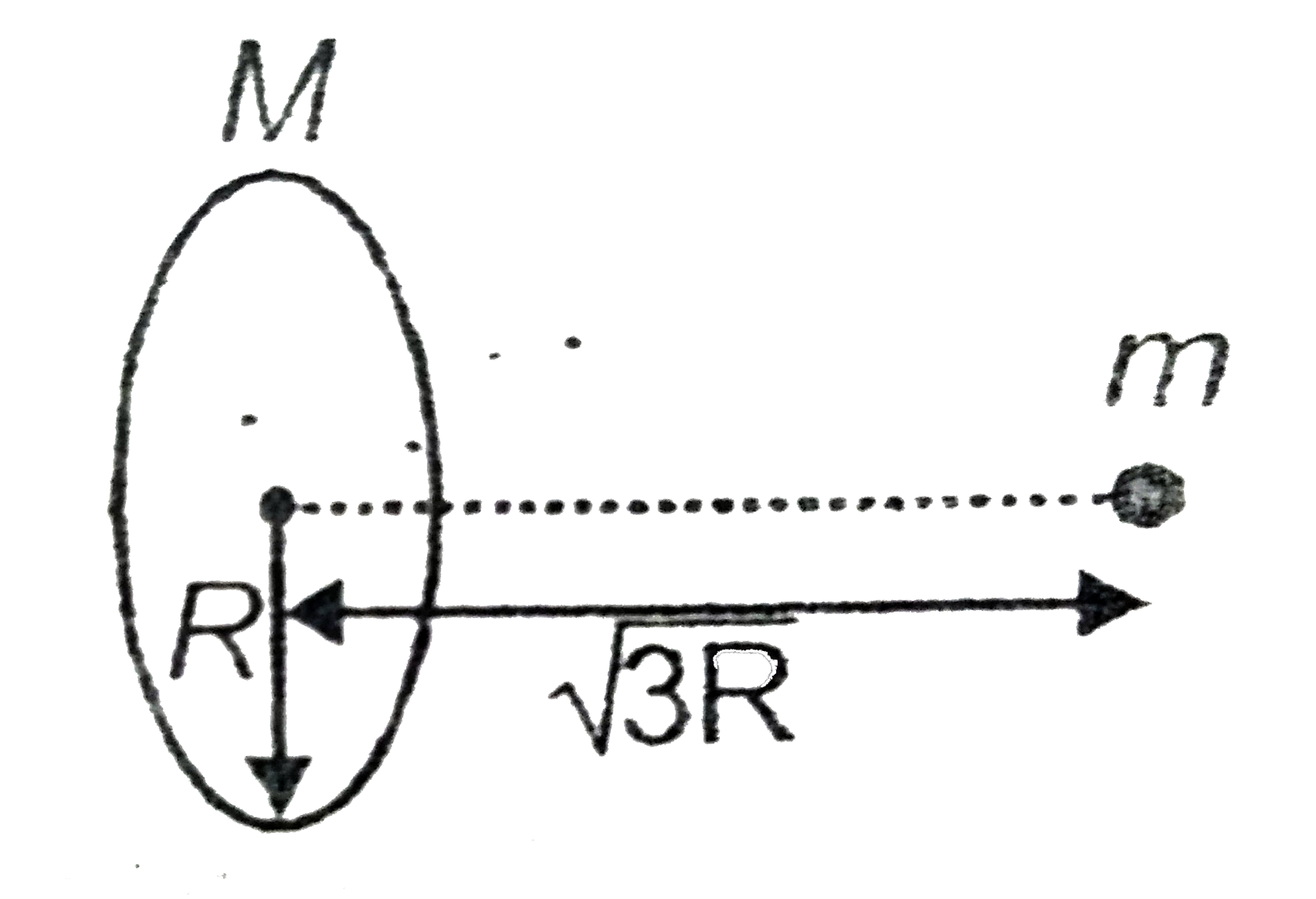
View SolutionA point particle of mass m is released from a distance √3R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.
 View Solution
View SolutionA ring mass m and radius R has three particle attached to the ring as shown in the figure. The centre of the centre v0. Find the kinetic energy of the system. (Slipping is absent).
 .View Solution
.View SolutionA particle of mass 200g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g=10ms2)
View SolutionA current carrying ring is placed in a horizontal plane. A charged particle is dropped along the axis of the ring to fall under the influence of gravity
View Solution

