A particle moves in a straight line and its speed depends on time as v=|2t−3| ∫vdt represent the distance travelled of the particle then find the displacement of the particle in 5s
Given that,
v=|2t−3|=⎧⎨⎩2t−3 t≥32−2t+3 t<32
S=∫50vdt=∫320vdt+∫532vdt
S=∫50vdt=∫320(−2t+3)dt+∫532(2t−3)dt
S=[−t2+3t]320+[t2−3t]532
S=−(32)2+3⋅(32)+25−15−(32)2+3⋅(32)
S=−2(94)+9+10
S=−92+19=292
S=292
(Answer)
Topper's Solved these Questions
Similar Questions
A particle moves in a straight line and its speed depends on time as v=|2t−3| ∫vdt representsthe distance travelled of the particle then find the displacement of the particle in 5 s
View SolutionA particle is moving in a straight line its speed depends on x as shown. The acceleration of particle is...
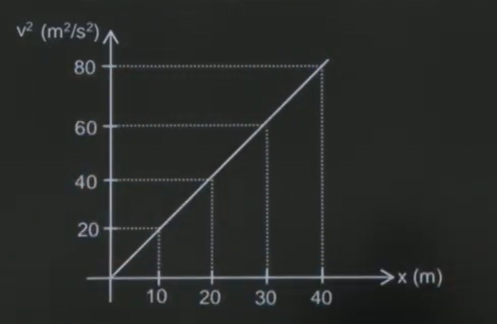 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
A particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
AAverage velcotu is 25/3ms−1BAverage speed is 10ms−1.CAverage velcotu is 5/3ms−1DAcceleration is 4ms−2 at t=o - Question 2 - Select One
Velocity time equation of a particle moving in a straight line is v=2t−4 for t≤2s and v=4−2t for t>2.The distance travelled by the particle in the time interval from t=0 to t=4s is (Here t is in second and v in m/s)
A12mB16mC4mD8m
A particle moves in a straight line obeying the relation x= t(t-1) where x= displacement in m and t= time in sec.Find the velocity of the particle when its displacement is zero.
View SolutionThe velocity-time graph of a particle moving in a staight line is shown in the . Find the displacement and the distance trav elled by the particle in 6s.
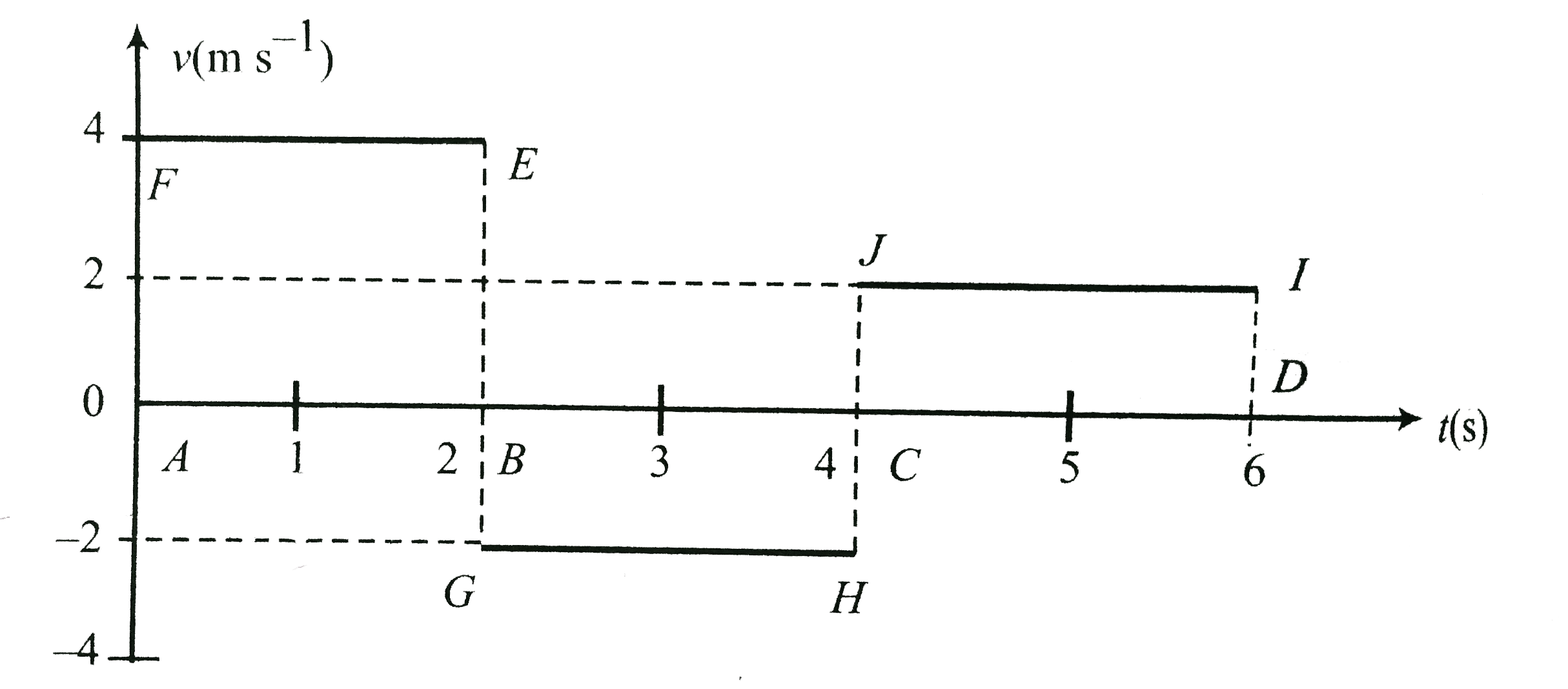 .View Solution
.View SolutionA particle is moving on a straight line and all the forces acting on it produce a constant power P calculate the distance travelled by the particle in the interval its speed increase from V to 2V.
View SolutionA particle moves in a straight line with constant speed of 4m/s for 2s, then with 6m/s for 3s. Find the average speed of the particle in the given time interval.
View SolutionA particle is moving in a straight line and its velocity varies with its displacement as v=√4+4s m/s. Assume s=0 at t=0. find the displacement of the particle in metres at t=1s.
View SolutionIf velocity is depend on time such that v = 4 – 2t. Find out distance travelled by particle from 1 to 3 sec
View Solution

