A particle is moving in a straight line and its velocity varies with its displacement as v=√4+4s m/s. Assume s=0 at t=0. find the displacement of the particle in metres at t=1s.
The correct Answer is:3
To solve the problem step by step, we will follow these instructions:
Step 1: Understand the relationship between velocity and displacement
The given relationship is:
v=√4+4s
Step 2: Square both sides to eliminate the square root
Squaring both sides gives:
v2=4+4s
Step 3: Rearrange the equation to express displacement in terms of velocity
Rearranging the equation, we get:
4s=v2−4
s=v2−44
Step 4: Use the relationship between velocity, acceleration, and time
Since velocity is a function of displacement, we can find acceleration. We know that:
v2=u2+2as
Here, we can compare this with our earlier equation.
Step 5: Identify initial conditions
At s=0 (initial displacement), we have:
v=√4+4(0)=√4=2m/s
Thus, the initial velocity u=2m/s.
Step 6: Find acceleration
From the equation v2=u2+2as:
- Initial velocity u=2m/s gives u2=4.
- From our rearranged equation, we can see that 4=4+4s implies a=2m/s2.
Step 7: Use the second equation of motion to find displacement at t=1s
Using the second equation of motion:
s=ut+12at2
Substituting u=2m/s, a=2m/s2, and t=1s:
s=2(1)+12(2)(12)
s=2+12(2)(1)
s=2+1=3m
Final Answer
The displacement of the particle at t=1s is 3m.
---
The given relationship is:
v=√4+4s
Squaring both sides gives:
v2=4+4s
Rearranging the equation, we get:
4s=v2−4
s=v2−44
Since velocity is a function of displacement, we can find acceleration. We know that:
v2=u2+2as
Here, we can compare this with our earlier equation.
At s=0 (initial displacement), we have:
v=√4+4(0)=√4=2m/s
Thus, the initial velocity u=2m/s.
From the equation v2=u2+2as:
- Initial velocity u=2m/s gives u2=4.
- From our rearranged equation, we can see that 4=4+4s implies a=2m/s2.
Using the second equation of motion:
s=ut+12at2
Substituting u=2m/s, a=2m/s2, and t=1s:
s=2(1)+12(2)(12)
s=2+12(2)(1)
s=2+1=3m
The displacement of the particle at t=1s is 3m.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE (MATRIX MATCH TYPE QUESTIONS )
1 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)
12 Videos
Similar Questions
Velocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
View SolutionA particle is moving in a straight line along X-axis and its x-coordinate varies with time as:
x=t2−4t+6
Find the distance and displacement of particle in time interval t=0to t=3s.
View Solution
Knowledge Check
For a particle moving along a straight line, its velocity 'v' and displacement 's' are related as v2=cs, here c is a constant. If the displacement of the particle at t=0 is zero, its velocity after 2 sec is:
Ac2s0Bcs0Cc2s−1Dcs−1A particle moving in a straight in a straight line has velocity and displacement equation as
v=4√1+s,
where v is in m/s and s is in m. The initial velocity of the particle is:A4 m/sB16 m/sC2 m/sDzeroIf the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
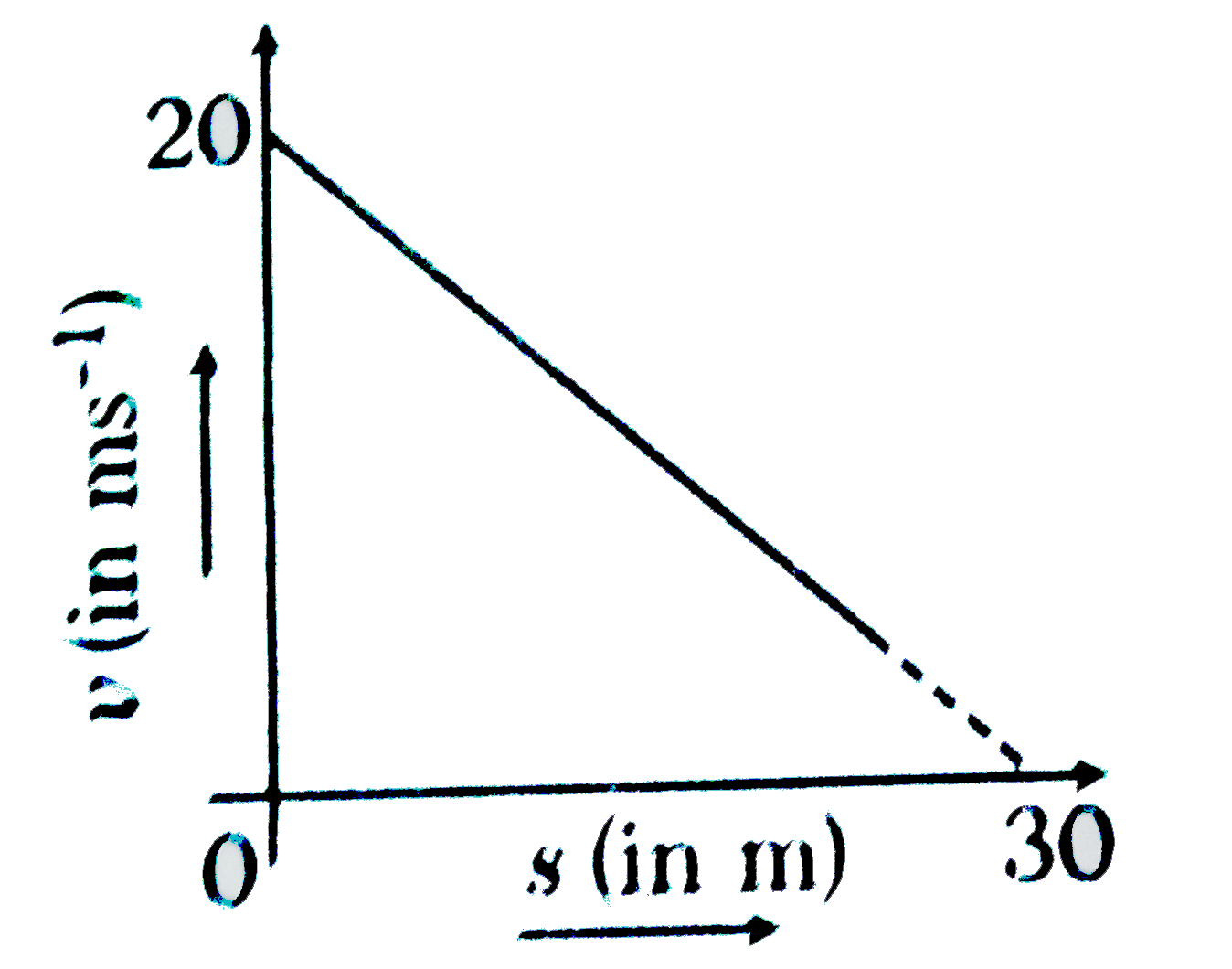 A23ms−2B−23ms−2C203ms−2D−203ms−2
A23ms−2B−23ms−2C203ms−2D−203ms−2
Velocity of a particle moving in a straight line varies with its displacement as v=√4+4xm/s where x is displacement. Displacement of particle at time t = 0 is x = 0. Find displacement (in m) of particle in 2 sec.
View SolutionIf the velocity v of a particle moving along a straight line decreases linearly with its displacement from 20m/s to a value approaching zero at s=30m, determine the acceleration of the particle when s=15m.
View SolutionA particle moves in a straight line and its speed depends on time as v=|2t−3| ∫vdt representsthe distance travelled of the particle then find the displacement of the particle in 5 s
View SolutionA particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
View SolutionA particle is moving in a straight line under constant acceleration of 4m/s2. If its velocity at t=0 is 10 m//s, the displacement of particle in the 5th second of its motion is
View Solution
