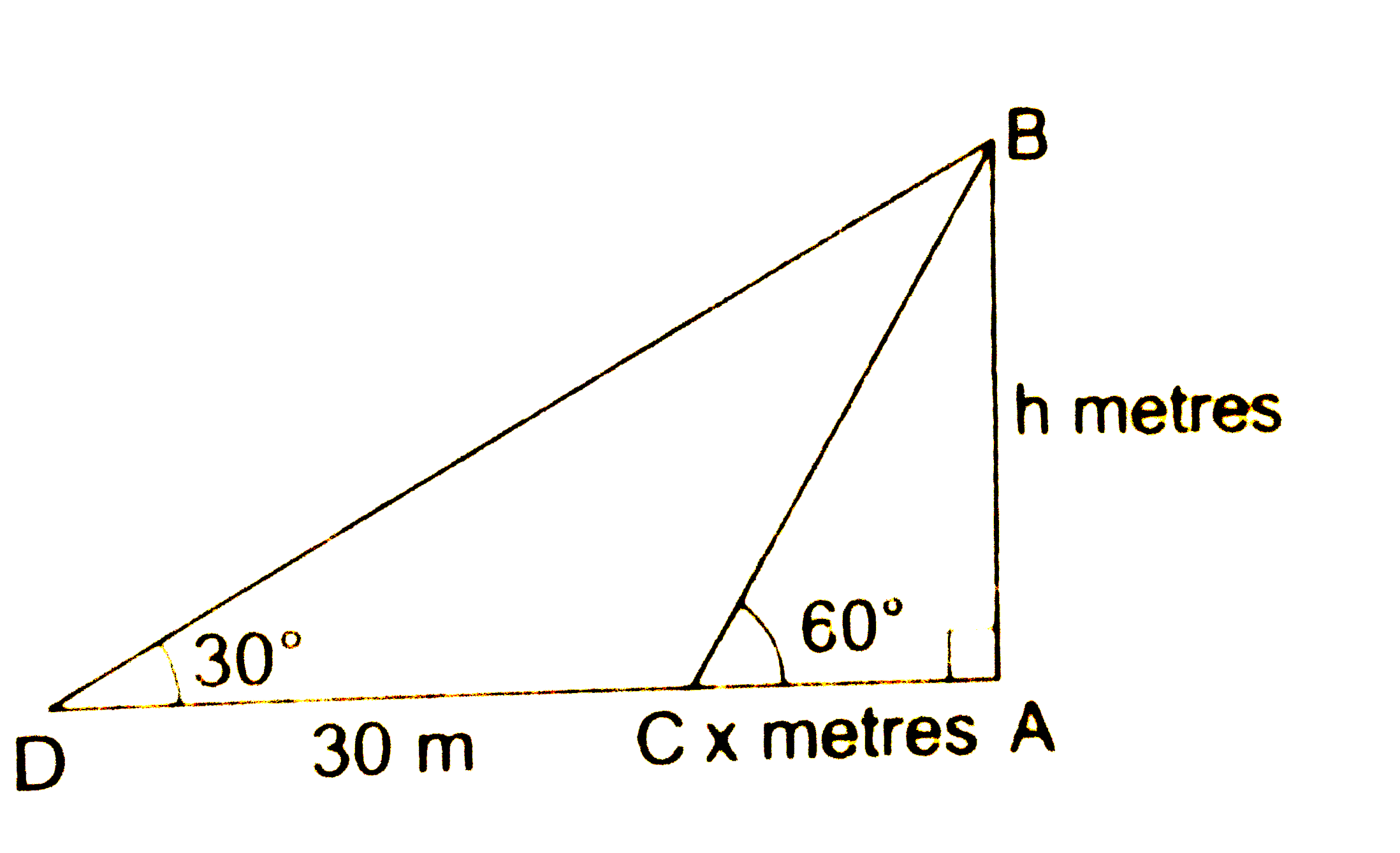
A person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is $60^{0} .$ When he moves 40 metres away from the bank, he finds the angle of elevation to be $30^{\circ} .$ Find the height of the tree and the width of the river.

Video Solution

Text Solution

Verified by Experts

Let AB be the tree and AC of the river.
Let C and D be the two positions of the person.
Then, $∠ A C B = 60^{\circ}, ∠ A D B = 30^{\circ}, ∠ D A B = 90^{\circ}$ and $C D = 30 m$ .
Let AB = h metres and AC = x metres.
From right $Δ C A B$ we have
$\frac{A C}{A B} = {cot 60}^{\circ} = \frac{1}{\sqrt{3}}$
$\Rightarrow \frac{x}{h} = \frac{1}{\sqrt{3}} \Rightarrow x = \frac{h}{\sqrt{3}} ....... (i)$
$\Rightarrow \frac{x + 30}{h} = \sqrt{3} \Rightarrow x = \sqrt{3} h - 30$ .
Equating the value of x from (i) and (ii) we get
$\frac{h}{\sqrt{3}} = \sqrt{3} h - 30 \Rightarrow h = 3 h - 30 \sqrt{3}$
$\Rightarrow 2 h = 30 \sqrt{3} \Rightarrow h = 15 \sqrt{3} = 15 \times 1.732 = 25.98$ .
Putting $h = 15 \sqrt{3}$ in (i), we get $x = \frac{15 \sqrt{3}}{\sqrt{3}} = 15$ .
Hence, the height of the treeis $25.98$ m and the width of the river is $15$ metres.

Updated on:21/07/2023

A person standing on the bank of a river observes that the angle subtended by a tree on the opposite of bank is $60^{\circ}$ . When he retires 40 m.from the bank, he finds the angle to be $30^{\circ}$ . What is the breadth of the river ?
A20 m
B24 m
C40 m
D64 m
A person standing on the bank of a river observes that the angle subtended by a tree on the opposite of bank is $60^{\circ}$ . when he returns 40 m from the bank, he finds the angle to be $30^{\circ} .$ What is the breadth of the river?
A40 m
B60 m
C20 m
D30 m
A person standing on the bank of a river finds that the angle of elevation of the top of a tower on the opposite bank is $45^{\circ}$ , then which of the following statements is correct ?
ABreadth of the river is twice the height of the tower
BBreadth of the river and the height of the tower are the same
CBreadth of the river is half of the height of the tower
Dnone of these