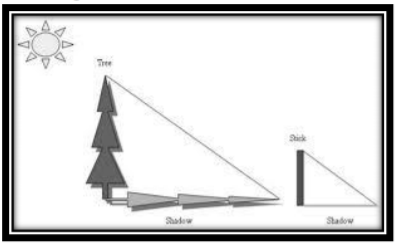
The shadow of a 5-m-long stick is 2m long. At the same time, the length of the shadow of a 12.5m high tree is
3m
3.5m
4.5m
5m
The correct Answer is:D
To solve the problem, we will use the concept of similar triangles, which states that the ratios of the lengths of objects to their shadows will be equal when measured at the same time.
1. Identify the lengths and shadows:
- Length of the stick (L1) = 5 m
- Length of the shadow of the stick (S1) = 2 m
- Length of the tree (L2) = 12.5 m
- Length of the shadow of the tree (S2) = ?
2. Set up the proportion:
Since the stick and the tree cast shadows at the same time, we can set up the following proportion based on the similarity of triangles:
L1S1=L2S2
3. Substitute the known values into the proportion:
52=12.5S2
4. Cross-multiply to solve for S2:
5⋅S2=12.5⋅2
5. Calculate the right-hand side:
5⋅S2=25
6. Divide both sides by 5 to isolate S2:
S2=255=5 m
Final Answer:
The length of the shadow of the 12.5 m high tree is 5 m.
- Length of the stick (L1) = 5 m
- Length of the shadow of the stick (S1) = 2 m
- Length of the tree (L2) = 12.5 m
- Length of the shadow of the tree (S2) = ?
Since the stick and the tree cast shadows at the same time, we can set up the following proportion based on the similarity of triangles:
L1S1=L2S2
52=12.5S2
5⋅S2=12.5⋅2
5⋅S2=25
S2=255=5 m
The length of the shadow of the 12.5 m high tree is 5 m.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Exercise 1438videos
HEIGHTS AND DISTANCES
- BOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)34videos
COORDINATE GEOMETRY
- BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - QUESTION2videos
LINEAR EQUATIONS IN TWO VARIABLES
Similar Questions
Knowledge Check
- Question 1 - Select One
A vertical stick 1.8 m long casts a shadow 45 cm long on the ground. At the same time, what is the length or the shadow of a pole 6 m high?
A2.4mB1.35mC1.5mD13.5m
A 5 m 60 cm high vertical pole casts a shadow 3 m 20 cm long. Find at the same time(i) the length of the shadow cast by another pole 10 m 50 cm high (ii) the height of a pole which casts a shadow 5m long.
View SolutionA vertical pole 5 m 60 cm high casts a shadow 3 m 20 cm long. Find at the same time (i) the length of shadown cast by another pole 10 m 50 cm high.
(ii) the height of a pole which casts a shadow 5 m long.View SolutionThe shadow of a pole 6 metre high is 15 metre long and at the same time the shadow of a tree is 25 metre long. What is the height of the tree ?
View SolutionFind the height of a pole if the length of its shadow is 20 metres if at the same time the length of shadow of a 1 metre stick is 55 cm
View SolutionA water tank casts a shadow 21 m long. A tree of height 9.5 m casts a shadow 8 m long at the same time. The lengths of the shadows are directly proprotional to their heights. Find the height of the tank.
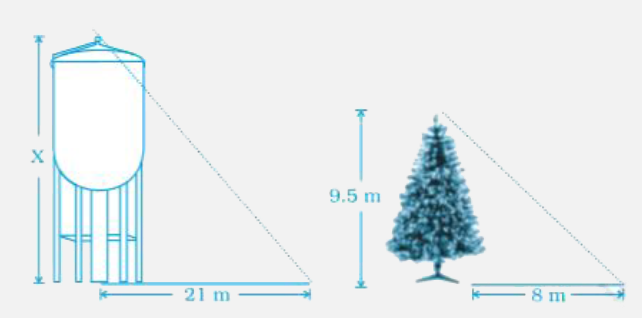 View Solution
View SolutionA vertical pole of length 8 m casts a shadow of 15 m long on the ground. At the same time, a tower casts a shadow 45 m long. Find the height of the tower.
View Solution
Vijay is trying to find the average height of a tower near his house. He is using the properties of similar triangles.The height of Vijay’s house if 20m when Vijay’s house casts a shadow 10m long on the ground. At the same time, the tower casts a shadow 50m long on the ground and the house of Ajay casts 20m shadow on the ground.
What will be the length of the shadow of the tower when Vijay’s house casts a shadow of 12m?View Solution


 (i)3m
(i)3m