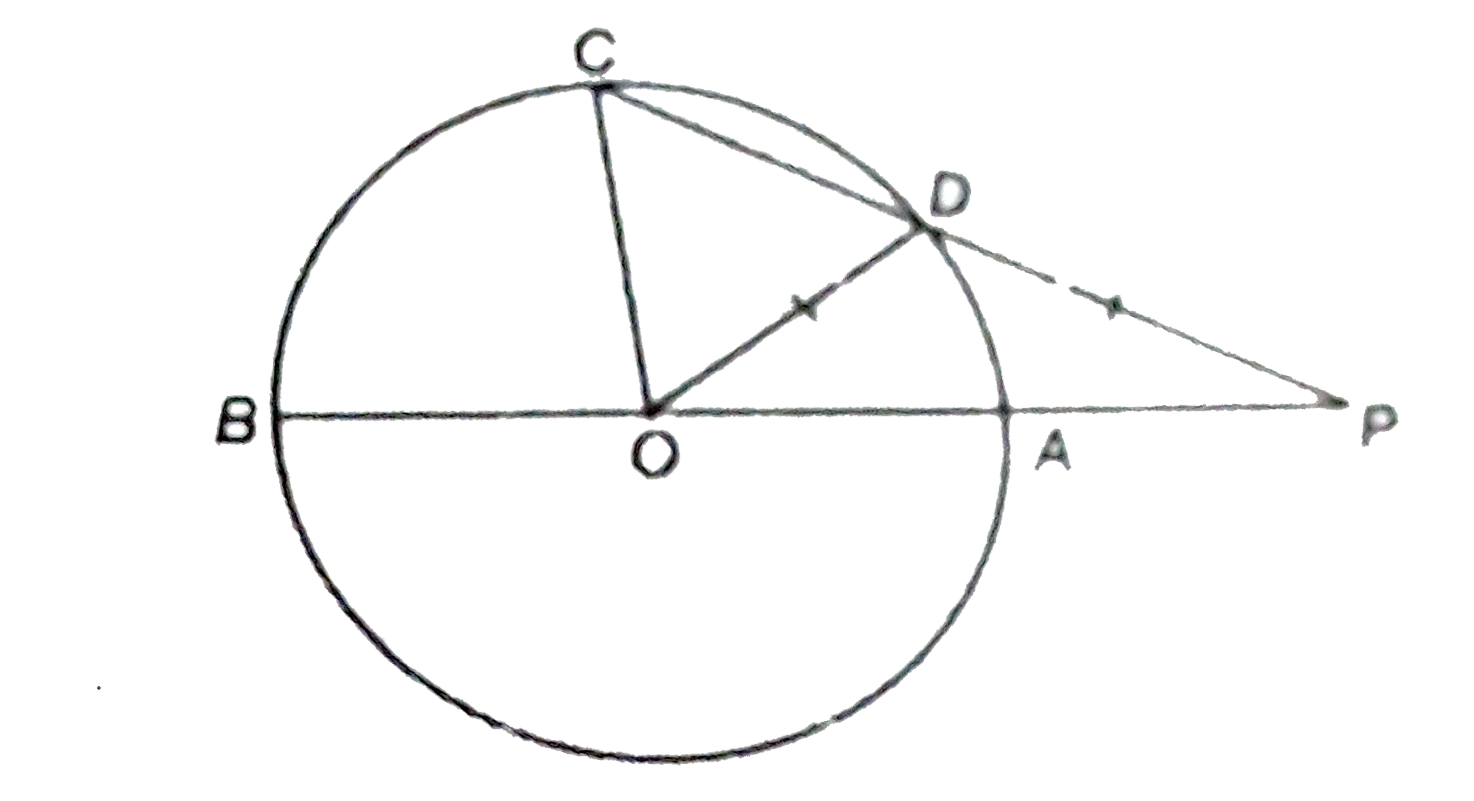
A point P lies outside the circle with centre O. two lines PAOB and PDC are drawn on the circle from P. if PD =OD, then prove that arc BC=3×ArcAD.
In ΔDOP,
DO=DP
⇒∠DPO=∠DOP
Let ∠DPO=∠DOP=x
Now in ΔODP,
∠ODC is the exterior angle
∴∠ODC=∠DOP+∠DPO
x+x
2x
In ΔOCD,
OC=OD
⇒∠ODC=∠OCD=2x
∴∠COD=180∘−∠ODC−∠OCD
180∘−2x−2x
180∘−4x
Now, ∠BOC+∠COD+∠DOP=180∘ (L.P.A)
⇒∠BOC+180∘−4x+x=180∘
⇒∠BOC=3x
∴∠BOC∠DOP=3xx
⇒∠BOC∠DOA=3
⇒ArcBCArcAD=3 (length of arcs are proportional to their corresponding angles )
⇒ArcBC=3×ArcAD
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
From a point P outside a circle with centre O, tangents PA and PB are drawn to the circle. Prove that OP is the right bisector of the line segment AB.
View SolutionIf from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC=120∘, prove that BC+BD=BO.
View Solution
Knowledge Check
From a point P outside the circle with centre O, two tangents PA and PB are drawn to meet the circle at A and B respectively. If ∠APB=70∘, then ∠OAB is equal to :
केंद्र O वाले वृत्त के बाहर स्थित किसी बिंदु P से दो स्पर्श रेखाएं PA और PB खींची जाती हैं जो वृत्त से क्रमशः A और B मिलती हैं | यदि ∠APB=70∘ है, तो कोण OAB का मान ज्ञात करें |A35∘B65∘C45∘D55∘P is a point outside a circle with centre O, and it is 14 cm away from the centre. A secant PAB drawn from P intersects the circle at the points A and B such that PA = 10 cm and PB = 16 cm. The diameter of the Circle is:
A10 cmB13 cmC12 cmD11 cmPA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If ∠PAB=47∘ , then ∠OAB is equal to :
A43∘B53∘C50∘D20∘
In the figure, two circles with centers O and P intersect each other at points D and C. Line AB intersects the circle with centre O at points A and B and touches the circle with centre P at point E. Prove ∠ADE+∠BCE=180∘.

View Solution
A point P is 13 cm from the centre of the circle. The two tangent PQ and PR are drawn from the point P, The length of the tangent drawn from P to the circle is 12 cm.
Find the radius of the circle.
View Solution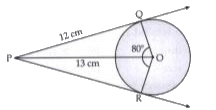
A point P is 13 cm from the centre of the circle. The two tangent PQ and PR are drawn from the point P, The length of the tangent drawn from P to the circle is 12 cm.
∠PQO is equal to ………. .
View Solution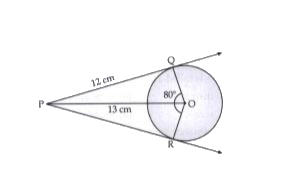
A point P is 13 cm from the centre of the circle. The two tangent PQ and PR are drawn from the point P, The length of the tangent drawn from P to the circle is 12 cm.
Find the length of OR.
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=40∘, then ∠OABis equal to:
View Solution
