From a point $P$ outside a circle with centre $O$ , tangents $P A$ and $P B$ are drawn to the circle. Prove that $O P$ is the right bisector of the line segment $A B$ .

Video Solution

Text Solution

Verified by Experts

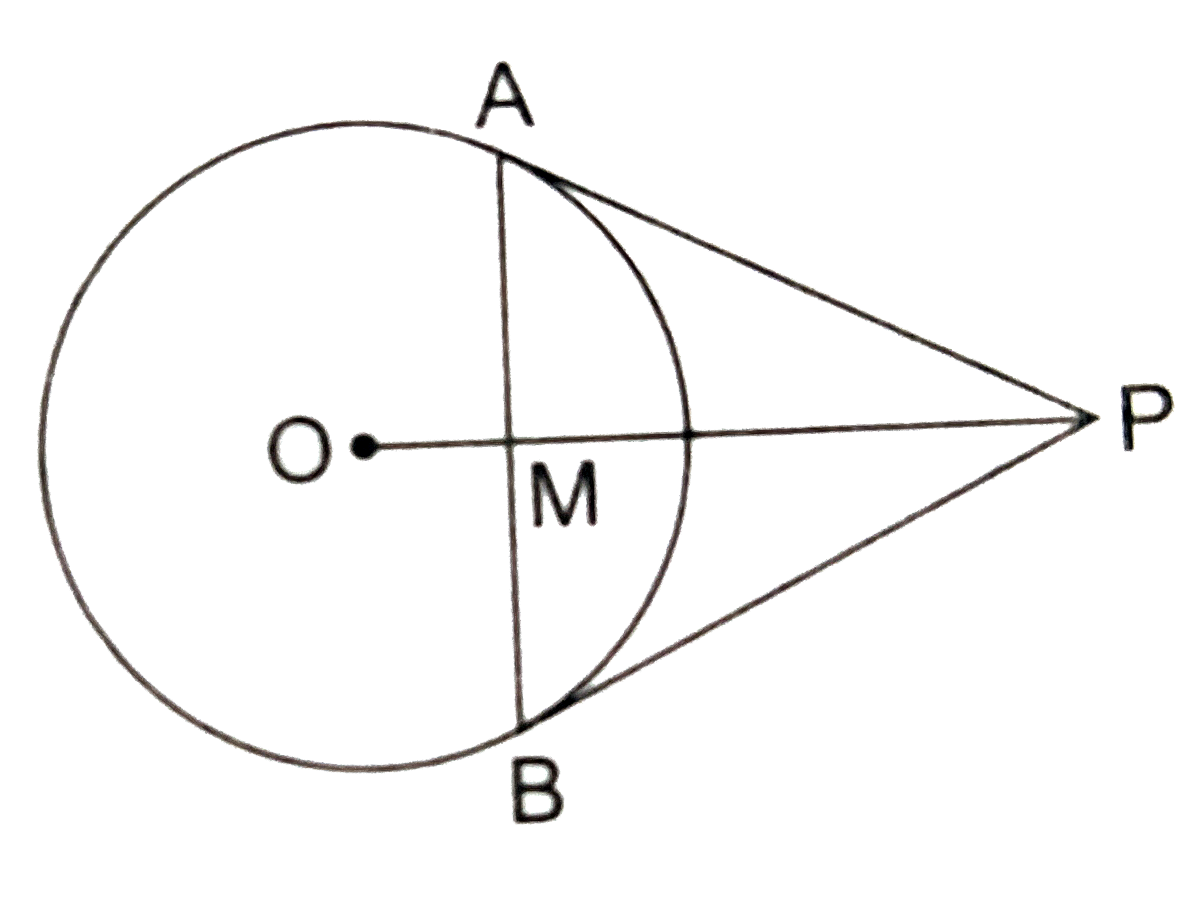
GIVEN $P A$ and $P B$ are tangents to a circle with centre $O$ from an external point $P$ .
TO PROVE $O P$ is the right bisector of $A B$ .
CONSTRUCTION Join $A B$ . Let $A B$ intersect $O P$ at $M$ .
PROOF In $Δ M A P$ and $Δ M B P$ , we have
$P A = P B$ [ $∵$ tangents to a circle from an external point are equal]
$M P = M P$ [common]
$∠ M P A = ∠ M P B$ [ $∵$ tangents from an external point are equally inclined to the line segment joining the centre to that point i.e., $∠ O P A = ∠ O P B$ ]
$∴ M A P ≅ Δ M B P$ [by SAS-congruence]
And so, $M A = M B$ [cpct]
and $∠ A M P = ∠ B M P$ [cpct]
But $∠ A M P + ∠ B M P = 180^{\circ}$ [linear pair]
$∴ ∠ A M P = ∠ B M P = 90^{\circ}$
Hence, $O P$ is the right bisector of $A B$ .

|

Updated on:21/07/2023

Class 10 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
From a point P outside the circle with centre O, two tangents PA and PB are drawn to meet the circle at A and B respectively. If $∠ A P B = 70^{\circ}$ , then $∠ O A B$ is equal to :
केंद्र O वाले वृत्त के बाहर स्थित किसी बिंदु P से दो स्पर्श रेखाएं PA और PB खींची जाती हैं जो वृत्त से क्रमशः A और B मिलती हैं | यदि $∠ A P B = 70^{\circ}$ है, तो कोण OAB का मान ज्ञात करें |
A $35^{\circ}$
B $65^{\circ}$
C $45^{\circ}$
D $55^{\circ}$
Question 2 - Select One
From a point P, two tangents PA and PB are drawn to a circle with centre O. If OP is equal to diameter of the circle, then $∠ A P B$ is
A $45^{\circ}$
B $90^{\circ}$
C $30^{\circ}$
D $60^{\circ}$
Question 3 - Select One
From a point P two tangents PA and PB are drawn to a circle with centre O.if OP is equal to diameter of the circle then $∠ A P B$ is
A $60^{\circ}$
B $45^{\circ}$
C $90^{\circ}$
D $30^{\circ}$

RS AGGARWAL-CIRCLES-Test Yourself

Home
Ask Doubt
Profile