A random variable has the following probability distribution:
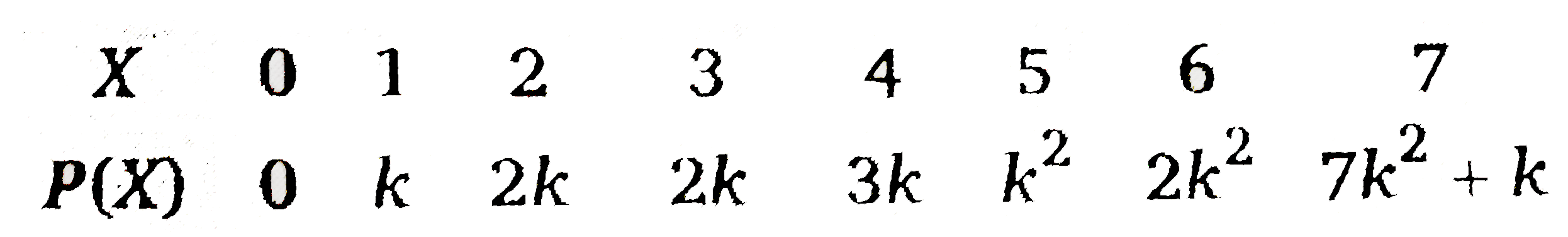
Determine :
(i)
(ii)
(iii)
(iv)
The correct Answer is:N/a
(i) Since the sum of the probabilities of a probability distribution of a random variable is 1.
i.e.
Therefore
or
or
Because is not possible as the probability of an event can never be negative.
(ii)
(iii)
(iv)
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABIILITYEXERCISE - Exercise 13.515videos
PROBABIILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABIILITYEXERCISE - Miscellaneous Exercise19videos
PROBABIILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABIILITYEXERCISE - Exercise 13.314videos
PROBABIILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice15videos
MATRICES
- BOOK - NAGEEN PRAKASHANCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Miscellaneous Exercise19videos
RELATIONS AND FUNCTIONS
Similar Questions
A random variable X has the following probability distribution find K.
 View Solution
View SolutionA random variable X has the follwing probability distribution:

Find k.View SolutionA random variable X has the following probability distribution:
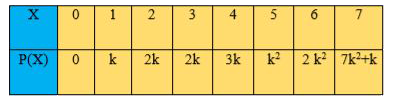
Determine : (i) k (ii) P(X<3) (iii) P(X>4)View SolutionA random variable X has the following probability distribution:Determine (i) k (ii) P(X<3)(iii) P(X>6) (iv) P(0<X<3)
View SolutionA random variable X has the following probability distribution :

Determine
(i) k (ii) P(X<3)
(iii) P(X>6) (iv) P(0<X<3).View SolutionA random variable X has the following probability distribution:

Then E(X) = …….View SolutionA random variable X has the following probability distribution:

then Var(X)=____View SolutionA random variable X has the follwing probability distribution:

Find P(0<X<4)View SolutionA random variable X has the following probability distribution.
Then, the mean of X is
 View Solution
View SolutionA random variable X has the following probability distribution:

Determine (i)k,(ii)P(X<3),(iii)P(0<X<3),(iv)P(X>4).View Solution

