A random variable X has the following probability distribution:Determine (i) k (ii) P(X<3)(iii) P(X>6) (iv) P(0<X<3)
To solve the problem step by step, we will follow the instructions given in the video transcript and break down each part of the question.
Given Probability Distribution
Let the random variable X take values from 0 to 7 with the following probabilities:
- P(X=0)=k
- P(X=1)=2k
- P(X=2)=2k
- P(X=3)=3k
- P(X=4)=k2
- P(X=5)=2k2
- P(X=6)=7k2
- P(X=7)=k
Step 1: Determine k
The sum of all probabilities must equal 1:
P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5)+P(X=6)+P(X=7)=1
Substituting the probabilities:
k+2k+2k+3k+k2+2k2+7k2+k=1
Combining like terms:
(3k+2k+2k+3k+k+7k2+k2)=1
This simplifies to:
8k+10k2=1
Rearranging gives:
10k2+8k−1=0
Now we can use the quadratic formula k=−b±√b2−4ac2a where a=10,b=8,c=−1:
k=−8±√82−4⋅10⋅(−1)2⋅10
Calculating the discriminant:
k=−8±√64+4020=−8±√10420=−8±2√2620=−4±√2610
Calculating the two possible values:
1. k=−4+√2610
2. k=−4−√2610 (not valid since k must be non-negative)
Calculating k:
Using a calculator, √26≈5.099:
k≈−4+5.09910≈1.09910≈0.1099≈110
Thus, k=110.
Step 2: Calculate P(X<3)
To find P(X<3), we need to sum the probabilities for X=0,1,2:
P(X<3)=P(X=0)+P(X=1)+P(X=2)=k+2k+2k=5k
Substituting k=110:
P(X<3)=5⋅110=510=12
Step 3: Calculate P(X>6)
To find P(X>6), we only consider X=7:
P(X>6)=P(X=7)=k=110
Step 4: Calculate P(0<X<3)
To find P(0<X<3), we consider X=1,2:
P(0<X<3)=P(X=1)+P(X=2)=2k+2k=4k
Substituting k=110:
P(0<X<3)=4⋅110=410=25
Summary of Answers
(i) k=110
(ii) P(X<3)=12
(iii) P(X>6)=110
(iv) P(0<X<3)=25
Let the random variable X take values from 0 to 7 with the following probabilities:
- P(X=0)=k
- P(X=1)=2k
- P(X=2)=2k
- P(X=3)=3k
- P(X=4)=k2
- P(X=5)=2k2
- P(X=6)=7k2
- P(X=7)=k
The sum of all probabilities must equal 1:
P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5)+P(X=6)+P(X=7)=1
Substituting the probabilities:
k+2k+2k+3k+k2+2k2+7k2+k=1
Combining like terms:
(3k+2k+2k+3k+k+7k2+k2)=1
This simplifies to:
8k+10k2=1
Rearranging gives:
10k2+8k−1=0
Now we can use the quadratic formula k=−b±√b2−4ac2a where a=10,b=8,c=−1:
k=−8±√82−4⋅10⋅(−1)2⋅10
Calculating the discriminant:
k=−8±√64+4020=−8±√10420=−8±2√2620=−4±√2610
Calculating the two possible values:
1. k=−4+√2610
2. k=−4−√2610 (not valid since k must be non-negative)
Using a calculator, √26≈5.099:
k≈−4+5.09910≈1.09910≈0.1099≈110
Thus, k=110.
To find P(X<3), we need to sum the probabilities for X=0,1,2:
P(X<3)=P(X=0)+P(X=1)+P(X=2)=k+2k+2k=5k
Substituting k=110:
P(X<3)=5⋅110=510=12
To find P(X>6), we only consider X=7:
P(X>6)=P(X=7)=k=110
To find P(0<X<3), we consider X=1,2:
P(0<X<3)=P(X=1)+P(X=2)=2k+2k=4k
Substituting k=110:
P(0<X<3)=4⋅110=410=25
(i) k=110
(ii) P(X<3)=12
(iii) P(X>6)=110
(iv) P(0<X<3)=25
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - Solved Examples36videos
PROBABILITY
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - EXERCISE 13.117videos
PROBABILITY
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - EXERCISE 13.218videos
PROBABILITY
- BOOK - NCERTCHAPTER - MATRICESEXERCISE - EXERCISE 3.312videos
MATRICES
- BOOK - NCERTCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 1.314videos
RELATIONS AND FUNCTIONS
Similar Questions
A random variable X has the following probability distribution:Determine (i) k (ii) P(X<3)(iii) P(X>6) (iv) P(0<X<3)
View SolutionA random variable X has the following probability distribution :

Determine
(i) k (ii) P(X<3)
(iii) P(X>6) (iv) P(0<X<3).View SolutionA random variable X has the following probability distribution:
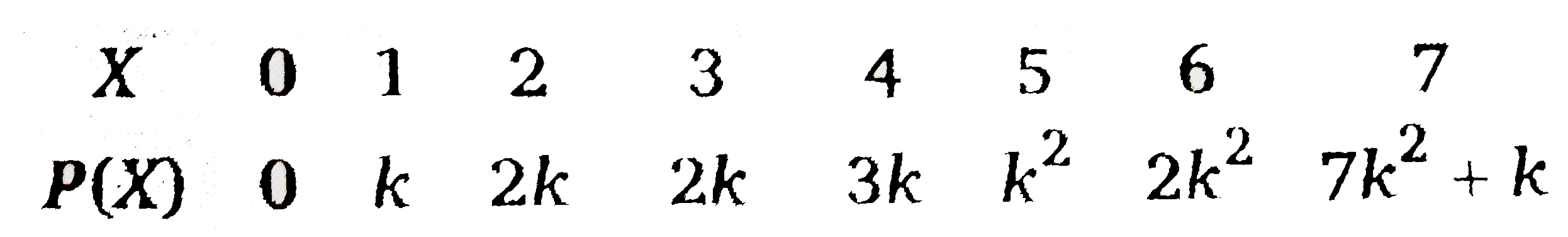
Determine :
(i) k
(ii) P(X<3)
(iii) P(X>6)
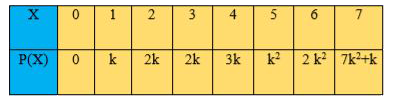
(iv) P(0<X<3)View SolutionA random variable X has the following probability distribution:

Determine (i)k,(ii)P(X<3),(iii)P(0<X<3),(iv)P(X>4).View SolutionA random variable X has the following probability distribution:
Determine : (i) k (ii) P(X<3) (iii) P(X>4)View SolutionA random variable X has the following probability distribution find K.
 View Solution
View SolutionA random variable X has the follwing probability distribution:

Find k.View SolutionA random variable X has the following probability distribution:

Then E(X) = …….View SolutionA random variable X has the following probability distribution:

then Var(X)=____View SolutionA random variable X has the following probability distribution.
Then, the mean of X is
 View Solution
View Solution

