A real number x is selected at random from the solution set of inequation y2−y−6≤0. What is the probability that (x+1)(x−2)x−4≥0?
To solve the problem step by step, we need to follow these steps:
Step 1: Solve the Inequation y2−y−6≤0
1. Factor the quadratic expression:
y2−y−6=(y−3)(y+2)≤0
2. Find the roots:
The roots of the equation are y=3 and y=−2.
3. Test intervals:
We will test the sign of the expression in the intervals defined by the roots:
- For y<−2: Choose y=−3 → (−)(−)>0
- For −2<y<3: Choose y=0 → (−)(+)<0
- For y>3: Choose y=4 → (+)(+)>0
4. Determine the solution set:
The solution set where the expression is less than or equal to zero is:
y∈(−2,3)
Step 2: Find the Probability that (x+1)(x−2)x−4≥0
1. Set up the inequality:
We need to solve:
(x+1)(x−2)x−4≥0
2. Identify the critical points:
The critical points are found by setting the numerator and denominator to zero:
- x+1=0 → x=−1
- x−2=0 → x=2
- x−4=0 → x=4
3. Test intervals:
We will test the sign of the expression in the intervals defined by the critical points:
- For x<−1: Choose x=−2 → (+)(−)/(−)>0
- For −1<x<2: Choose x=0 → (+)(−)/(+)<0
- For 2<x<4: Choose x=3 → (+)(+)/(+)>0
- For x>4: Choose x=5 → (+)(+)/(+)>0
4. Determine the solution set:
The solution set where the expression is greater than or equal to zero is:
x∈(−∞,−1)∪(2,4)∪(4,∞)
Step 3: Find the Intersection of the Two Solution Sets
1. Identify the total solution set:
From Step 1, we have:
x∈(−2,3)
2. Identify the favorable solution set:
From Step 2, we have:
x∈(−∞,−1)∪(2,4)∪(4,∞)
3. Find the intersection:
The intersection of these two sets is:
x∈(−2,−1)∪(2,3)
Step 4: Calculate the Probability
1. Length of the total solution set:
The total length of the solution set (−2,3) is:
3−(−2)=5
2. Length of the favorable solution set:
The length of the favorable solution set (−2,−1) is:
−1−(−2)=1
The length of the favorable solution set (2,3) is:
3−2=1
Thus, the total length of the favorable solution set is:
1+1=2
3. Calculate the probability:
The probability is given by the ratio of the length of the favorable cases to the total cases:
P=Length of favorable casesLength of total cases=25
Final Answer:
The probability that (x+1)(x−2)x−4≥0 for x selected from the solution set of the inequation y2−y−6≤0 is:
25
y2−y−6=(y−3)(y+2)≤0
The roots of the equation are y=3 and y=−2.
We will test the sign of the expression in the intervals defined by the roots:
- For y<−2: Choose y=−3 → (−)(−)>0
- For −2<y<3: Choose y=0 → (−)(+)<0
- For y>3: Choose y=4 → (+)(+)>0
The solution set where the expression is less than or equal to zero is:
y∈(−2,3)
We need to solve:
(x+1)(x−2)x−4≥0
The critical points are found by setting the numerator and denominator to zero:
- x+1=0 → x=−1
- x−2=0 → x=2
- x−4=0 → x=4
We will test the sign of the expression in the intervals defined by the critical points:
- For x<−1: Choose x=−2 → (+)(−)/(−)>0
- For −1<x<2: Choose x=0 → (+)(−)/(+)<0
- For 2<x<4: Choose x=3 → (+)(+)/(+)>0
- For x>4: Choose x=5 → (+)(+)/(+)>0
The solution set where the expression is greater than or equal to zero is:
x∈(−∞,−1)∪(2,4)∪(4,∞)
From Step 1, we have:
x∈(−2,3)
From Step 2, we have:
x∈(−∞,−1)∪(2,4)∪(4,∞)
The intersection of these two sets is:
x∈(−2,−1)∪(2,3)
The total length of the solution set (−2,3) is:
3−(−2)=5
The length of the favorable solution set (−2,−1) is:
−1−(−2)=1
The length of the favorable solution set (2,3) is:
3−2=1
Thus, the total length of the favorable solution set is:
1+1=2
The probability is given by the ratio of the length of the favorable cases to the total cases:
P=Length of favorable casesLength of total cases=25
The probability that (x+1)(x−2)x−4≥0 for x selected from the solution set of the inequation y2−y−6≤0 is:
25
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A natural number is selected at random from the set x={x:1≤x≤100}. The probability that the number satisfies the inequality x2 – 13x≤30 is______
A59B950C320D79 - Question 2 - Select One
The solution set of the inequalities 2x+y≥4,x+y≤x,2x−3y≤6 is
A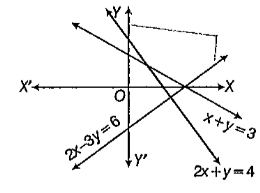 B
B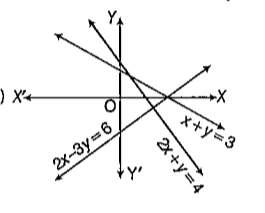 C
C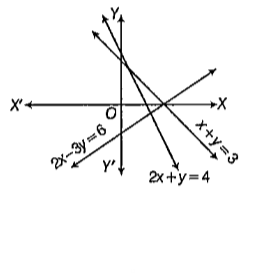 D
D
- Question 3 - Select One
Solution set of inequalities x−2y≥0,−2x−y+2≤0,x≥0,y≥0
AemptyBclosed half planeCinfiniteDfirst quadrant
Find the solutions set of inequalities 0≤x≤5,0≤2y≤7
View SolutionA natural number is selected at random from the set {1≤x≤100}. The probability that number satisfies the inequation x2+15≤16x, is :-
View SolutionDraw the graph of the solution set of the inequation 2x+y≥2,x−y≤1,x+2y≤8,x≥0andy≥0
View SolutionDraw the graph of the solution set of the system of inequations 2x+3y≤4,x≥0andy≥0.
View SolutionFind the area of the quadrilateral formed by the solution set of the inequations 2x+3y≤12,x0,y≥0 and x≤3.
View Solution

