A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?
To solve the problem step by step, we will follow the procedure outlined in the video transcript.
Step 1: Understand the Problem
We have a rhombus-shaped field with each side measuring 30 meters and the longer diagonal measuring 48 meters. We need to find out how much area of the field each of the 18 cows will get to graze.
Step 2: Calculate the Area of the Rhombus
The area of a rhombus can be calculated using the formula:
Area=12×d1×d2
where d1 and d2 are the lengths of the diagonals. We know one diagonal d1=48 m, but we need to find the other diagonal d2.
Step 3: Find the Length of the Other Diagonal
In a rhombus, the diagonals bisect each other at right angles. We can use the Pythagorean theorem to find the length of the other diagonal d2.
Let d2 be the length of the other diagonal. Each half of the diagonals will form two right triangles. The half of the longer diagonal is:
d12=482=24 m
Now, using the Pythagorean theorem in triangle formed by half diagonals and a side of the rhombus:
(d22)2+242=302
(d22)2+576=900
(d22)2=900−576=324
d22=√324=18 m
Thus, d2=2×18=36 m.
Step 4: Calculate the Area of the Rhombus
Now that we have both diagonals, we can calculate the area:
Area=12×48×36
Area=12×1728=864 m2
Step 5: Calculate the Area Available to Each Cow
To find the area available for each cow, we divide the total area by the number of cows:
Area per cow=864 m218
Area per cow=48 m2
Final Answer
Hence, the area grazed by each cow is 48 m².
---
We have a rhombus-shaped field with each side measuring 30 meters and the longer diagonal measuring 48 meters. We need to find out how much area of the field each of the 18 cows will get to graze.
The area of a rhombus can be calculated using the formula:
Area=12×d1×d2
where d1 and d2 are the lengths of the diagonals. We know one diagonal d1=48 m, but we need to find the other diagonal d2.
In a rhombus, the diagonals bisect each other at right angles. We can use the Pythagorean theorem to find the length of the other diagonal d2.
d12=482=24 m
Now, using the Pythagorean theorem in triangle formed by half diagonals and a side of the rhombus:
(d22)2+242=302
(d22)2+576=900
(d22)2=900−576=324
d22=√324=18 m
Thus, d2=2×18=36 m.
Now that we have both diagonals, we can calculate the area:
Area=12×48×36
Area=12×1728=864 m2
To find the area available for each cow, we divide the total area by the number of cows:
Area per cow=864 m218
Area per cow=48 m2
Hence, the area grazed by each cow is 48 m².
Similar Questions
If the area of a rhombus be 48 cm2 and one of its diagonals is 6 cm, find its altitude.
View SolutionSanya has a piece of land which is in the shape of a rhombus. She wants her one daughter and one son to work on the land and produce different crops to suffice the needs of their family. She divided the land in two equals parts. If the perimeter of the land is 400m and one of the diagonals is 160m, how much area each of them will get?
View Solution
Knowledge Check
Find the area of a rhombus having each side equal to 17 cm and one of its diagonal equal to 30 cm .
A440cm2.B340cm2.C240cm2.D540cm2.
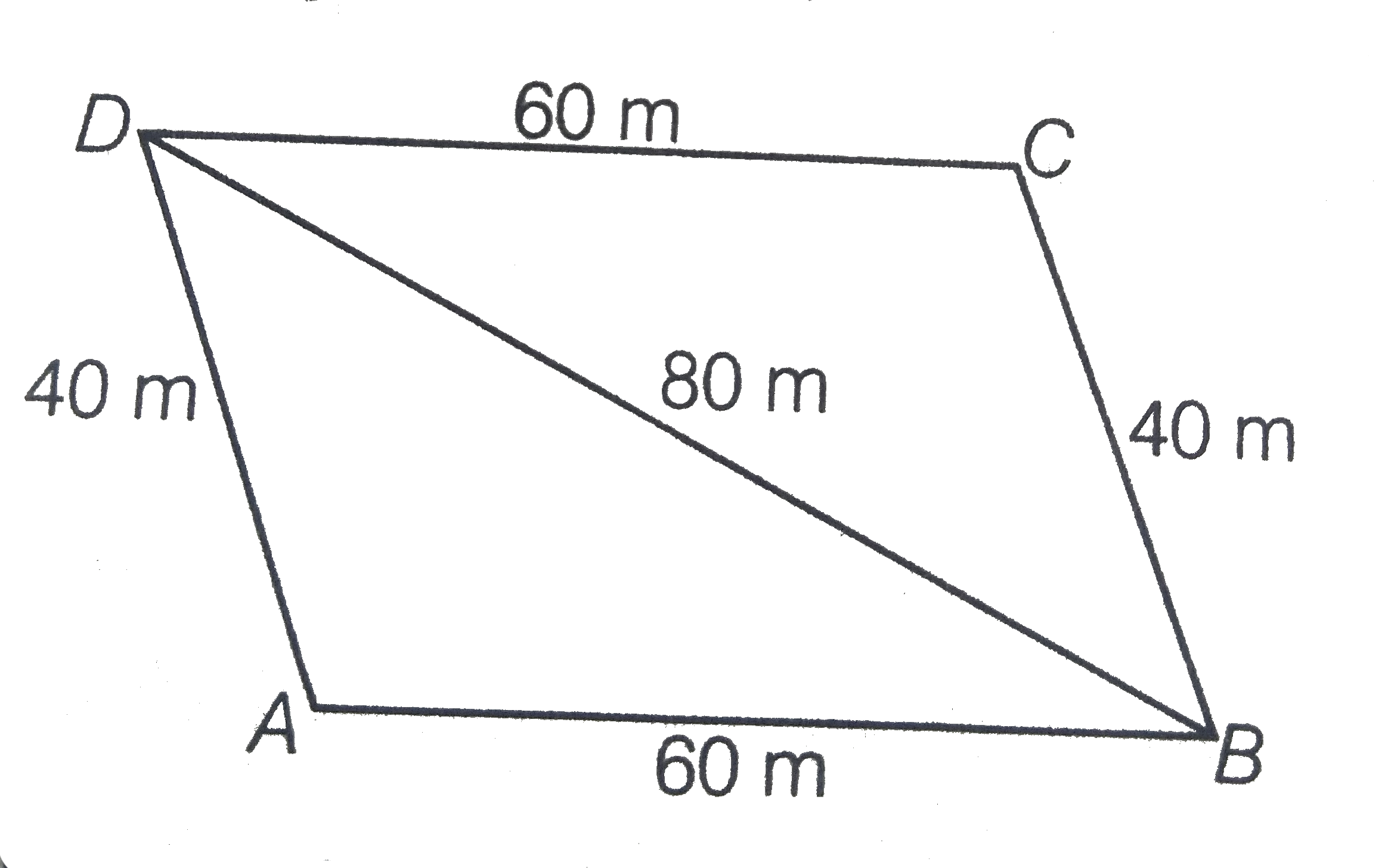
A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
View SolutionEach side of a rhombus is 18 cm. If the distance between two parallel sides is 12 cm, find its area.
View SolutionFind the area of a rhombus having each side equal to 20 cm and one of its diagonals equal to 24 cm .
View SolutionFind the area of a square field if its each side is 1034 m long.
View SolutionA field in the form of a rhombus has each side of length 64m and altitude 16m. What is the side of a square field which has the same area as that of a rhombus?
View SolutionSides of a triangular field are 15 m, 16m and 17m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
View SolutionFill in the blanks, in each of the following, so as to make the statement true: 1. A rhombus is a parallelogram in which.... 2. A square is a rhombus in which.... 3. A rhombus has all its sides of ........ length. 4. The diagonals of a rhombus..... each other at... angles. 5.It the diagonals of a parallelogram bisect each other at right angles, then it is a....
View Solution
