A rod of AB of length 3 rests on a wall as follows :

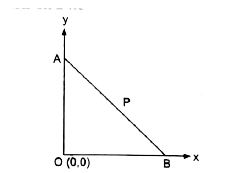
P is a point on AB such that $A P : P B = 1 : 2$ If the rod slides along the wall, then the locus of P lies on

A

$2 x + y + x y = 2$

B

$4 x^{2} + x y + x y + y^{2} = 4$

C

$4 x^{2} + y^{2} = 4$

D

$x^{2} + y^{2} - x - 2 y = 0$

Text Solution

Verified by Experts

The correct Answer is:C

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

BOOK - VK JAISWALCHAPTER - STRAIGHT LINES EXERCISE - Exercise-2 : One or More than One Answer is/are Correct
12videos
STRAIGHT LINES
BOOK - VK JAISWALCHAPTER - STRAIGHT LINES EXERCISE - Exercise-3 : Comprehension Type Problems
4videos
STRAIGHT LINES
BOOK - VK JAISWALCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-5 : Subjective Type Problems
13videos
SOLUTION OF TRIANGLES
BOOK - VK JAISWALCHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - Exercise-5 : Subjective Type Problems
9videos
TRIGONOMETRIC EQUATIONS

Similar Questions

Knowledge Check

Question 1 - Select One
Let ABCD be a square and let P be a point on AB such that $A P : P B = 1 : 2 . if ∠ A P D = θ$ , then what is the value of $cos θ$ ?
A $\frac{1}{\sqrt{10}}$
B $\frac{1}{\sqrt{5}}$
C $\frac{2}{\sqrt{10}}$
D $\frac{2}{\sqrt{5}}$
Question 2 - Select One
A point P moves such that PA/PB = p where A and B are two fixed pints with AB=a, the locus of P is a circle with radius
A $a . (1 - p^{2})$
B $p / (1 - a^{2})$
C $a p (1 - p^{2})$
D $a p / (1 - a^{2})$

VK JAISWAL-STRAIGHT LINES -Exercise-5 : Subjective Type Problems

Home
Ask Doubt
Profile