Question

A rod of length 2 units
whose one end is ${\displaystyle (1,0,-1)}$
and other end touches the plane ${\displaystyle x-2y=2Z+4=0,}$
then
a. the rod sweeps the figure whose volume is ${\displaystyle b.\pi c.}$
d.
cubic units.
e. the area of the region which the rod traces
on the plane is ${\displaystyle f.g.2\pi h.}$
i.

j.
the
length of projection of the rod on the plane is ${\displaystyle k.l.\sqrt{m.3n.}\odot p.}$
q.
units.
r. the centre of the region which the rod traces
on the plane is ${\displaystyle s.t.(u.v.w\frac{.2}{x}.3y.z.,aa\frac{.2}{b}b.3cc.dd.,-ee\frac{.5}{f}f.3gg.hh.ii.)\stackrel{.}{j}j.}$
kk.

Options

A. the rod sweeps the figure whose volume is `pi` cubic units.
B. the area of the region which the rod traces on the plane is `2pi`.
C. the length of projection of the rod on the plane is `sqrt3` units.
D. the centre of the region which the rod traces on the plane is `((2)/(3), (2)/(3), (-5)/(3))`

Answer

b

Explanation

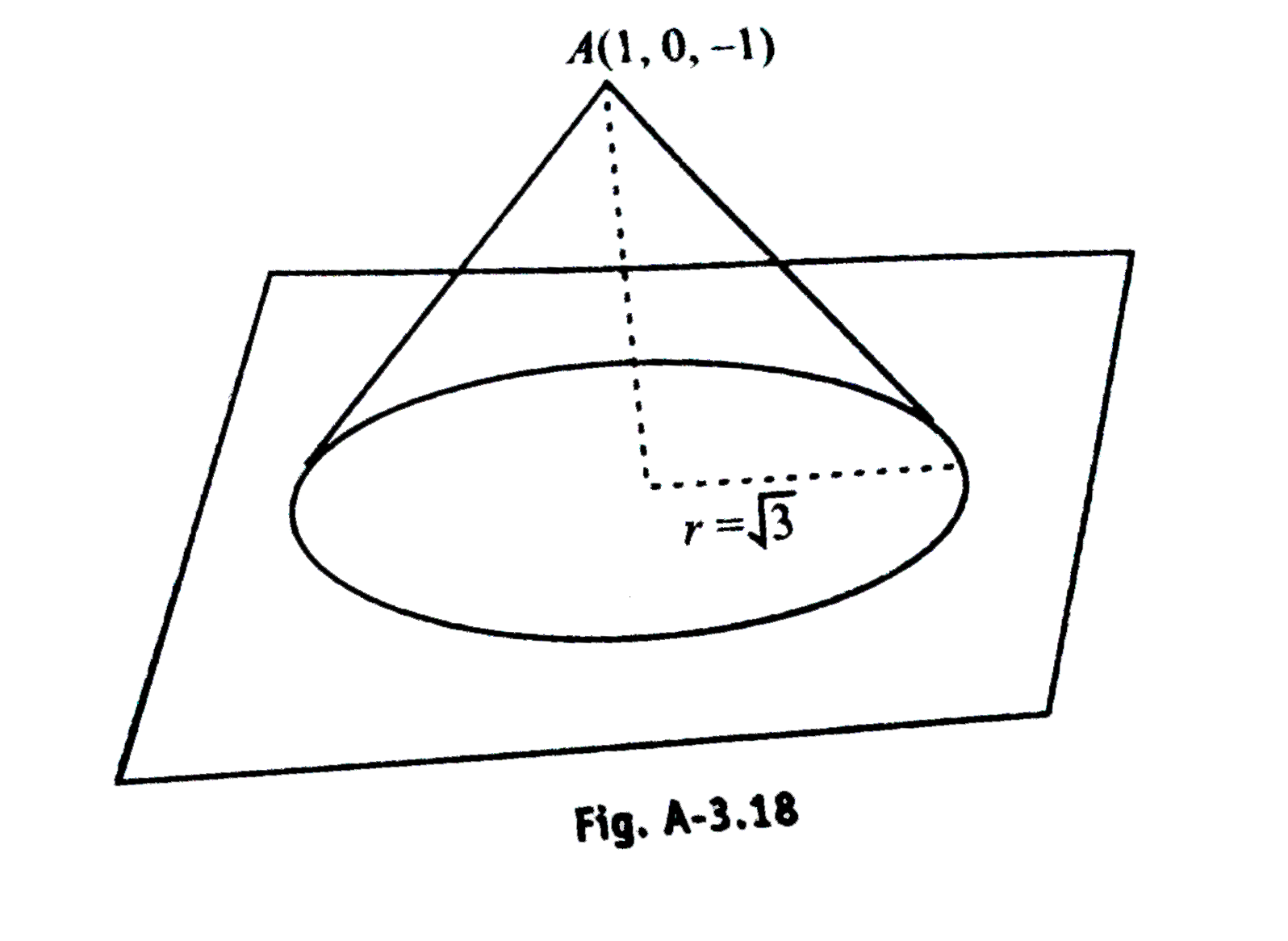
The rod sweeps out the figure which is a cone.
The distance of point `A(1, 0, -1)` from the plane is
`" "(|1-2+4|)/(sqrt9)=1` unit
The slant height `l` of the cone is 2 units.
Then the radius of the base of the cone is
`" "sqrt(l^(2)-1)= sqrt (4-1)= sqrt3`
Hence, the volume of the cone is
`" "(pi)/(3)(sqrt3)^(2)*1= pi ` cubic units
Area of the circle on the plane which the rod traces is `3pi`.
Also, the centre of the circle is `Q(x, y, z)`. Then
`" "(x-1)/(1)=(y-0)/(-2)= (z +1)/(2)= (-(1-0-2+4))/(1^(2)+ (-2)^(2) +2^(2))`
or `" "Q(x, y, z)-= ((2)/(3), (2)/(3), (-5)/(3))`.