Given four points A(2,1,0),B(1,0,1),C(3,0,1)andD(0,0,2). Point D lies on a line L orthogonal to the plane determined by the points A, B and C.
The equation of the plane ABC is Solution in Bengali
x+y+z−3=0
y+z−1=0
x+z−1=0
2y+z−1=0
The correct Answer is:b
∣∣
∣
∣∣x−2y−1z1−20−11−03−20−11−0∣∣
∣
∣∣=0
(x−2)[(−1)−(−1)]−(y−1)[(−1)−1]+z[1+1]=0
or 2(y−1)+2z=0
or y+z−1=0
The vector normal to the plane is →r=0ˆi+ˆj+ˆk
The equation of the line through (0,0,2) and parallel to →n is →r=2ˆk+λ(ˆj+ˆk)
The perpendicular distance of D(0,0,2) from plane
ABC is ∣∣
∣
∣∣2−1√12+12∣=1√2
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MATRIX-MATCH TYPE5videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - INTEGER TYPE10videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - REASONING TYPE10videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions291videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)4videos
TRIGONOMETRIC EQUATIONS
Similar Questions
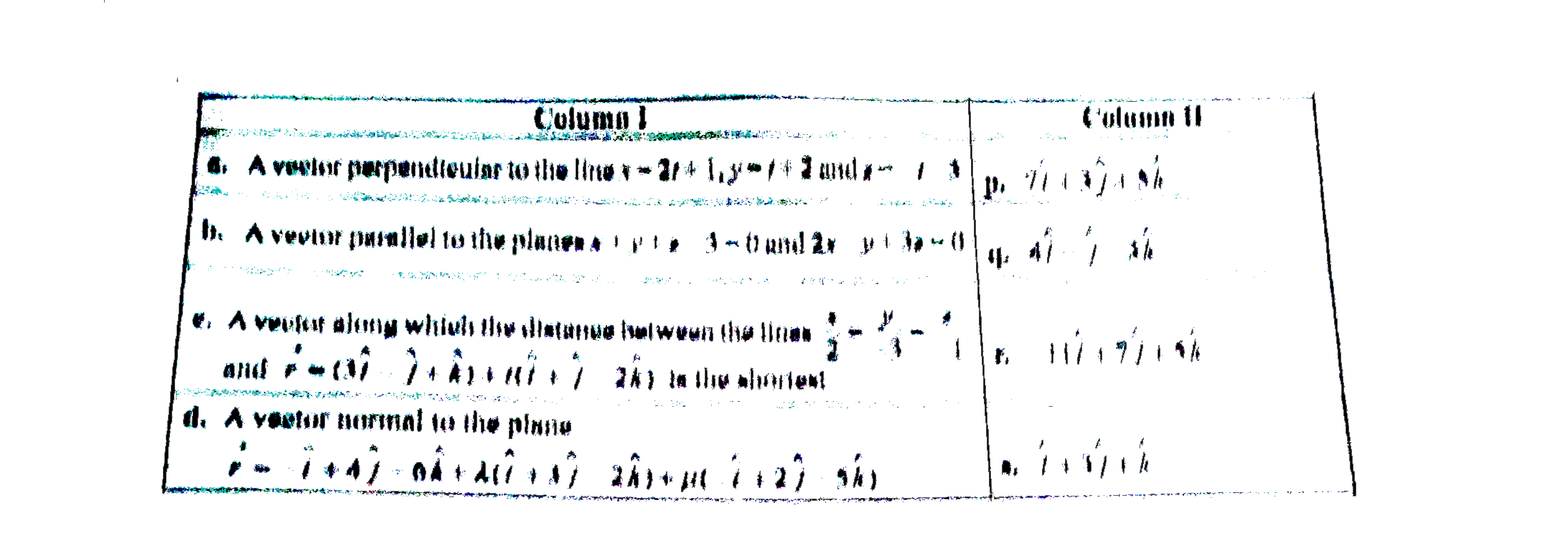01:16View SolutionFind the number of sphere of radius r touching the coordinate axes.
01:27View SolutionStatement 1: Lines →r=ˆi+ˆj−ˆk+λ(3ˆi−ˆj)and→r=4ˆi−ˆk+μ(2ˆi+3ˆk) intersect. Statement 2: →b×→d=0 , then lines →r=→a+λ→band→r=→c+λ→d do not intersect.
03:03View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
06:12View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
07:50View SolutionIf A(0+i0),B(-1+i)&C(1+i) are 3 points on argand plane,then the fourth point which forms the parallelogram can be (A) 2+i0(B)-2+0i(C)0+2i(D)-2i
06:15View SolutionIf points (a, 0), (0, b) and (1, 1) are collinear, then 1a+1b= (a) 1 (b) 2 (c) 0 (d) −1
View SolutionFind the equation of the plane through the points A(3, 2, 0), B(1, 3, -1) and C(0, -2, 3).
07:22View Solutionदिखाइए की बिंदु A(2, 1), B(0, 3), C(-2, 1) और D(0, -1) एक वर्ग के शीर्ष हैं ।
02:27View SolutionFind the coordiantes of the point in the xy-plane which is equiistant from the points A ( 0 , 0 , 1) , B ( 2 , 0 , 3) and C ( 0 , 3 , 2) .
10:00View SolutionXY - समतल पर वह बिंदु ज्ञात कीजिए जो बिंदुओं A (2 , 0 , 3) , B ( 0 , 3 , 2) तथा C ( 0 ,0 ,1) से समदूरस्थ है ।
05:18View Solutionदिखाइए की चार बिंदु A(0,−1,−1),B(4,5,1),C(3,9,4) और D(−4,4,4) समतलीय है| समतल का समीकरण ज्ञात कीजिए|
01:42View SolutionDetermine the point in yz plane which is equidistant from three points A(2, 0, 3), B(0, 3, 2) and C(0, 0, 1).
03:13View SolutionStatement 1: If point (α,β,γ) lies above the plane (a2+1)x+(b+1)y+(c2+c+1)z+d=0, then (a2+1)α+(b+1)β+(c2+c+1)γ+d>0.
because
Statement 2: If the point (α,β,γ) lies above the plane ax+by+cz+d=0 then aα+bβ+cγ+dc>0.03:20View SolutionGiven four points A(2,1,0)mB(1,2,3),C(3,1,1)andD(0,1,3). Point D lies on the line L which is perependicular to the plane determined by the points A, B, C. If the point of intersection of the plane determined by the points A, B, C and the line L is (a, b, c), then 9(a+b+c) is equal to
06:17View Solutionনীচের বিন্দুগুলির দ্বারা সমতলের সমীকরণ নির্ণয় করো: (3, 3, 0), (1, 1, 1) ও (0, -1, 0)
05:13View Solution