A rod of length l cm moves with its ends A (on x=-axis) and B (on y-axis) always touching the coordinae axes. Prove that the point P on the rod which divides AB in the ratio λ(≠1) is ellipse. Alos, find the eccentricity of the ellipse. Solution in Bengali
From the figure,
In ΔPQB,cosθ=PQPB=hPA
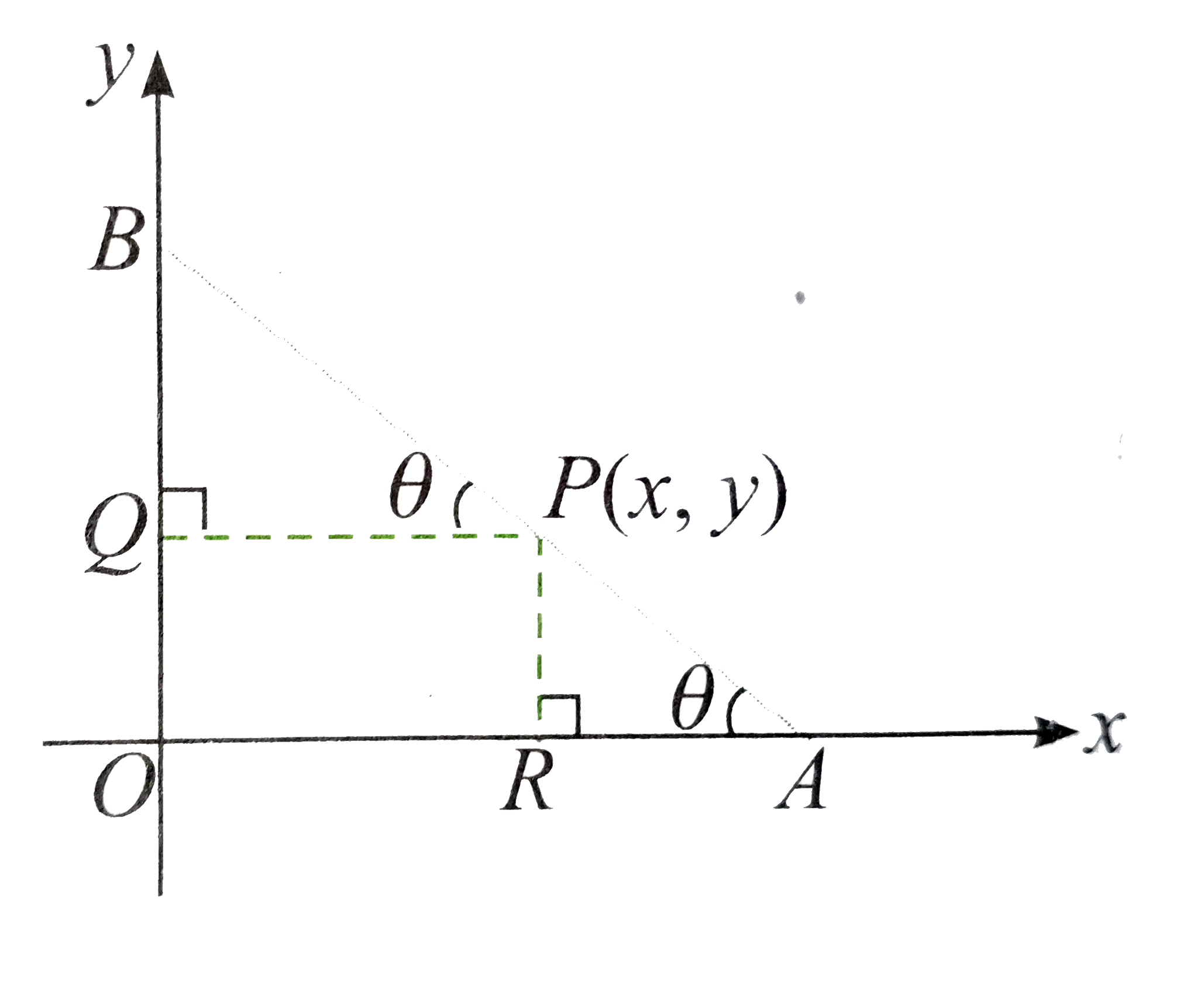
Now, APPA=λ1
⇒APλ=PB1=AP+PBλ+1=ABλ+1=lλ+1
∴AP=λlλ+1andPB=lλ+1
∴cosθ=h(λ+1)l=andsinθ=k(λ+1)λl
Squaring and adding,
h2(λ+1)2l2+k2(λ+1)2λ2l2=1
or x2l2(λ+1)2+y2λ2l2(λ+1)2=1
This is the equation of required locus, Clrarly this is the eqution of ellipse.
Let λ<1, then e2=1−λ2l2(λ+1)2l2(λ+1)2=1−λ2
∴e=√1−λ2
Similar Questions
A rod AB of length 15 cm rests in between two coordinate axes is such a way that the end point A lies on x-axis and end Point B lies on y-axis. A point P (x,y) is taken on the rod in such a way that AP=6cm . Show that the locus of P is an ellipse.
View SolutionA rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with the x-axis.
View SolutionA rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3cm from the end in contact with the x-axis.
View SolutionA rod of length l cm moves with its ends A (on x=-axis) and B (on y-axis) always touching the coordinae axes. Prove that the point P on the rod which divides AB in the ratio λ(≠1) is ellipse. Alos, find the eccentricity of the ellipse.
View SolutionA rod AB of length 15cm rests in between two coordinate axes in such a way that the end point A lies on x−axis and end point B lies on y-axis . A point is taken on the rod in such a way that AP=6cm . Show that the locus of P is an ellipse. Also find its eccentricity.
View SolutionA rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3cm from the end in contact with the x-axis.
View SolutionA rod of length 12 cm moves with its ends always touching the co-ordinates axes. Determine the equations of the locus of a point P on the rod, which is 3cm from the end in contact with the x-axis
View SolutionA rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3cm from the end in contact with the x-axis.
View Solution
