A sector of a circle of radius 12 cm has the angle 120∘ It is rolled up so that two bounding radii are joined together to form a cone. Find the volume of the cone.
189.6cm3
169.5cm3
179.6cm3
125.5cm3
The correct Answer is:A
To find the volume of the cone formed by rolling up a sector of a circle with a radius of 12 cm and an angle of 120 degrees, we can follow these steps:
Step 1: Find the Length of the Arc of the Sector
The length of the arc (L) of the sector can be calculated using the formula:
L=θ360×2πr
where:
- θ=120∘
- r=12cm
Substituting the values:
L=120360×2π×12
L=13×2π×12
L=8πcm
Step 2: Relate the Length of the Arc to the Circumference of the Base of the Cone
When the sector is rolled up to form a cone, the length of the arc becomes the circumference (C) of the base of the cone:
C=L=8πcm
The circumference of the base of the cone can also be expressed as:
C=2πr
where r is the radius of the base of the cone. Setting the two equations for circumference equal gives:
2πr=8π
Step 3: Solve for the Radius of the Base of the Cone
Dividing both sides by 2π:
r=8π2π=4cm
Step 4: Find the Height of the Cone
The radius of the original sector (which becomes the slant height l of the cone) is 12 cm. We can use the Pythagorean theorem to find the height h of the cone:
l2=r2+h2
Substituting the known values:
122=42+h2
144=16+h2
h2=144−16=128
h=√128=8√2cm
Step 5: Calculate the Volume of the Cone
The volume V of the cone can be calculated using the formula:
V=13πr2h
Substituting the values:
V=13π(4)2(8√2)
V=13π(16)(8√2)
V=128√23πcm3
Final Answer
The volume of the cone is:
V=128√23πcm3
---
The length of the arc (L) of the sector can be calculated using the formula:
L=θ360×2πr
where:
- θ=120∘
- r=12cm
L=120360×2π×12
L=13×2π×12
L=8πcm
When the sector is rolled up to form a cone, the length of the arc becomes the circumference (C) of the base of the cone:
C=L=8πcm
C=2πr
where r is the radius of the base of the cone. Setting the two equations for circumference equal gives:
2πr=8π
Dividing both sides by 2π:
r=8π2π=4cm
The radius of the original sector (which becomes the slant height l of the cone) is 12 cm. We can use the Pythagorean theorem to find the height h of the cone:
l2=r2+h2
Substituting the known values:
122=42+h2
144=16+h2
h2=144−16=128
h=√128=8√2cm
The volume V of the cone can be calculated using the formula:
V=13πr2h
Substituting the values:
V=13π(4)2(8√2)
V=13π(16)(8√2)
V=128√23πcm3
The volume of the cone is:
V=128√23πcm3
Topper's Solved these Questions
- SURFACE AREAS AND VOLUMES BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - Everday Mathematics
4 Videos
- SURFACE AREAS AND VOLUMES BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - Achievers section (Hots)
3 Videos
- STATISTICS BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - STATISTICS EXERCISE - Achievers section (Hots)
3 Videos
- TRIANGLESBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - TRIANGLESEXERCISE - ACHIEVERS SECTION (HOTS)
5 Videos
Similar Questions
A sector of a circle of radius 15 cm has the angle 120∘. It is rolled up so that two bounded radii are joined together to form a cone. Find the volume of the cone. (Take π = 22/7)

View SolutionA sector of a circle of radius 6 cm and central angle 30∘ is folded into a cone such that the radius of the sector becomes the slant height of the cone. What is the radius of the base of the cone thus formed?
View Solution
Knowledge Check
A right angled sector of radius r cm is rolled up into a cone in such a way that the two binding radii are joined together. Then the curved surface area of the cone is
Aπr2cm2B4πr2cm2Cπr24cm2D2πr2cm2A circle is drawn in a sectore of a larger circle of radius r, as shown in fugure. The smaller circle is tangent to the two bounding radii and the are of the sector. The radius of the smaller circle is
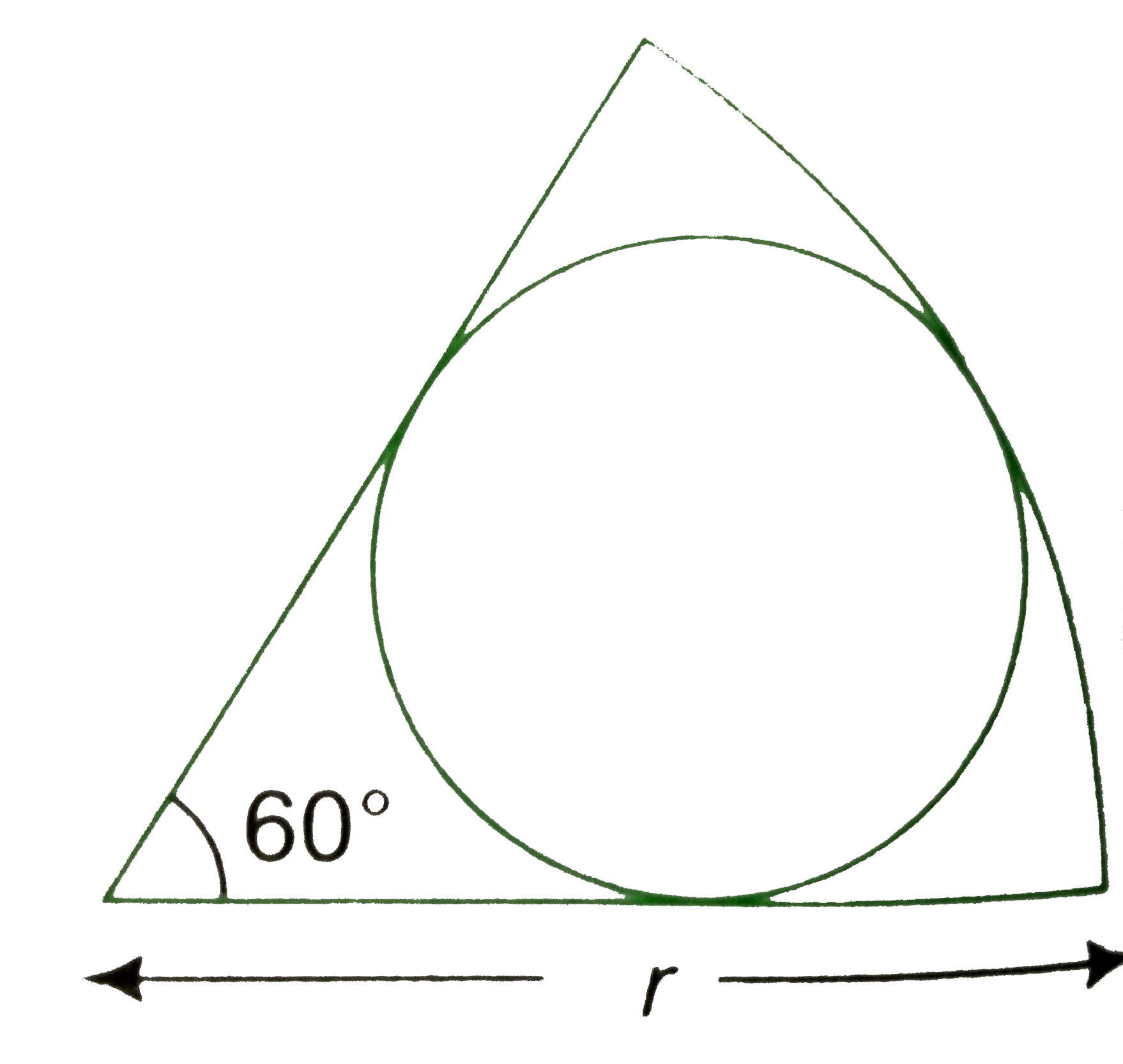 Ar2Br3C2√3r5Dr√2
Ar2Br3C2√3r5Dr√2The radius of the base of a cone is 21 cm and the height is 20 cm. Find the volume the cone
A8460cm3B9240cm3C4620cm3D3230cm3
A sector of radius 10.5 cm with the central angle 120∘ is folded to form a cone by joining the two bounding radii of the sector. What is the volume (in cm3 ) of the cone so formed ?
10.5 सेमी त्रिज्या वाला एक वृत्त खंड है जिसका केंद्रीय कोण 120∘ है | इसे मोड़कर वृत्त खंड की दो सीमांकन त्रिज्याओं को जोड़ कर एक शंकु का निर्माण किया जाता है | इस प्रकार निर्मित शंकु का आयतन ( घन सेमी में) क्या होगा ?
View SolutionIf the sector of a circle with radius 10 cm has central angle 18∘, find the area of the sector. (π=3.14)
View SolutionIf the sector of a circle with radius 10 cm has central angle 72∘, find the area of the sector. (π=3.14)
View SolutionFor a cone ,radius =1.4 cm and height =6cm . Find the volume of the cone. (π=227)
View SolutionA sector is cut-off from a circle of radius 21 cm. The angle of the sector is 120o . Find the length of its arc and the area.
View Solution
