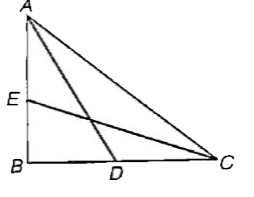
In figure, ABC is a right triangle, right angled at B. AD and CE are the two medians drawn from A and C respectively. If AC = 5 cm and AD=3√52cm, find the length of CE:
4 cm
2√5 cm
3√5 cm
5 cm
The correct Answer is:B
Step by step video, text & image solution for In figure, ABC is a right triangle, right angled at B. AD and CE are the two medians drawn from A and C respectively. If AC = 5 cm and AD=(3sqrt5)/(2)cm, find the length of CE: by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
In Fig. 4.192, ABC is a right triangle right-angled at B . AD and CE are the two medians drawn from A and C respectively. If AC=5cm and AD=3√52cm , find the length of CE . (FIGURE)
View SolutionABC is right triangle right angled at B.If BD is the length of the perpendicular drawn from B to AC then
View Solution
Knowledge Check
- Question 1 - Select One
In figure, ABC is a right triangle, right angled at B. AD and CE are the two medians drawn from A and C respectively. If AC = 5 cm and AD=3√52cm, find the length of CE:
 A2 cmB2√5 cmC5√2 cmD3√2 cm
A2 cmB2√5 cmC5√2 cmD3√2 cm - Question 2 - Select One
In Δ ABC, DE || AC, D and E are two points on AB and CB respectively, If AB=10 cm and AD =4 cm, then BE : CE is
A2:3B2:5C5:2D3:2 - Question 3 - Select One
ΔABC is right-angled at C. If AC=5cmandBC=12cm find the length of AB.
A17B7C13D14
In the given figure , ABC is a right triangle, right angled at B. Medians AD and CE are of respective length 5 cm and 2√5cm . Find the length of AC.
 View Solution
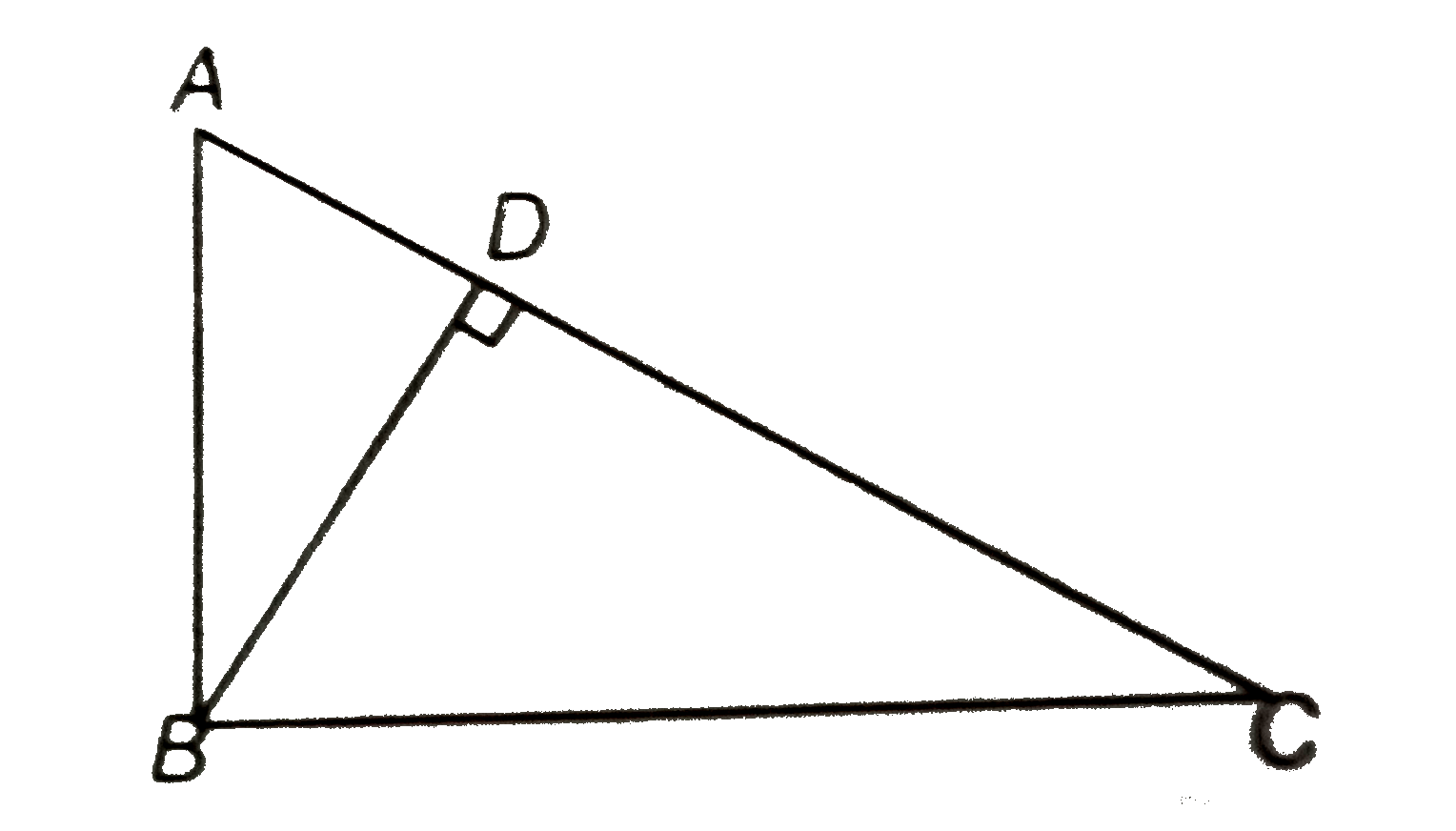
View SolutionIn given figure, ABC is a triangle right angled at B and BD⊥AC. If AD=4 cm and CD= 5 cm, then find BD and AB.
 View Solution
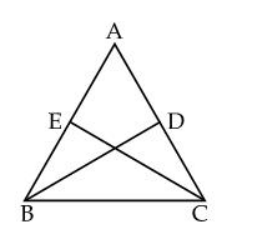
View SolutionIn Figure, ABC is an isosceles triangle with AB=AC, BD and CE are two medians of the triangle. Prove that BD=CE
 View Solution
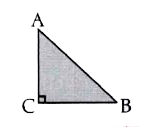
View SolutionIn Figure ABC is an isosceles triangle right angled at C with AC = 4 cm . Find the length of AB .
 View Solution
View SolutionIn Figure, ABC is a right triangle right angled at B and points DandE trisect BC . Prove that 8AE2=3AC2+5AD2.
View Solution

