A small firm manufactures items A and B. The total number of items that it can manufacture in a day is at the most 24 Item A takes on hour to make while item B takes only half an hour. The maximum time available per day is 16 hours. If the profit on one unit of item A be 300 and that on one unit of item B be 160, how many of each type of item should be produced to maximize the profit? Solve the problem graphically
Z is maximum at (9,18) and its maximum value is Rs. 3898.
Z is maximum at (7,17) and its maximum value is Rs. 4998.
Z is maximum at (9,15) and its maximum value is Rs. 4860.
Z is maximum at (8,16) and its maximum value is Rs. 4960.
The correct Answer is:D
Let x items of A and y items of B be produced. Then, x+y≤24,1x+12.y≤16,x≥0andy≥0.
Maximize P=300x+160y.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - RS AGGARWALCHAPTER - LINEAR PROGRAMMINGEXERCISE - EXPRCISE 33B (LONG-ANSWER QUESTIONS)
3 Videos
- LINEAR PROGRAMMINGBOOK - RS AGGARWALCHAPTER - LINEAR PROGRAMMINGEXERCISE - SECTION A
4 Videos
- LINEAR PROGRAMMINGBOOK - RS AGGARWALCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exprcise 33A
11 Videos
- LINEAR DIFFERENTIAL EQUATIONS BOOK - RS AGGARWALCHAPTER - LINEAR DIFFERENTIAL EQUATIONS EXERCISE - Objective Questions
27 Videos
- MATRICESBOOK - RS AGGARWALCHAPTER - MATRICESEXERCISE - Exercise 5F
21 Videos
Similar Questions
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes 1 hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300, how many of each should be produced daily to maximize the profit?
View SolutionA small firm manufactures gold rings and chains. The total number of rings and chains manufactured per day is atmost 24. It takes 1 hour to make a ring and 30 minutes to make a chain. The maximum number of hours available per day is 16. If the profit on a ring is Rs. 300 and that on a chain is Rs. 190, find the number of rings and chains that should be manufactured per day, so as to earn the maximum profit. Make it as an L.P.P. and solve it graphically.
View Solution
Knowledge Check
A small firm manufactures necklaces & bracelets . The combined number of necklaces and bracelets that it can handle per day is at most 24 . A bracelet takes 1 hour to make and a necklace takes half an hour . The maximum number of hours available per day is 16 . If the profit on a bracelet is Rs 300 and the profit on a necklace is Rs 100 , then form LPP to maximize the profit.
AMaximize z=100x+300y subject to x≥0,y≥0,x+2y≤32,x+y≤24.BMaximize z=100x+300y subject to x≥0,y≥0,x+2y≤32,x+y≥24.CMaximize z=100x+300y subject to x≥0,y≥0,x+2y≥32,x+y≥24.DMaximize z=100x+300y subject to x≥0,y≥0,x+2y≥32,x+y≤24.
Match the items of A and B

View SolutionA small firm manufactures neclaces and bracelets.The total number of neclaces and bracelets that it can handle per day is at most 24.It takes one hour to make a bracelet and half an hour to make a neclace.The maxium number of hours available per day is 16. If the profit on a neclace is ₹ 100 and that on a braclet is ₹ 300. Formulate an LLP for finding how many of each should be produced daily to maximize the profit? It is being given that at least one of ecah must be produced.
View SolutionA small firm manufactures gold rings and chains. The total number of rings and chains manufactured per day is atmost 24. It takes 1 hour to make a ring and 30 minutes to make a chain. The maximum number of hours available per day is 16. If the profit on a ring is Rs. 300 and that on a chain is Rs 190, find the number of rings and chains that should be manufactured per day, so as to earn the maximum profit. Make it as an L.P.P. and solve it graphically.
View SolutionIf 5 items cost Rs. a, the number of items that can be bought for Rs. b is ..
View SolutionA factory makes two types of items A and B, made of plywood. One piece of item A requires 5 minutes for cutting and 10 minutes for assembling. One piece of item B requires 8 minutes for cutting and 8 minutes for assembling. There are 3 hours and 20 minutes available for cutting and 4 hours for assembling. The profit on one piece of item A is Rs 5 and that on item B is Rs 6. How many pieces of each type should the factory make so as to maximise profit? Make it as an L.P.P. and solve it graphically.
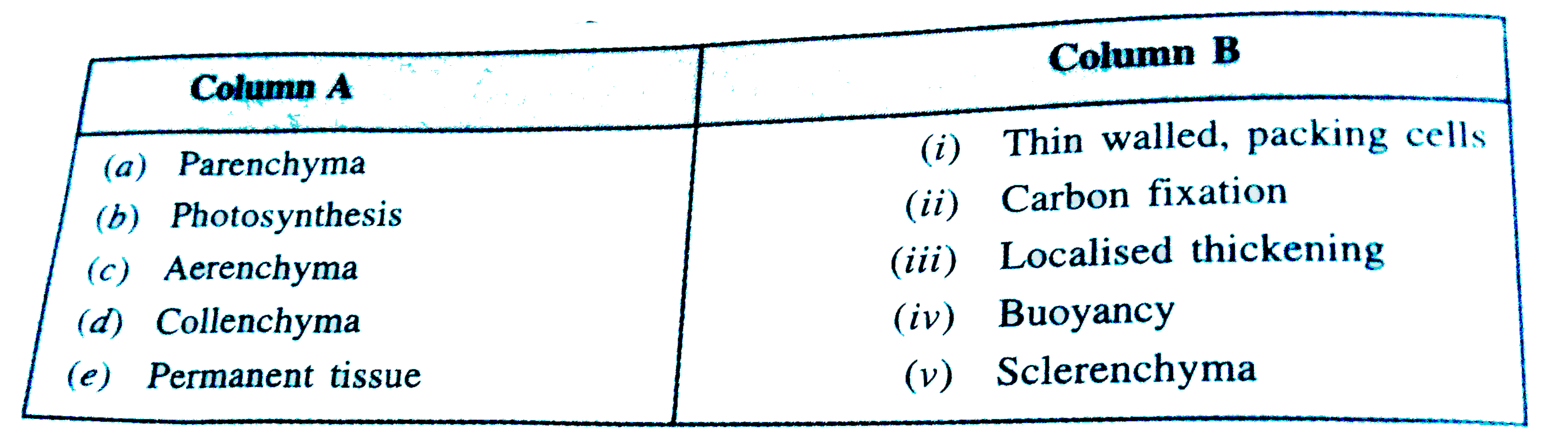
View SolutionMatch the items of column A and B
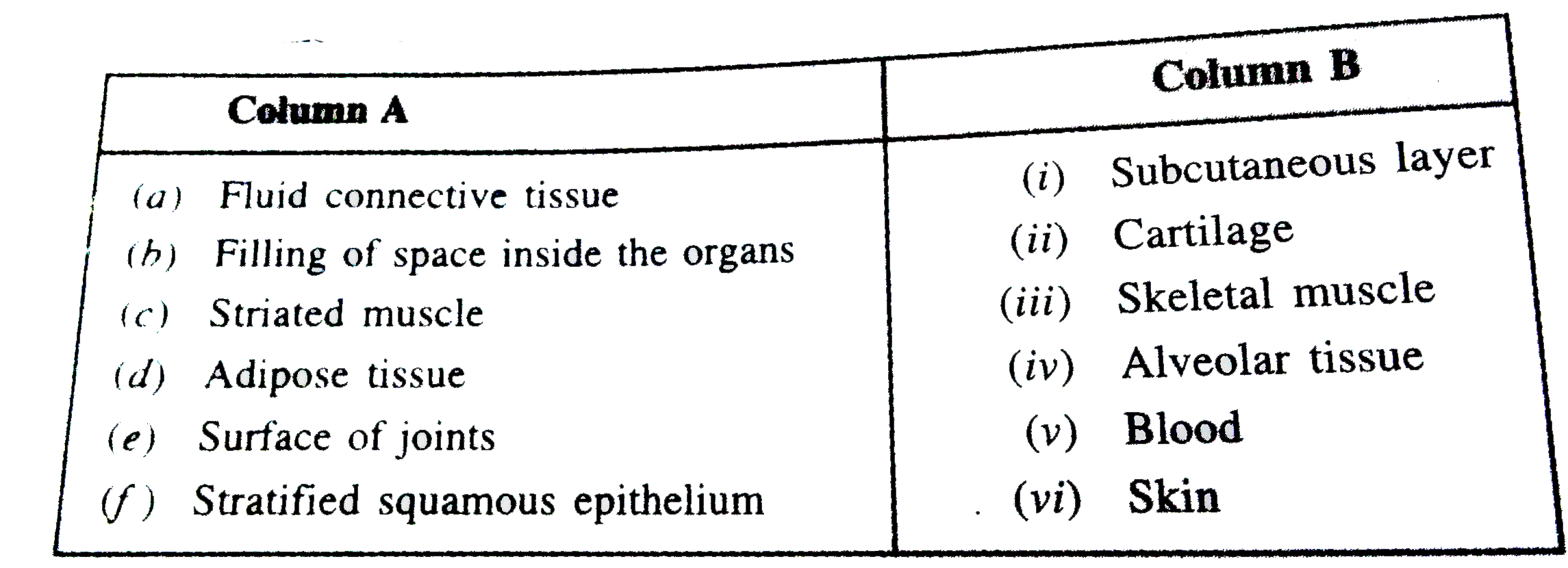
View SolutionMatch the items of colume A and column B.
View Solution
