A solid, cone-shaped lead crystal paper weight has a height of 5 centimeters and a base diameter that is 20% larger than the height. If the density of lead crystal is 3.1g/cm3, what is the approximate mass of the paperweight? Round your answer to the nearest gram.
The correct Answer is:A, D
To find the mass of the cone-shaped lead crystal paperweight, we will follow these steps:
Step 1: Determine the height and diameter of the cone
The height of the cone is given as 5 cm. The base diameter is 20% larger than the height.
Calculation:
Diameter=Height+0.2×Height=1.2×Height=1.2×5cm=6cm
Step 2: Calculate the radius of the base
The radius is half of the diameter.
Calculation:
Radius=Diameter2=6cm2=3cm
Step 3: Calculate the volume of the cone
The formula for the volume V of a cone is:
V=13πr2h
Substituting the values of radius and height:
V=13π(3cm)2(5cm)=13π(9cm2)(5cm)=13π(45cm3)
Step 4: Simplify the volume
Calculating the volume:
V=15πcm3
Step 5: Calculate the mass using density
The mass m can be calculated using the formula:
m=Density×Volume
Given that the density of lead crystal is 3.1g/cm3:
m=3.1g/cm3×15πcm3
Step 6: Calculate the numerical value
Using π≈3.14:
m=3.1×15×3.14≈3.1×47.1≈146.01g
Step 7: Round the mass to the nearest gram
Rounding 146.01g gives:
m≈146g
Thus, the approximate mass of the paperweight is 146 grams.
---
The height of the cone is given as 5 cm. The base diameter is 20% larger than the height.
Diameter=Height+0.2×Height=1.2×Height=1.2×5cm=6cm
The radius is half of the diameter.
Radius=Diameter2=6cm2=3cm
The formula for the volume V of a cone is:
V=13πr2h
Substituting the values of radius and height:
V=13π(3cm)2(5cm)=13π(9cm2)(5cm)=13π(45cm3)
Calculating the volume:
V=15πcm3
The mass m can be calculated using the formula:
m=Density×Volume
Given that the density of lead crystal is 3.1g/cm3:
m=3.1g/cm3×15πcm3
Using π≈3.14:
m=3.1×15×3.14≈3.1×47.1≈146.01g
Rounding 146.01g gives:
m≈146g
Topper's Solved these Questions
Similar Questions
Davis drew a unit circle and labeled the cosine and sine of 45∘ as (√22,√22). As suming that Davis is correct, which of the following statements must be true?
02:42View SolutionIf a function p(x) has four distinct zeros, which of the following could represent the entire graph of p in a standard coordinate plane?
05:09View SolutionThe density of lead is approximately 0.41 pounds per cubic inch. What is the approximately mass, in pounds, of a lead ball that has a 5 inch diameter?
02:35View Solutionஉயரம் 2.4செ.மீ மற்றும் விட்டம் 1.4செ.மீ கொண்ட ஒரு திண்ம உருளையில் இருந்து அதேவிட்டமும் உயரமும் உள்ள ஒரு கூம்பு வெட்டி எடுக்கப்பட்டால் மீதமுள்ள திண்மத்தின் கனஅளவு எவ்வளவு கன செ.மீ ஆகும்? .
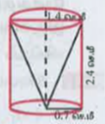 03:15View Solution
03:15View SolutionA hemispherical of lead of diameter 14 cm is cast into a right circular cone of height 14 cm. The radius of the base of the cone is :
02:58View SolutionThe diameter of a lead ball is 2.1 cm The density of the lead used is 11.34g/c3 What is the weight of the ball ?
View SolutionThe diameter of a lead ball is 2.1 cm The density of the lead used is 11.34g/c3 What is the weight of the ball ?
02:20View SolutionThe diameter of a lead ball is 2.1 cm The density of the lead used is 11.34g/c3 What is the weight of the ball ?
02:02View SolutionThe diameter of a lead ball is 2.1 cm The density of the lead used is 11.34g/c3 What is the weight of the ball ?
04:26View SolutionThe diameter of a lead ball is 2.1 cm The density of the lead used is 11.34g/c3 What is the weight of the ball ?
02:35View Solutionএকটি নিরেট লম্ব বৃত্তাকার শঙ্কুর উচ্চতা 25 সেমি. এবং তির্যক উচ্চতা 20 সেমি.। শঙ্কুটির সমান আয়তনবিশিষ্ট একটি নিরেট লম্ব বৃত্তাকার চোঙের উচ্চতা 5 সেমি. হলে, চোঙটির ভুমিতলের ব্যাসের দৈর্ঘ্য হিসাব করো।
02:33View SolutionA hemispherical of lead of diameter 14 cm is cast into a right circular cone of height 14 cm. The radius of the base of the cone is :
02:34View Solutionএকটি নিরেট লম্ব বৃত্তাকার শঙ্কুর উচ্চতা 20 সেমি এবং তির্যক উচ্চতা 25 সেমি, শঙ্কুটির সমান আয়তনবিশিষ্ট একটি নিরেট লম্ব বৃত্তাকার চোঙের উচ্চতা 15 সেমি হলে, চোঙের ভূমিতলের ব্যাস কত?
01:37View Solutionदो लंब वृताकार शंकु, जिनकी ऊँचाई एक समान है और जिनके आधारों की त्रिज्या 3 सेमी तथा 4 सेमी है, एक साथ लाकर 5 सेमी वाले एक ठोस गोले में बदल जाते हैं। तदनुसार, शंकु की ऊँचाई कितनी होगी?
01:30View Solution6 सेमी व्यास की एक ठोस धात्विक गोल बालको पिपलाकर पुनः ढाला जाता है और शंकु का आकार दिया जाता है जिसके आधार (बेस) का व्यास 12 सेमी है। शंकु की ऊंचाई बताएँ।
02:49View Solution

