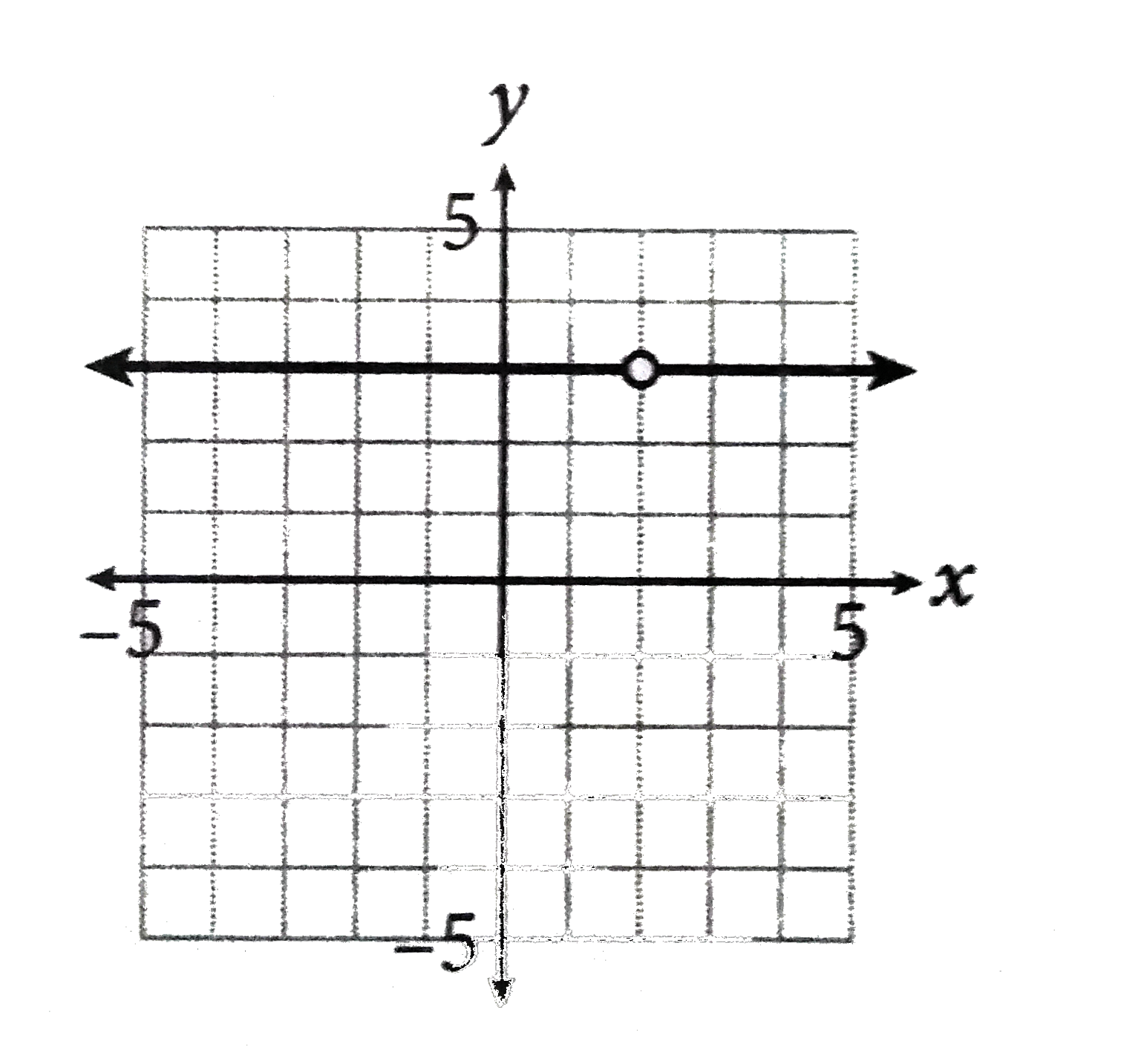
If a function p(x) has four distinct zeros, which of the following could represent the entire graph of p in a standard coordinate plane?


The correct Answer is:D
To solve the problem, we need to determine which graph represents a function p(x) that has four distinct zeros. A zero of a function is a value of x for which p(x)=0, and graphically, these zeros correspond to the points where the graph intersects the x-axis.
1. Understand the Concept of Zeros:
- Zeros of a function are the x-values where the function equals zero. In a graph, these are the points where the graph crosses the x-axis.
2. Identify the Requirement:
- We need to find a graph that intersects the x-axis at four distinct points. This means the graph must have four separate x-intercepts.
3. Analyze the Options:
- We will evaluate each option to see how many times it intersects the x-axis.
4. Evaluate Option A:
- Check how many times the graph intersects the x-axis.
- Result: It intersects the x-axis only two times.
- Conclusion: This option does not have four distinct zeros.
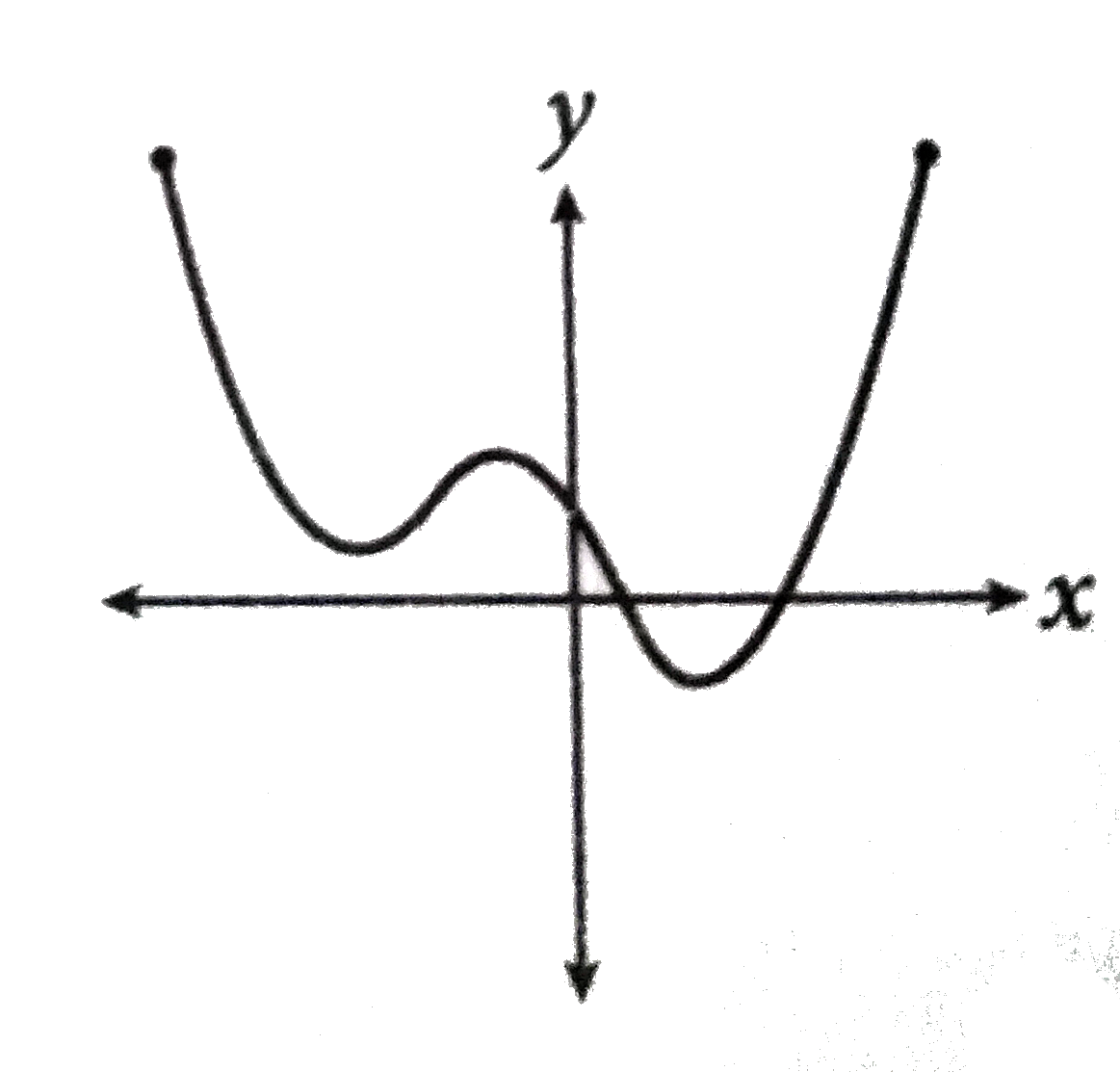
5. Evaluate Option B:
- Check how many times the graph intersects the x-axis.
- Result: It intersects the x-axis three times.
- Conclusion: This option does not have four distinct zeros.
6. Evaluate Option C:
- Check how many times the graph intersects the x-axis.
- Result: It intersects the x-axis two times.
- Conclusion: This option does not have four distinct zeros.
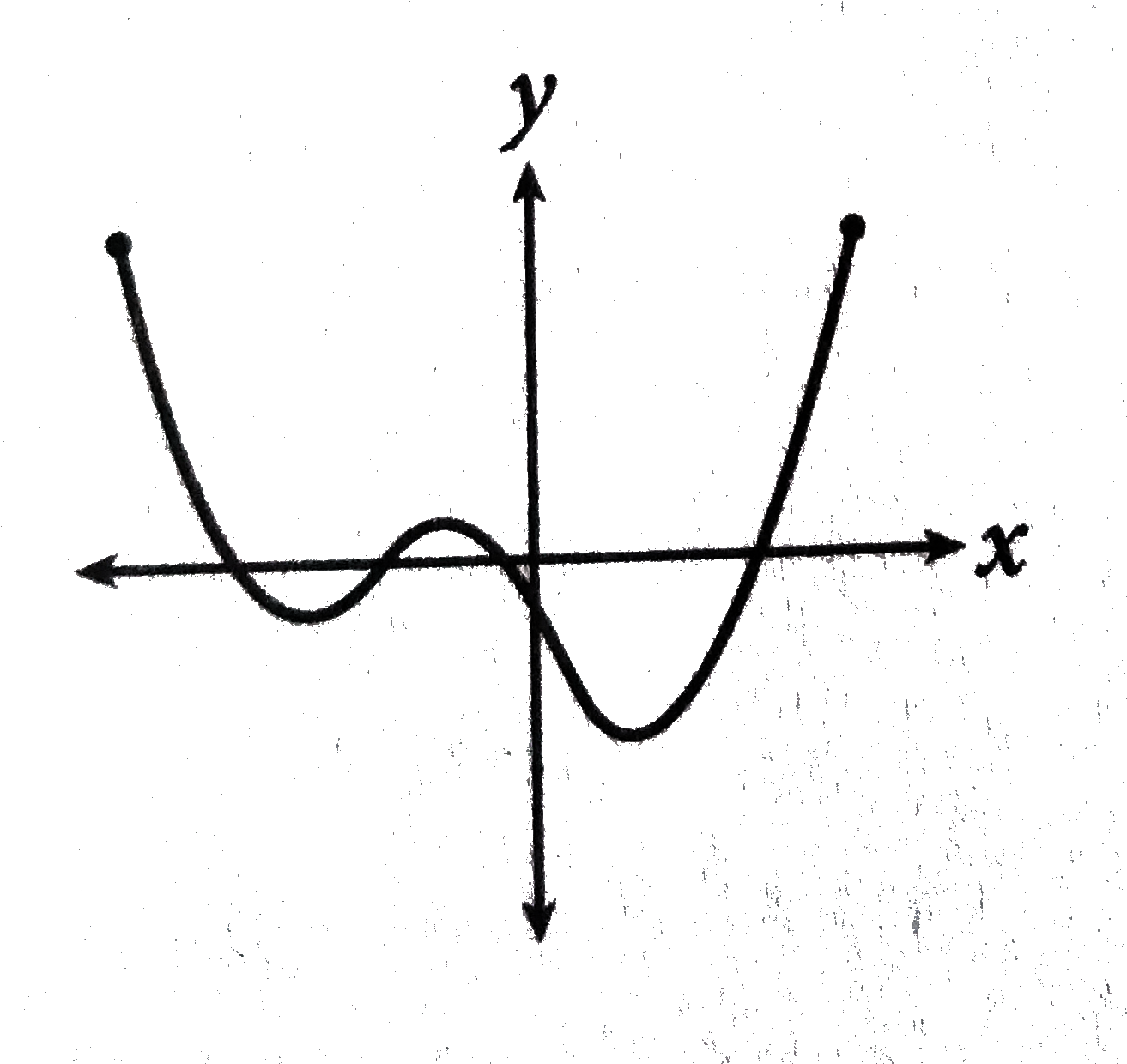
7. Evaluate Option D:
- Check how many times the graph intersects the x-axis.
- Result: It intersects the x-axis four times.
- Conclusion: This option has four distinct zeros.
8. Final Decision:
- Since only Option D intersects the x-axis four times, it is the correct representation of the function p(x) with four distinct zeros.
Conclusion:
The correct answer is Option D.
- Zeros of a function are the x-values where the function equals zero. In a graph, these are the points where the graph crosses the x-axis.
- We need to find a graph that intersects the x-axis at four distinct points. This means the graph must have four separate x-intercepts.
- We will evaluate each option to see how many times it intersects the x-axis.
- Check how many times the graph intersects the x-axis.
- Result: It intersects the x-axis only two times.
- Conclusion: This option does not have four distinct zeros.
- Check how many times the graph intersects the x-axis.
- Result: It intersects the x-axis three times.
- Conclusion: This option does not have four distinct zeros.
- Check how many times the graph intersects the x-axis.
- Result: It intersects the x-axis two times.
- Conclusion: This option does not have four distinct zeros.
- Check how many times the graph intersects the x-axis.
- Result: It intersects the x-axis four times.
- Conclusion: This option has four distinct zeros.
- Since only Option D intersects the x-axis four times, it is the correct representation of the function p(x) with four distinct zeros.
The correct answer is Option D.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If the function f has three distinct zeros, which of the following represents the graph of f in the xy-plane?
A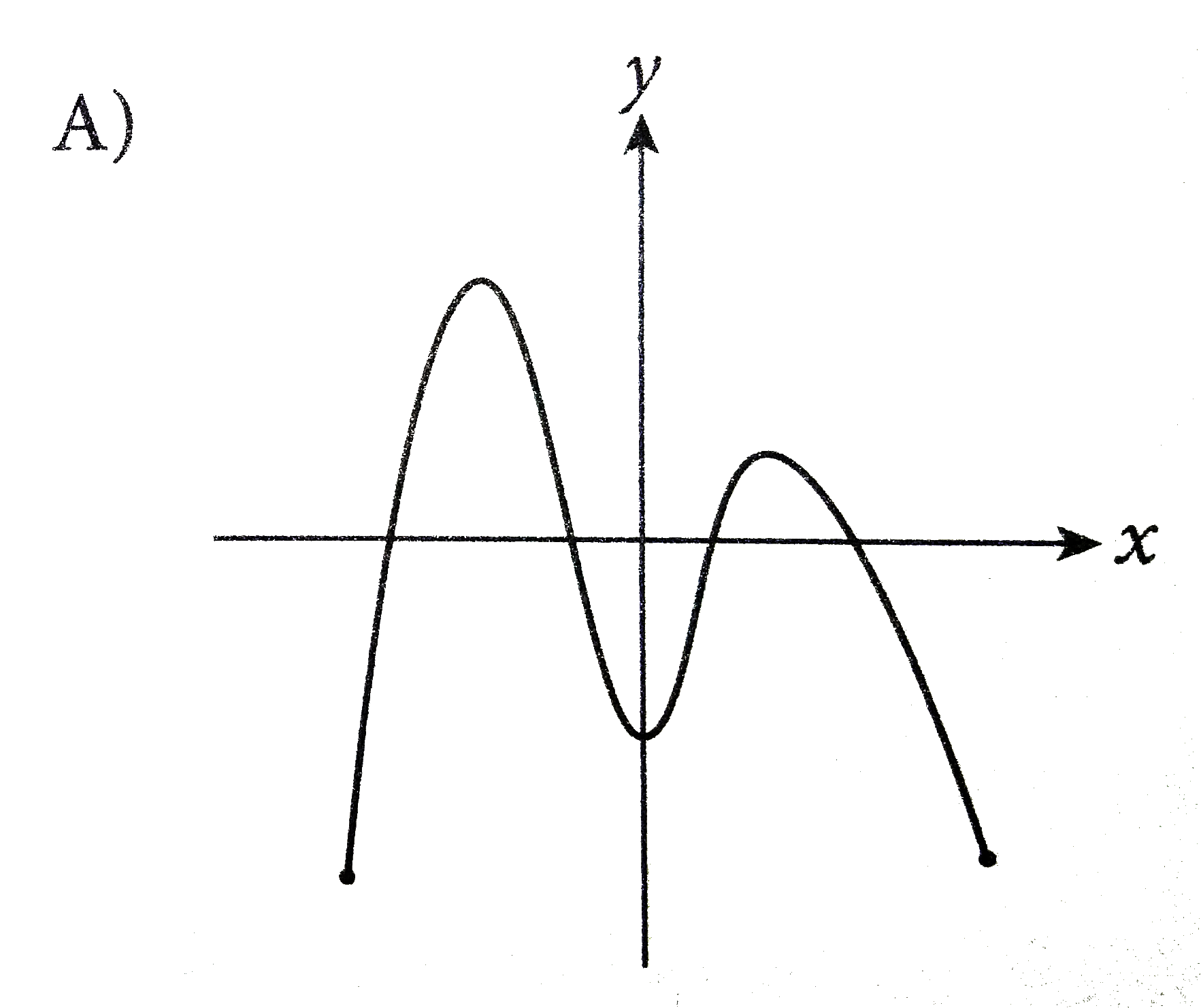 B
B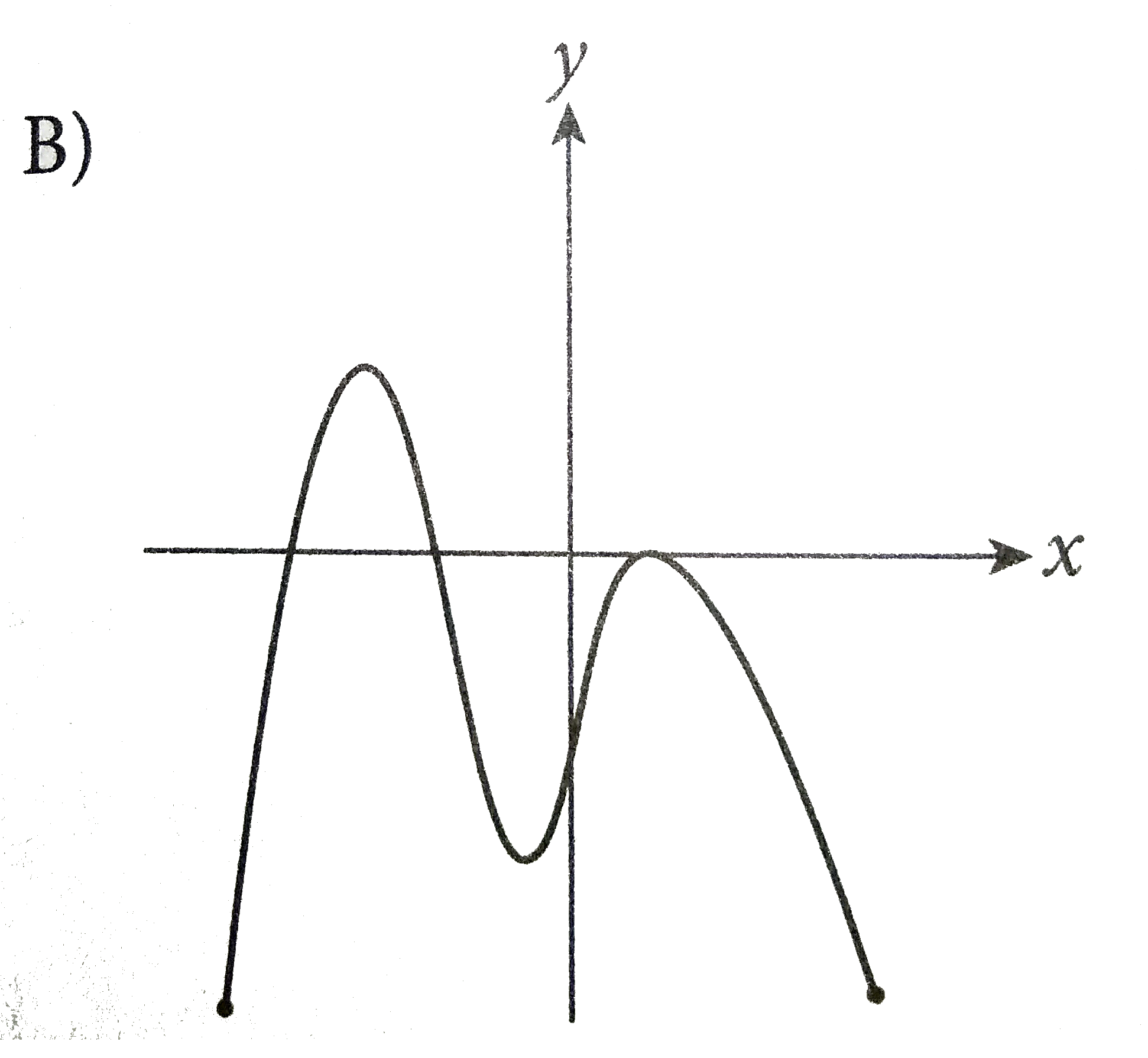 C
C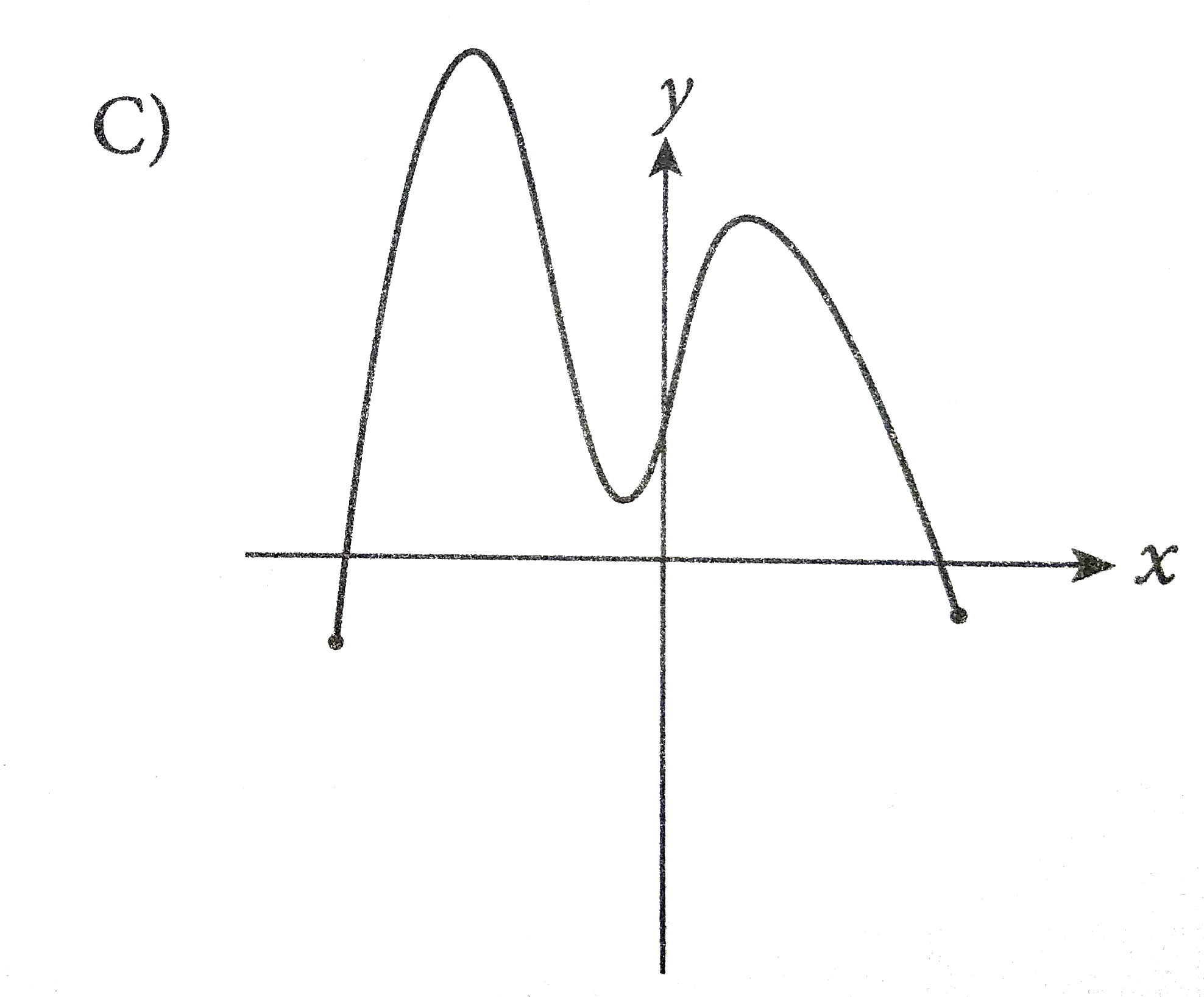 D
D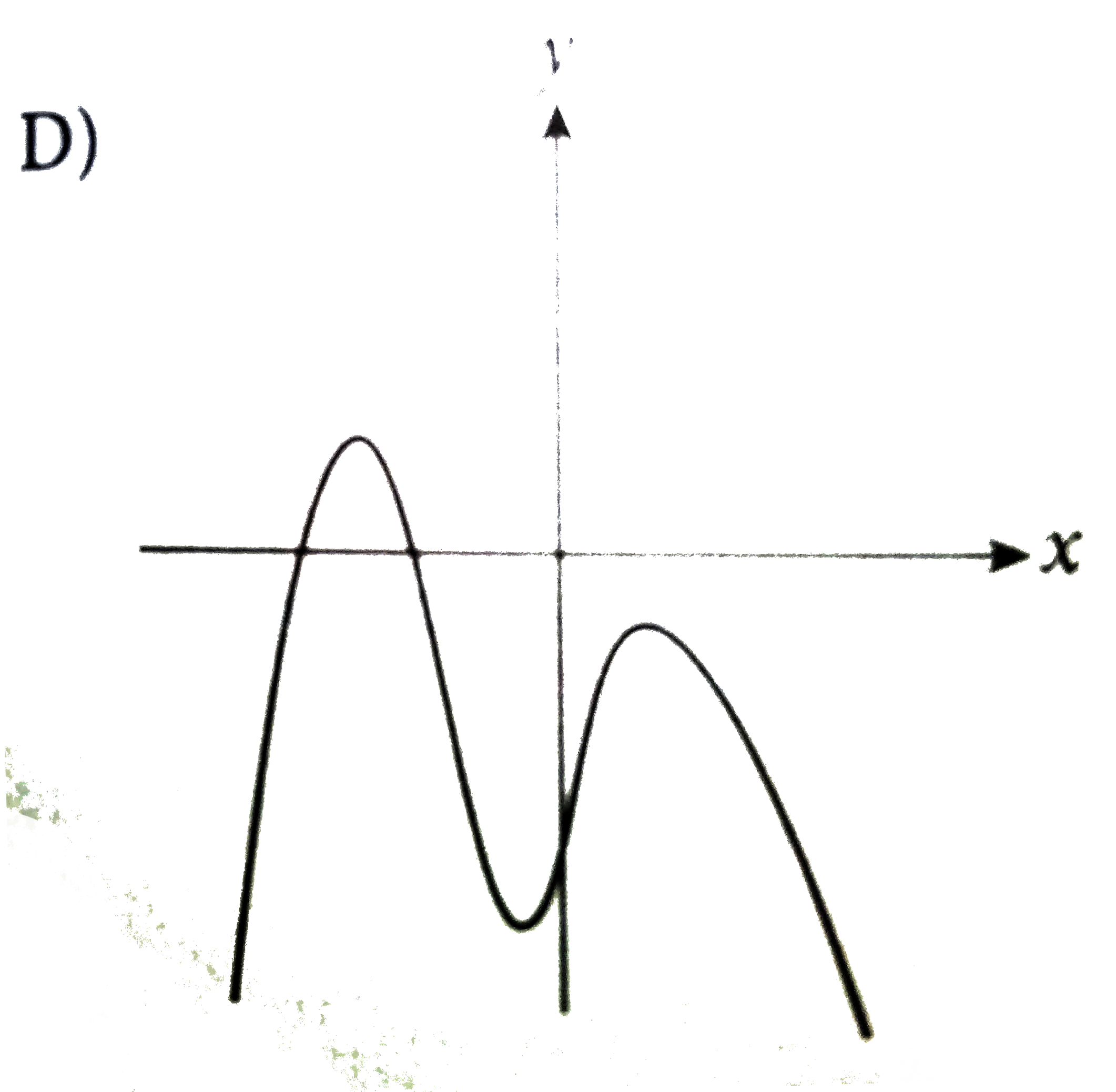
- Question 2 - Select One
12 If the function f has five distinct zeros, which of the following could represent the complete graph of f in the xy‑plane?
A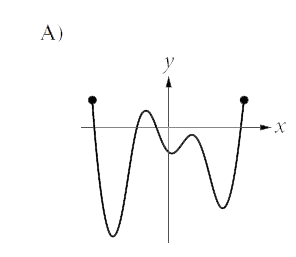 B
B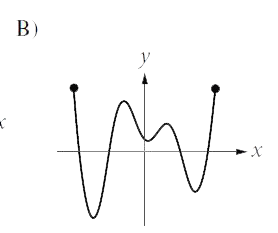 C
C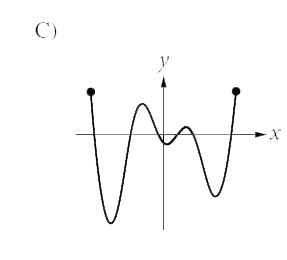 D
D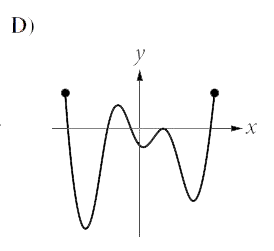
- Question 3 - Select One
Which of the following is the equation of a circle in the standard (x,y) coordinate plane ?
A(x-3)+(y+6)=100By=x2+25Cx2=y2+25Dx2=36−y2
If function f has exactly two distinct real zeros, which of the following graphs could be the complete graph of f (x) ?
View SolutionWhich of the following P-V diagram represent the graph of isometric process?
View Solution
The graph of the function f is shown above. Which of the following could represent the graph of y=|f(x)|?View Solutionf (x) = (x + 3)(x − k)
T he function f is defined above. If k is a positive integer, which of the following could represent the graph of y = f (x) in the xy-plane?View Solution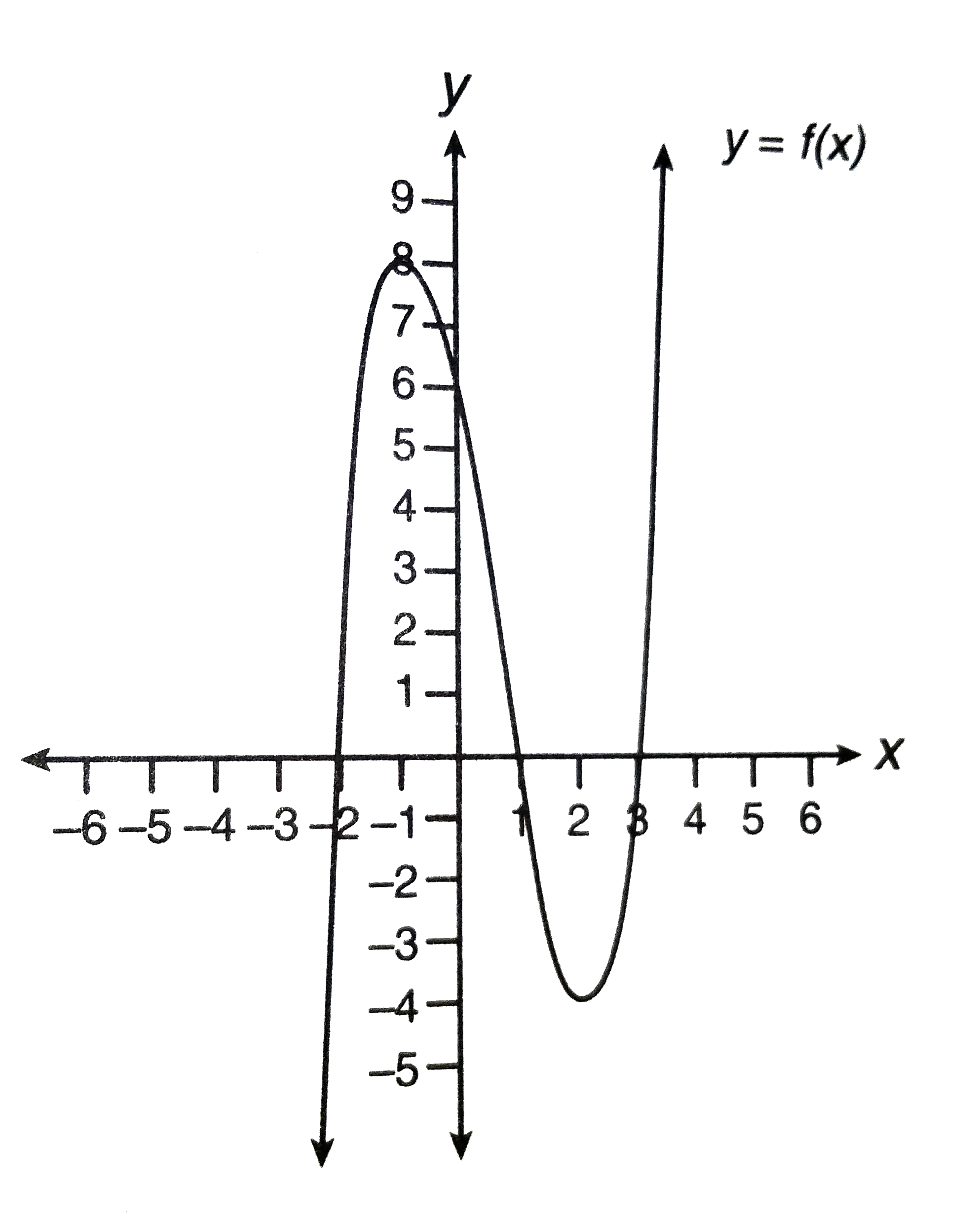
Which function could represents the graph above?View Solution