A square is inscribed in a circle of radius R, a circle is inscribed in this square then a square in this circle and so on n times. Find the limit of the sum of areas of all the squares as n→∞.
The correct Answer is:=4R2
To solve the problem step by step, we will analyze the geometric relationships between the squares and circles, and then calculate the limit of the sum of the areas of the squares as n approaches infinity.
Step 1: Determine the side length of the first square
Given a circle with radius R, the diameter of the circle is 2R. The diagonal of the inscribed square is equal to the diameter of the circle.
The diagonal d of a square with side length a is given by:
d=a√2
Setting the diagonal equal to the diameter of the circle, we have:
a√2=2R
Solving for a:
a=2R√2=R√2
Step 2: Determine the side length of subsequent squares
The second square is inscribed in the circle that is inscribed in the first square. The side length of the second square is half that of the first square:
a2=a1√2=R√2√2=R
Continuing this pattern, the side lengths of the squares can be expressed as:
- First square: a1=R√2
- Second square: a2=R
- Third square: a3=R√2
- Fourth square: a4=R2
- And so on...
In general, the side length of the n-th square can be expressed as:
an=R√2(√2)n−1=R2(n−1)/22(n−1)/2=R12(n−1)/2
Step 3: Calculate the area of each square
The area An of the n-th square is given by:
An=a2n=(R12(n−1)/2)2=R212n−1=R22n−1
Step 4: Sum the areas of all squares
The total area Sn of the first n squares is:
Sn=A1+A2+A3+…+An=R2(1+12+14+…+12n−1)
This series is a geometric series with the first term 1 and common ratio 12. The sum of the first n terms of a geometric series is given by:
Sn=a(1−rn)1−r
where a is the first term and r is the common ratio. Thus:
Sn=R2⋅1(1−(1/2)n)1−1/2=R2⋅1−(1/2)n1/2=2R2(1−(1/2)n)
Step 5: Find the limit as n→∞
As n approaches infinity, (1/2)n approaches 0. Therefore:
limn→∞Sn=2R2(1−0)=2R2⋅2=4R2
Final Result
The limit of the sum of the areas of all the squares as n approaches infinity is:
4R2
Given a circle with radius R, the diameter of the circle is 2R. The diagonal of the inscribed square is equal to the diameter of the circle.
d=a√2
Setting the diagonal equal to the diameter of the circle, we have:
a√2=2R
Solving for a:
a=2R√2=R√2
The second square is inscribed in the circle that is inscribed in the first square. The side length of the second square is half that of the first square:
a2=a1√2=R√2√2=R
- First square: a1=R√2
- Second square: a2=R
- Third square: a3=R√2
- Fourth square: a4=R2
- And so on...
an=R√2(√2)n−1=R2(n−1)/22(n−1)/2=R12(n−1)/2
The area An of the n-th square is given by:
An=a2n=(R12(n−1)/2)2=R212n−1=R22n−1
The total area Sn of the first n squares is:
Sn=A1+A2+A3+…+An=R2(1+12+14+…+12n−1)
Sn=a(1−rn)1−r
where a is the first term and r is the common ratio. Thus:
Sn=R2⋅1(1−(1/2)n)1−1/2=R2⋅1−(1/2)n1/2=2R2(1−(1/2)n)
As n approaches infinity, (1/2)n approaches 0. Therefore:
limn→∞Sn=2R2(1−0)=2R2⋅2=4R2
The limit of the sum of the areas of all the squares as n approaches infinity is:
4R2
Topper's Solved these Questions
- LIMITSBOOK - ARIHANT MATHS ENGLISHCHAPTER - LIMITSEXERCISE - Exercise (Single Option Correct Type Questions)
39 Videos
- LIMITSBOOK - ARIHANT MATHS ENGLISHCHAPTER - LIMITSEXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
2 Videos
Similar Questions
Knowledge Check
A square is inscribed in a circle with area 9z. What is the area of the square?
A3√2B9√2C18D36A square is circunscribed about a circle of 7-foot radius, as shown below. What is the area of the square in square feet?
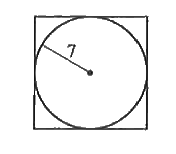 A49B56C98D196
A49B56C98D196
If a square of side 10 is inscribed in a circle then radius of the circle is
View SolutionIf a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
View SolutionIf a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
View SolutionA circle is inscribed in an equilateral triangle of side a. Find the area of any square inscribed in this circle.
View SolutionA circle is inscribed in a square of area 784cm2 Find the area of the circle.
View SolutionIf a circle is inscribed in a square of side 10, so that the circle touches the four sides of the square internally then radius of the circle is
View Solution
