A star constellation is approximately 3.1×104 light years from Earth. One light year is about 5.9×1012 miles. What is the approximately distance, in miles, between Earth and the constellation.
1.83×1017
9.0×1049
1.9×108
9.0×1016
The correct Answer is:A
To find the approximate distance in miles between Earth and the star constellation, we can follow these steps:
1. Identify the Given Values:
- Distance to the star constellation: 3.1×104 light years
- Distance of one light year in miles: 5.9×1012 miles
2. Set Up the Conversion:
- To find the distance in miles, we need to multiply the distance in light years by the distance of one light year in miles:
Distance in miles=Distance in light years×Distance of one light year in miles
Distance in miles=(3.1×104)×(5.9×1012)
3. Multiply the Coefficients:
- First, multiply the numerical coefficients:
3.1×5.9=18.29
4. Add the Exponents:
- Next, add the exponents of 10:
104×1012=10(4+12)=1016
5. Combine the Results:
- Now combine the results from steps 3 and 4:
Distance in miles=18.29×1016
6. Convert to Standard Scientific Notation:
- To express 18.29 in proper scientific notation, we can write it as:
1.829×101
- Therefore:
18.29×1016=1.829×101×1016=1.829×1017
7. Final Result:
- The approximate distance in miles between Earth and the constellation is:
Distance≈1.83×1017 miles
- Distance to the star constellation: 3.1×104 light years
- Distance of one light year in miles: 5.9×1012 miles
- To find the distance in miles, we need to multiply the distance in light years by the distance of one light year in miles:
Distance in miles=Distance in light years×Distance of one light year in miles
Distance in miles=(3.1×104)×(5.9×1012)
- First, multiply the numerical coefficients:
3.1×5.9=18.29
- Next, add the exponents of 10:
104×1012=10(4+12)=1016
- Now combine the results from steps 3 and 4:
Distance in miles=18.29×1016
- To express 18.29 in proper scientific notation, we can write it as:
1.829×101
- Therefore:
18.29×1016=1.829×101×1016=1.829×1017
- The approximate distance in miles between Earth and the constellation is:
Distance≈1.83×1017 miles
Topper's Solved these Questions
- PROBLEM SOLVING AND DATA ANALYSISBOOK - ENGLISH SATCHAPTER - PROBLEM SOLVING AND DATA ANALYSISEXERCISE - Grib-In
40 Videos
- PROBLEM SOLVING AND DATA ANALYSISBOOK - ENGLISH SATCHAPTER - PROBLEM SOLVING AND DATA ANALYSISEXERCISE - Grib-In
40 Videos
- PROBLEM SOLVING AND DATA ANALYSISBOOK - ENGLISH SATCHAPTER - PROBLEM SOLVING AND DATA ANALYSISEXERCISE - EXERICSE
80 Videos
- PROBLEMS IN CONTEXT BOOK - ENGLISH SATCHAPTER - PROBLEMS IN CONTEXT EXERCISE - PRACTICE TEST
10 Videos
Similar Questions
The distance of a star from the earth is 8.33 light minutes.' What do you mean by this statement ? Express the distance in metre.
View SolutionThe time taken by Mars to revolve round the sun is 1.88 years. Find the ratio of average distance between mars and the sun to that between the earth and the sun.
View Solution
Knowledge Check
The time taken by light to travel from sun to earth is approximately
A8 light yearsB8 secondsC8 minutesD8 hoursA cargo ship is 4.2 miles from a lighthouse, and a fishing boat is 5.0 miles from the lighthouse, as shown below. The angle between the straight lines from the lighthouse to the 3 vessels is 5∘. The approximate distance in miles, from the cargo ship to the fishing boat is given by which of the following expressions?
(Note: The law of cosines states that for any triangle with vertices A, B and C adn the sides opposite those vertices with length a, b, and c, respectively. c2=a2+b2−2abcosC).
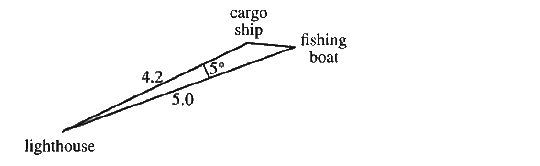 A√(5.0)2−(4.2)2B√(4.2)2+(5.0)2−2⋅4.2⋅5.0cos5∘C√(4.2)2+(5.0)2+2⋅4.2⋅5.0cos5∘D√(4.2)2+(5.0)2−2⋅4.2⋅5.0cos85∘
A√(5.0)2−(4.2)2B√(4.2)2+(5.0)2−2⋅4.2⋅5.0cos5∘C√(4.2)2+(5.0)2+2⋅4.2⋅5.0cos5∘D√(4.2)2+(5.0)2−2⋅4.2⋅5.0cos85∘The distnace of the moon from the earth is about 60 times the radius of the earth. What will be diameter of the earth (approximately in degrees) as see from the moon?
A1∘B2∘C4∘D6∘
Assertion : Light year and year, both measure time.
Reason : Because light year is the time light takes to reach the earth from the sun.
View SolutionAssertion : Light year and year, both measure time.
Reason : Because light year is the time light takes to reach the earth from the sun.
View SolutionIn a certain binary star system, each star has the same mass as our sun. They revolve about their centre of mass. The distance between them is the same as the distance between earth and the sun. What is their period of revolution in years ?
View SolutionA binary star has a time period 3 years (time period of earth is one year) while distance between the two stars is 9 times distance between earth and the sun. Mass of one star is equal to mass of the sun and mass of other is 20n times mass of the sun then calculate n.
View SolutionAn object detected or radar is 5 miles to the east, 4 miles to the north, and 1 mile above the tracking station. Among the following, which is the closet approximation to the distance, in miles, that the object is from the tracking station?
View Solution
