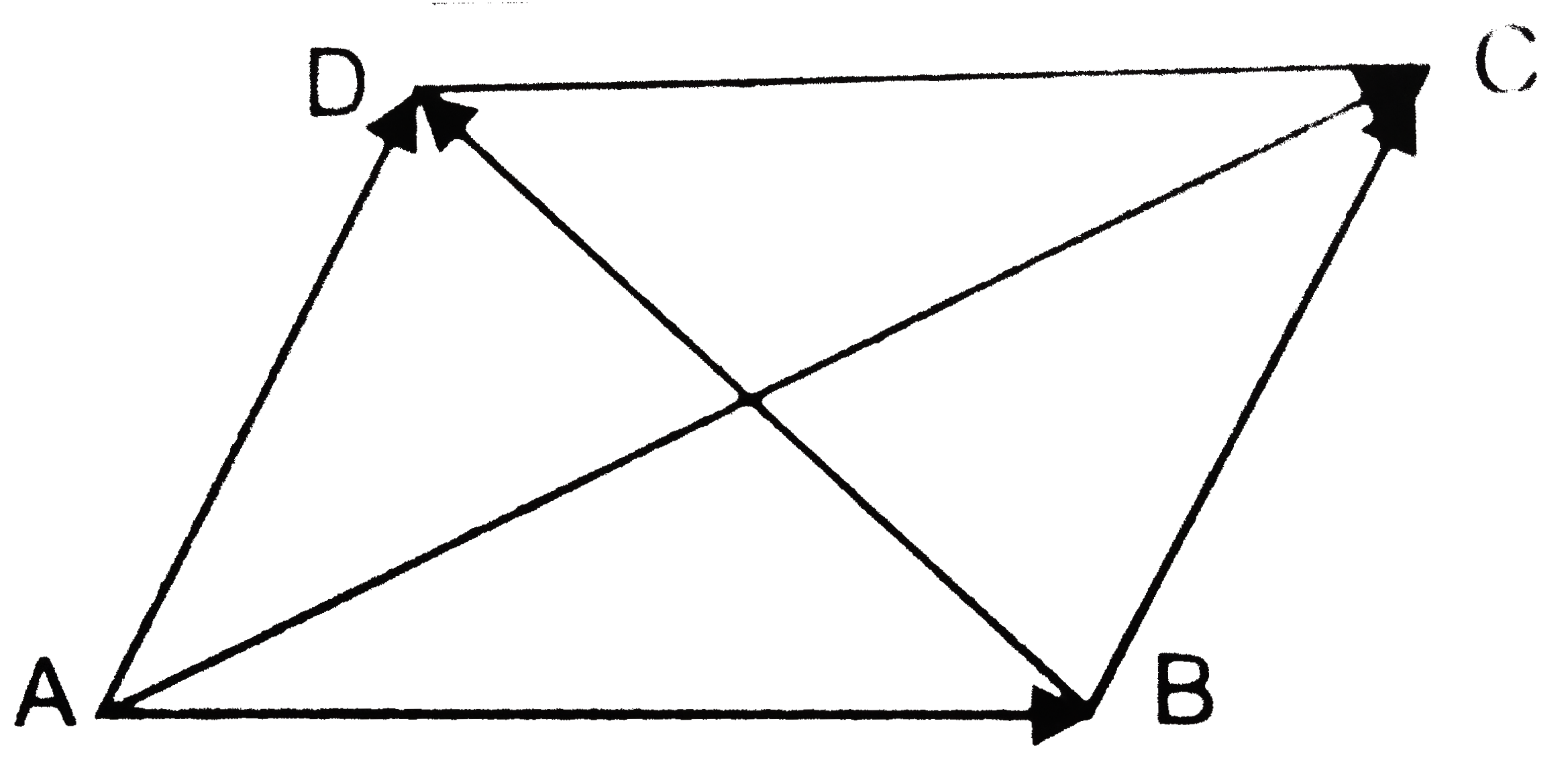
A straight line L cuts the sides AB, AC, AD of a parallelogram ABCD at B1,C1,d1 respectively. If −−→AB1=λ1−−→AB,−−−→AD1=λ2−−→ADand−−→AC1=λ3−−→AC, then 1λ3 equal to
λ1,λ3andλ2 are in AP
λ1,λ3andλ2 are in GP
λ1,λ3andλ2 are in HP
λ1+λ2+λ3=0
The correct Answer is:C
Step by step video, text & image solution for A straight line L cuts the sides AB, AC, AD of a parallelogram ABCD at B_(1), C_(1), d_(1) respectively. If vec(AB_(1))=lambda_(1)vec(AB), vec(AD_(1))=lambda_(2)vec(AD) and vec(AC_(1))=lambda_(3)vec(AC), then (1)/(lambda_(3)) equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - VK JAISWALCHAPTER - VECTOR & 3DIMENSIONAL GEOMETRYEXERCISE - Exercise-2 : One or More than One Answer is/are Correct21videos
VECTOR & 3DIMENSIONAL GEOMETRY
- BOOK - VK JAISWALCHAPTER - VECTOR & 3DIMENSIONAL GEOMETRYEXERCISE - Exercise-3 : Comprehension Type Problems18videos
VECTOR & 3DIMENSIONAL GEOMETRY
- BOOK - VK JAISWALCHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - Exercise-5 : Subjective Type Problems9videos
TRIGONOMETRIC EQUATIONS
Similar Questions
A straight line L cuts the lines AB,ACandAD of a parallelogram ABCD at points B1,C1andD1, respectively. If (→AB)1,λ1→AB,(→AD)1=λ2→ADand(→AC)1=λ3→AC, then prove that 1λ3=1λ1+1λ2 .
View SolutionLet B1,C1andD1 are points on AB,ACandAD of the parallelogram ABCD, such that −−→AB1=k1−−−→AC,−−→AC1=k2−−→ACand−−−→AD1=k2−−−→AD, where k1,k2andk3 are scalar.
View Solution
Knowledge Check
- Question 1 - Select One
ABCD a parallelogram, and A1andB1 are the midpoints of sides BC and CD, respectively. If −→aA1 +−−→AB1=λ−−→AC, then λ is equal to
A12B1C32D2 - Question 2 - Select One
E and F are the interior points on the sides BC and CD of a parallelogram ABCD. Let −−→BE=4−−→ECand−−→CF=4−−→FD. If the line EF meets the diagonal AC in G, then −−→AG=λ−−→AC, where λ is equal to :
A13B2125C713D215 - Question 3 - Select One
E and F are the interior points on the sides BC and CD of a parallelogram ABCD. Let −−→BE=4−−→ECand−−→CF=4−−→FD. If the line EF meets the diagonal AC in G, then −−→AG=λ−−→AC, where λ is equal to :
A13B2125C713D215
ABCD is a parallelogram and AC, BD are its diagonals. Show that :
−−→AC+−−→BD=2−−→BC,−−→AC−−−→BD=2−−→AB.View SolutionABCD is a parallelogram Fig. 2 (c ) .64. ACand(BD)areitsdiagonals.Showtˆ<br> (a) vec (AC) +vec (BD) =2 vec (BC)<br>(b)vec (AC) - vec (BD) =2 vec (AB)
 . View Solution
. View SolutionIf D,E and F are the mid-points of the sides BC, CA and AB respectively of a triangle ABC and λ is scalar, such that −−→AD+23−−→BE+13−−→CF=λ−−→AC, then λ is equal to
View SolutionABCD is a parallelogram with AC and BD as diagonals. Then, A→C−B→D=
View SolutionThe points A, B and C with position vectors →a,→band→c respectively lie on a circle centered at origin O. Let G and E be the centroid of ΔABCandΔACD respectively where D is mid point of AB.
Q. If [−−→AB−−→AC−−→AB×−−→AC]=λ[−−→AE−−→AG−−→AE×−−→AG], then the value of λ is :View Solution

