A tank initially contains 50 gallons of fresh water. Brine contains 2 pounds per gallon of salt, flows into the tank at the rate of 2 gallons per minutes and the mixture kept uniform by stirring, runs out at the same rate. If it will take for the quantity of salt in the tank to increase from 40 to 80 pounds (in seconds) is 206λ, then find λSolution in Punjabi
The correct Answer is:8
Step by step video & image solution for A tank initially contains 50 gallons of fresh water. Brine contains 2 pounds per gallon of salt, flows into the tank at the rate of 2 gallons per minutes and the mixture kept uniform by stirring, runs out at the same rate. If it will take for the quantity of salt in the tank to increase from 40 to 80 pounds (in seconds) is 206lambda, then find lambda by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL EQUATION Book:ARIHANT MATHSChapter:DIFFERENTIAL EQUATION Exercise:Exercise (Subjective Type Questions)
Explore 4 Videos
- DIFFERENTIAL EQUATION Book:ARIHANT MATHSChapter:DIFFERENTIAL EQUATION Exercise:Differential Equations Exerise 7 :
Explore 1 Video
- DIFFERENTIAL EQUATION Book:ARIHANT MATHSChapter:DIFFERENTIAL EQUATION Exercise:Differential Equations Exerise 5 :
Explore 3 Videos
- DETERMINANTS Book:ARIHANT MATHSChapter:DETERMINANTS Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 18 Videos
- DIFFERENTIATION Book:ARIHANT MATHSChapter:DIFFERENTIATION Exercise:Exercise For Session 10
Explore 4 Videos
Similar Questions
A hemi-spherical tank of radius 2 m is initially full of water and has an outlet of 12cm2 cross-sectional area at the bottom. The outlet is opened at some instant. The flow through the outlet is according to the law v(t)=0.6√2gh(t), where v(t) and h(t) are, respectively, the velocity of the flow through the outlet and the height of water level above the outlet and the height of water level above the outlet at time t, and g is the acceleration due to gravity. Find the time it takes to empty the tank.
View SolutionLet y=f(x) be a differentiable function ∀x∈R and satisfies:
f(x)=x+∫10x2zf(z)dz+∫10xz2f(z)dz.
View SolutionProve that 3tan2(π6)+cosesc(π6)+2tan2(π3)=9
View SolutionIf a2+b2+c2=−2, and f(x)= ∣∣ ∣ ∣∣1+a2x(1+b2)x(1+c2)x(1+a2)x1+b2x(1+c2)x(1+a2)x(1+b2)x1+c2x∣∣ ∣ ∣∣ , then f(x) is a polynomial of degree
View SolutionThe functions f(x)−ex+x, being differentiable and one-one, has a differentiable inverse f−1(x) The value of ddxf−1 at the point f(log2) is
View SolutionTwo pipes can fill a tank in 20 and 24 minutes respectively and a waste pipe can empty 3 gallons per minute. All the three pipes working together can fill the tank in 15 minutes. The capacity of the tank is 60 gallons b. 100 gallons c. 120 gallons d. 180 gallons
View SolutionA 50 L tank initailly contains 10 L of fresh water, At t=0, a brine solution containing 1 lb of salt per gallon is poured into the tank at the rate of 4 L/min, while the well-stirred mixture leaves the tank at the rate of 2 L/min. Then the amount of time required for overflow to occur in
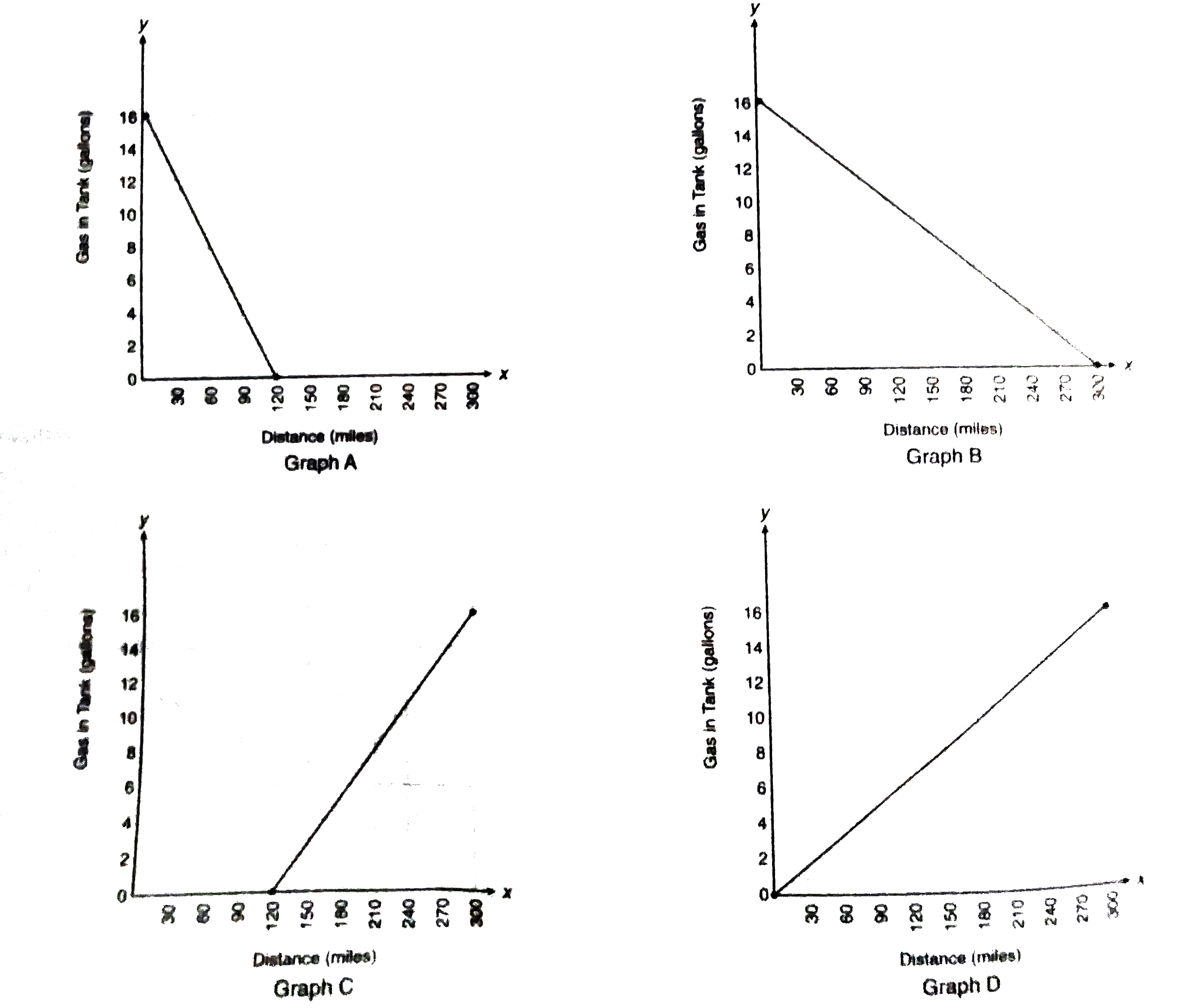
View SolutionThe gas tank in a car holds a total of 16 gallons of gas. The car travels 75 miles on 4 gallons of gas. If the gas tank is full at the beginning of a trip, which graph represents the rate of change in the amount of gas in the tank?
View SolutionA tank initially contains 50 litres of pure water. Starting at time t = 0 a brine containing with 2 grams of dissolved salt per litre flows into the tank at the rate of 3 litres per minutes. The mixture is kept uniform by stirring and the well - stirred mixture simultaneously flows out of the tank at the same rate. Find the amount of salt present in the tank at any time t>0.
View SolutionA partially filled pool contains 600 gallons of water. A hose is turned on, and water flows into the pool at the rate of 8 gallons per minute. How many gallons of water will be in the pool after 70 minutes?
View SolutionA tank consists of 50 litres of fresh water. Two litres of brine each litre containing 5 gms of dissolved salt are run into tank per minute, the mixture is kept uniform by stirring, and runs out at the rate of one litre per minute. If ‘m’ grams of salt are present in the tank after t minute, express ‘m’ in terms of t and find the amount of salt present after 10 minutes
View SolutionA tank contains 1000 litres of water in which 100 grams of salt is dissolved Salt solution runs at a rate 10 litres per minute , each litre contains 5 grams of dissolved salt . The mixture of the tank is kept uniform by stirring . Salt solution runs out at 20 litres per minute . Find the amount of salt at any time .
View SolutionA tank contains 1000 liters of water in which 100 grams of salts is dissolved brine runs in a rate of 10 liter per minute and each litre contains 5 grams of dissolved salt the mixture of the tank is kept uniform by stirring brine runs out at 10 liter per minute find the amount of salt at any time t
View Solutionஆரம்பத்தில் ஒரு தொட்டியில் 50 லிட்டர் தூய்மையான தண்ணீர் உள்ளது. தொடக்க நேரம் t=0-ல் ஒரு லிட்டர் நீரில் 2 கிராம் வீதம் கரைக்கப்பட்ட உப்புக் கரைசலானது ஒரு நிமிடத்திற்கு 3 லிட்டர் வீதம் தொட்டியில் விடப்படுகிறது. இக்கலவையானது தொடர்ந்து கலக்கப்பட்டு சீராக வைக்கப்படுகிறது. மேலும், அதே நேரத்தில் நன்கு கலக்கப்பட்ட இக்கலவையானது அதே வீதத்தில் தொட்டியிலிருந்து வெளியேறுகிறது. t=0 எனும் ஏதேனும் ஒரு நேரத்தில் தொட்டியில் உள்ள உப்பின் அளவினைக் காண்க.
View SolutionA 50 L tank initailly contains 10 L of fresh water, At t=0, a brine solution containing 1 lb of salt per gallon is poured into the tank at the rate of 4 L/min, while the well-stirred mixture leaves the tank at the rate of 2 L/min. Then the amount of time required for overflow to occur in
View Solutionएक टैंक में 5000L पानी में 20kg नमक घुला हुआ है। टैंक में प्रति मिनट 25L ब्राइन जिसकी सांद्रता 0.03 किग्रा प्रति लीटर है, डाली जा रही है। यदि मिश्रण समांग है तथा समान दर से बाहर निकाला जा रहा है, तों में 30 मिनट बाद कितना नमक रहेगा?
View Solution
