A hemi-spherical tank of radius 2 m is initially full of water and has an outlet of 12cm2 cross-sectional area at the bottom. The outlet is opened at some instant. The flow through the outlet is according to the law v(t)=0.6√2gh(t), where v(t) and h(t) are, respectively, the velocity of the flow through the outlet and the height of water level above the outlet and the height of water level above the outlet at time t, and g is the acceleration due to gravity. Find the time it takes to empty the tank.Solution in Punjabi
The correct Answer is:t=7×105135√g
Step by step video & image solution for A hemi-spherical tank of radius 2 m is initially full of water and has an outlet of 12c m^2 cross-sectional area at the bottom. The outlet is opened at some instant. The flow through the outlet is according to the law v(t)=0.6sqrt(2gh(t)), where v(t) and h(t) are, respectively, the velocity of the flow through the outlet and the height of water level above the outlet and the height of water level above the outlet at time t , and g is the acceleration due to gravity. Find the time it takes to empty the tank. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHSCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Differential Equations Exerise 7 :
1 Videos
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHSCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
26 Videos
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHSCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise (Single Integer Answer Type Questions)
8 Videos
- DETERMINANTS BOOK - ARIHANT MATHSCHAPTER - DETERMINANTS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
- DIFFERENTIATION BOOK - ARIHANT MATHSCHAPTER - DIFFERENTIATION EXERCISE - Exercise For Session 10
4 Videos
Similar Questions
Let y=f(x) be a differentiable function ∀x∈R and satisfies:
f(x)=x+∫10x2zf(z)dz+∫10xz2f(z)dz.
View SolutionIf f:R−{−1}→Randf is differentiable function satisfies:
f((x)+f(y)+xf(y))=y+f(x)+yf(x)∀x,
y∈R−{_1} Find f(x).
View SolutionFind the constant of intergration by the general solution of the differential equation (2x2y−2y4)dx+(2x3+3xy3)dy=0 if curve passes through (1,1).
View SolutionIf a2+b2+c2=−2, and f(x)= ∣∣ ∣ ∣∣1+a2x(1+b2)x(1+c2)x(1+a2)x1+b2x(1+c2)x(1+a2)x(1+b2)x1+c2x∣∣ ∣ ∣∣ , then f(x) is a polynomial of degree
View SolutionThe functions f(x)−ex+x, being differentiable and one-one, has a differentiable inverse f−1(x) The value of ddxf−1 at the point f(log2) is
View SolutionFind the time required for a cylindrical tank of radius r and height H to empty through a round hole of area a at the bottom. The flow through the hole is according to the law v(t)=k√2gh(t) , where v(t) and h(t) , are respectively, the velocity of flow through the hole and the height of the water level above the hole at time t, and g is the acceleration due to gravity.
View SolutionWater filled in an empty tank of area 10 A through a tap of cross sectional area A. The speed of water flowing out of tap is given by v(m/s) =10(1-sin((pi)/(30)t) where t is in second. The height of water level from the bottom of the tank at t=15 second will be:
View Solution2 मीटर त्रिज्या का एक अंगोलाकार टैंक पानी से पूर्ण भरा हुआ है। जिसके तल भाग में 2 वर्ग सेमी अनुप्रस्थ काट वाली एक टोंटी लगी है। टोंटी को कुछ समय के लिए खोल दिया जाता है। टोंटी से निकलने वाले पानी का रिसाव V(t)=0.6√2gh(t) नियम के अनुसार है, जहाँV(t) तथा h(t) समय t पर क्रमशः टोंटी से निकलने वाले पानी का वेग तथा टोंटी से पानी के तल की ऊँचाई है तथा g गुरुत्वाकर्षण के कारण त्वरण है। टैंक के खाली होने में लगा समय ज्ञात कीजिए।
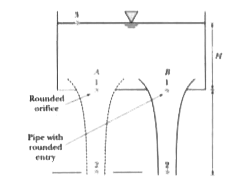
View SolutionA tank has two outlets (i) a rounded orifice A of diameter D and (ii) a pipe B with well - rounded entry and of length L , as shown in Fig. For a height of water H in the tank , determine the (a) discharge from the outlets A and B , (b) velocities in the two outlets at levels 1 and 2 indicated in Fig .
View SolutionThe intake in Figure, Reservoir has cross-sectional area of 0.740 m^(2) and water flows in at 0.400 m/s. At the outlet, the cross-sectional area is smaller than at the intake and the water flows out at 9.50 m/s. The pressure difference between intake and outlet is 3.00 MPa. What is vertical distance D?
View SolutionFind the time required for a cylindrical tank of radius r and height H to empty through a round hole of area a at the bottom. The flow through the hole is according to the law v(t)=k√2gh(t) , where v(t) and h(t) , are respectively, the velocity of flow through the hole and the height of the water level above the hole at time t, and g is the acceleration due to gravity.
View SolutionFind the time required for a cylindrical tank of radius r and height H to empty through a round hole of area a at the bottom. The flow through the hole is according to the law v(t)=k√2gh(t) , where v(t) and h(t) , are respectively, the velocity of flow through the hole and the height of the water level above the hole at time t, and g is the acceleration due to gravity.
View Solution2 मीटर त्रिज्या का एक अंगोलाकार टैंक पानी से पूर्ण भरा हुआ है। जिसके तल भाग में 2 वर्ग सेमी अनुप्रस्थ काट वाली एक टोंटी लगी है। टोंटी को कुछ समय के लिए खोल दिया जाता है। टोंटी से निकलने वाले पानी का रिसाव V(t)=0.6√2gh(t) नियम के अनुसार है, जहाँV(t) तथा h(t) समय t पर क्रमशः टोंटी से निकलने वाले पानी का वेग तथा टोंटी से पानी के तल की ऊँचाई है तथा g गुरुत्वाकर्षण के कारण त्वरण है। टैंक के खाली होने में लगा समय ज्ञात कीजिए।
View SolutionA tank has 8 pipes. Out of which some one inlet and some one outlets. Inlet pipe can fill a tank in 8 hours and an outlet pipe can empty the tank in 6 hours. If all pipes are opened together then the tank get filled in 8 hours. Find the number of inlets and outlets pipe.
View SolutionWhat will happen if the upper outlet of the condenser is connected to the tap instead of the lower outlet?
View SolutionWater filled in an empty tank of area 10 A through a tap of cross sectional area A. The speed of water flowing out of tap is given by v(m/s) =10(1-sin((pi)/(30)t) where t is in second. The height of water level from the bottom of the tank at t=15 second will be:
View Solution
