A toy company manufactures two types of dolls A and B. Market research and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is at most half of that for dolls of type A. Further the production level of dolls of type A can exceed three times the production of dolls of other type by at most 600 units. If the company makes profit of Rs. 12 and Rs. 16 per doll respectively on dolls A and B how many of each should be produced weekly in order to maximise the profit?

Text Solution

Verified by Experts

Let the company makes $x$ dolls of type A and $y$ dolls to type B.
$∴$ Maximise $Z = 12 x + 16 y$
$x \geq 0, y \geq 0$ ……………. 1
$x + y \leq 1200$ …………….2
$y \leq x / 2 \Rightarrow x - 2 y \geq 0$ ……………3
$x \leq 3 y + 600 \Rightarrow x - 3 y \leq 600$ ……………….4
First, draw the graph of the line $x + y = 1200$

Put $(0, 0)$ in the inequation $x + y \leq 1200$ ,
$0 + \leq 1000 \Rightarrow 0 \leq 1200$ (True)
Thus, the half plane contains the origin.
Now, draw the graph of the line $x - 2 y = 0$ .

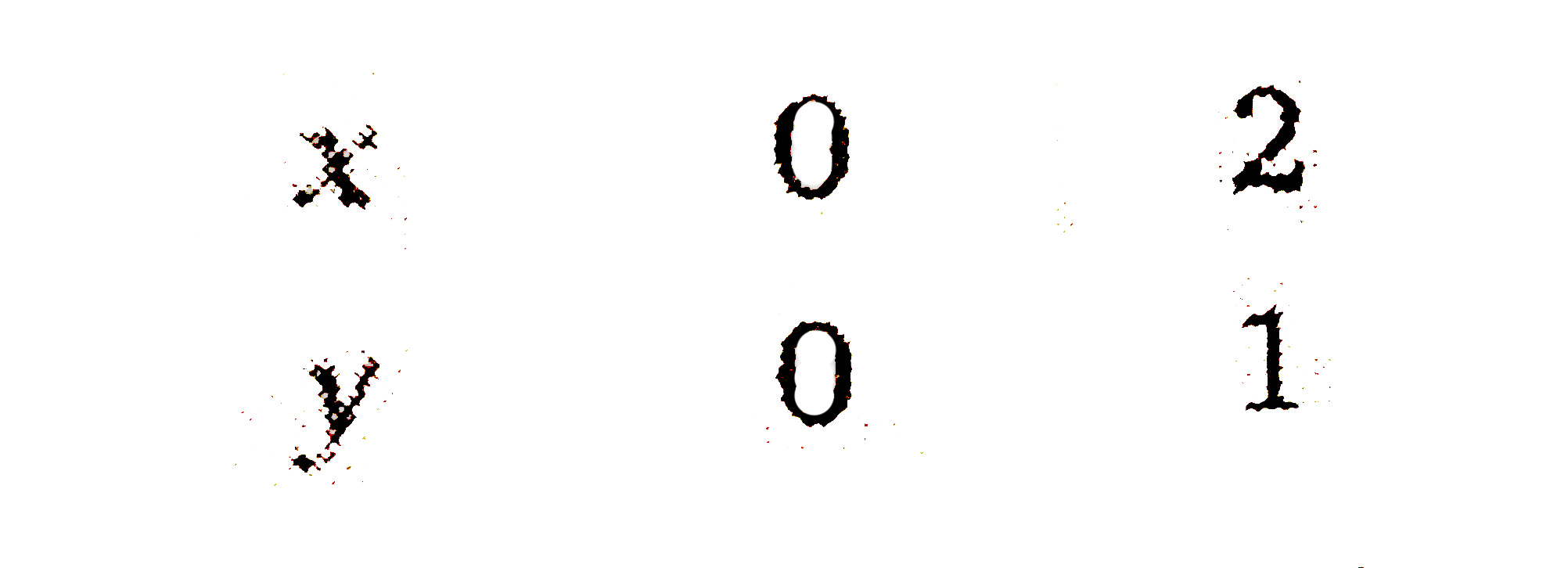
Put $(200, 0)$ in the ineuation $x - 2 y > 0$ ,
$2002 x 0 \geq 0 \Rightarrow 200 \geq 0$ (True)
Therefore, half plane is on the side of $x$ -axis.
Now, draw the graph of the line $x - 3 y = 600$ .

Put $(0, 0)$ in the inequation $x - 3 y \leq 600$
$0 + 3 \times 0 \leq 600 \Rightarrow 0 \leq 600$ (True)
Thus, the half plane contains the origin.
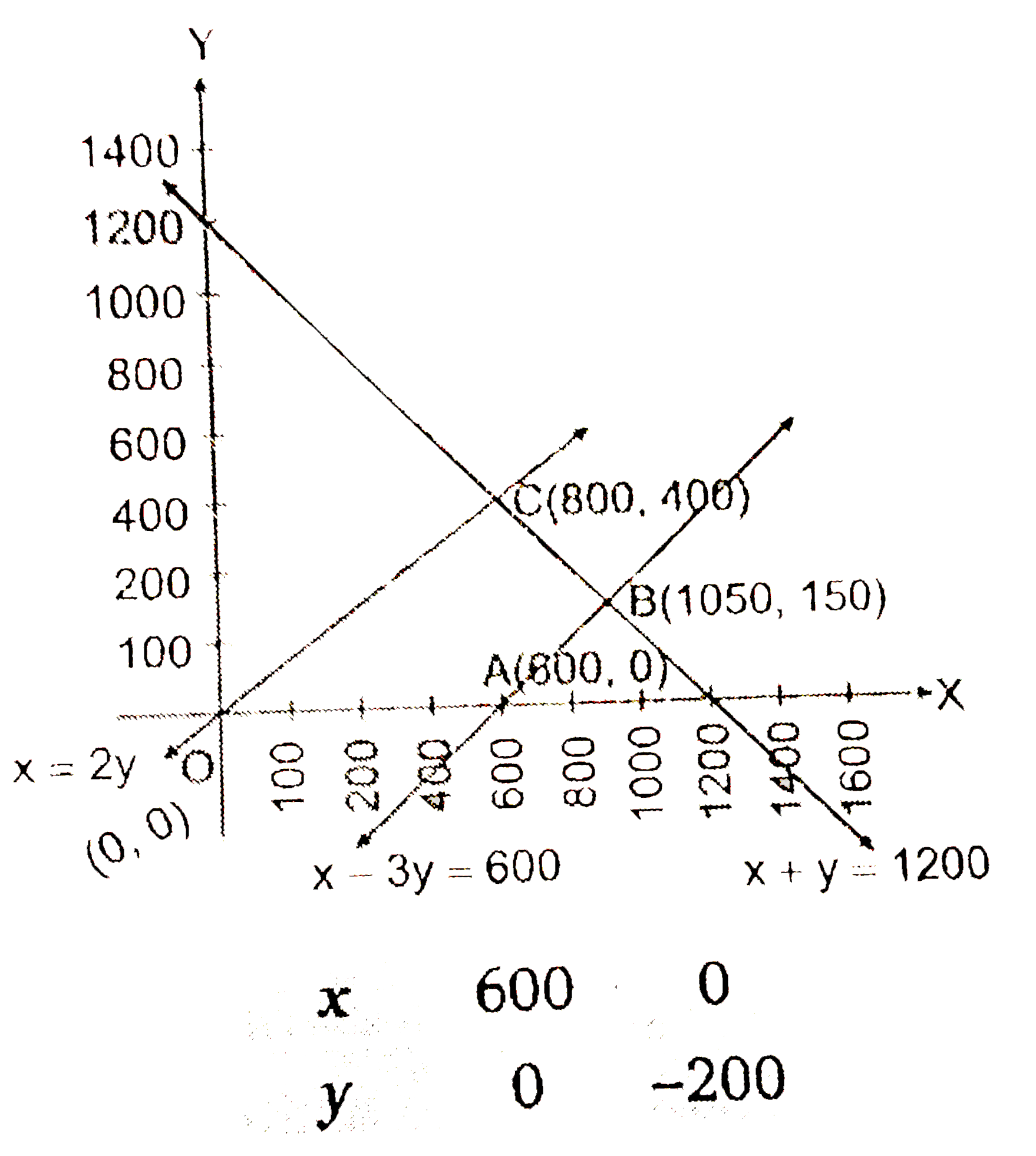
Since $x, y \geq 0$ . So, the feasible region is in first quadrant.
The point of intersection of the lines $x - 3 y = 600$ and $x + y = 1200$ is $B (1050, 150)$ and for the lines $x = 2 y$ and $x + y = 1200$ is $C (800, 400)$ .
$∴$ Feasible region is OABCO.
The vertices of the feasible region are $A (600, 0), B (1050, 150)$ and $C (800, 400)$ . We find the value of $Z$ at these vertices.

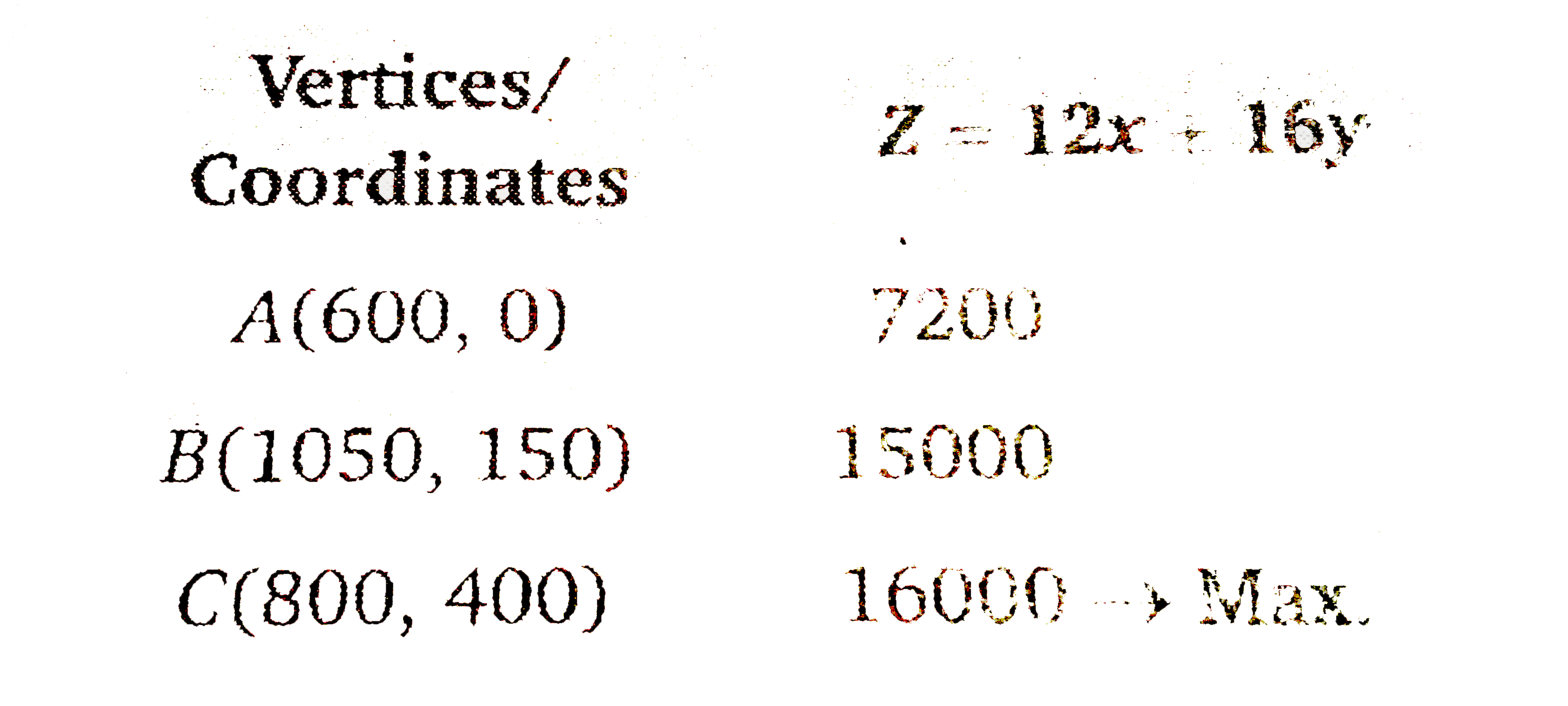
Maximum value of $Z$ is 16000 at $C (800, 400)$ .
Therefore, to obtain maximum profit of Rs. 16000, 800 dolls of type A and 400 dolls of type B should be produced.

|

Class 12 MATHS LINEAR PROGRAMMING

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-LINEAR PROGRAMMING-Miscellaneous Exercise

Home
Ask Doubt
Profile