A triangle ABC is inscribed in a circle. The bisector of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P,Q and R respectively . Prove that :
(i) ∠ABC=2∠APQ.
(ii) ∠ACB=2∠APR.
(iii) ∠QPR=90∘−12∠BAC.

Step by step video & image solution for A triangle ABC is inscribed in a circle. The bisector of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P,Q and R respectively . Prove that : (i) angle ABC = 2 angle APQ . (ii) angle ACB = 2 angle APR . (iii) angle QPR = 90 ^(@) -(1)/(2) angle BAC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(B)
10 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )
28 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )
28 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (PROBABILITY)
16 Videos
- CONSTRUCTIONS (CIRCLES)BOOK - ICSECHAPTER - CONSTRUCTIONS (CIRCLES)EXERCISE - EXERCISE
39 Videos
Similar Questions
Bisectors of vertex angles A, B and C of a triangle ABC intersect its circumcircle at the points D,E and F respectively. Prove that angle EDF=90∘−12∠A
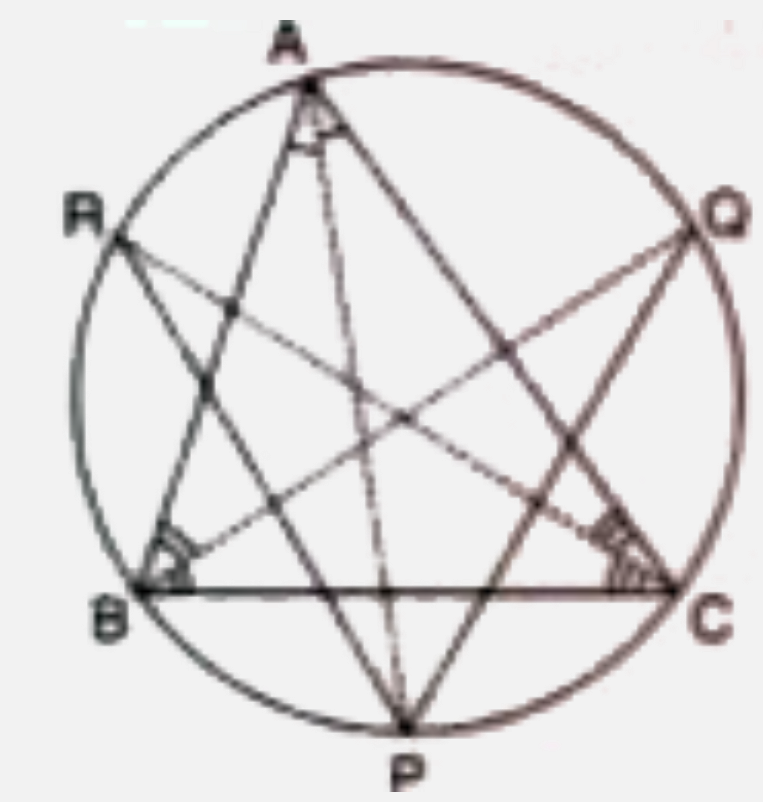
View SolutionThe given figure shows a triangle ABC with ∠BAC=56∘and∠ABC=64∘, Bisectors of angles A,B and C meet the circumcircle of the ΔABC at points P,Q and R respectively . Find the measure of ∠QPR.
View SolutionThe bisectors of angles A and B of a scalene triangle ABC meet at O.
What is the point O called ?
View SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ACB=72∘, calculate:
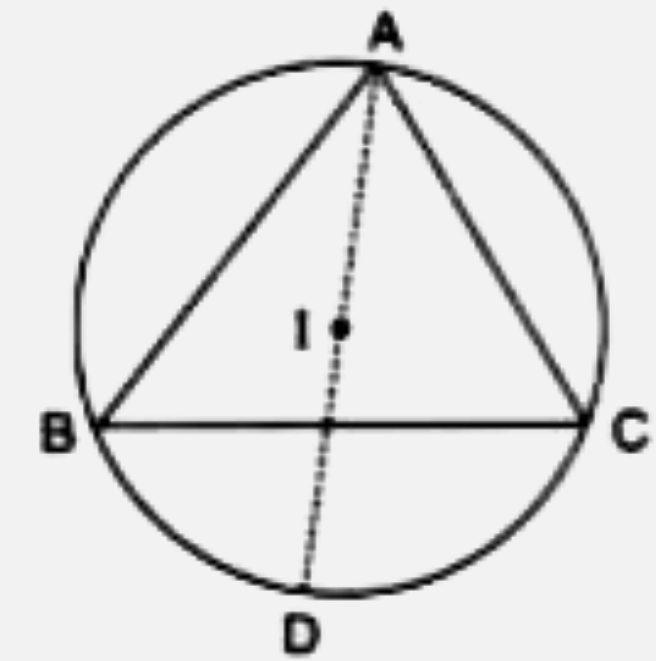
∠BCD
View SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ACB=72∘, calculate:

∠CBD
View SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ABC=72∘, calculate:

∠DCI
View SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ABC=72∘, calculate:

∠BIC
View SolutionThe circumcentre of the triangle ABC is O . Prove that ∠OBC+∠BAC=90∘.
View SolutionTriangle ABC is right angles at B. Internet bisectors of acute angles A and C meet at point I. Find the measure of angle AIC
View SolutionBisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90∘−12A,90∘−12B and 90∘−12C
View Solution
