In the given figures , the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB=75∘and∠BCD=40∘ find :
(i) ∠AOB
(ii) ∠ACB.
(iii) ∠ABD.
(iv) ∠ADB.

The correct Answer is:(i)150∘(ii)30∘(iii)110∘(iv)30∘
Step by step video & image solution for In the given figures , the centre O of the small circle lies on the circumference of the bigger circle. If angle APB = 75^(@) and angle BCD = 40 ^(@) find : (i) angle AOB (ii) angle ACB . (iii) angle ABD . (iv) angle ADB . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(B)
10 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )
28 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )
28 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (PROBABILITY)
16 Videos
- CONSTRUCTIONS (CIRCLES)BOOK - ICSECHAPTER - CONSTRUCTIONS (CIRCLES)EXERCISE - EXERCISE
39 Videos
Similar Questions
In the given figure, find ∠AOB.

View SolutionIn the given figure,AB is parallel to DC. ∠BCE=80∘and∠BAC=25∘.F∈d:(i) angle CAD <br>(ii) angle CBD <br>(iii) angle ADC
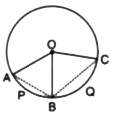
View SolutionIn the given figure , arc APB : arc BQC = 2: 3 and ∠AOC=150∘, Find :
(i) ∠AOB
(ii) ∠BOC
(iii) ∠OBA
(iv) ∠OCB
(v) ∠ABC
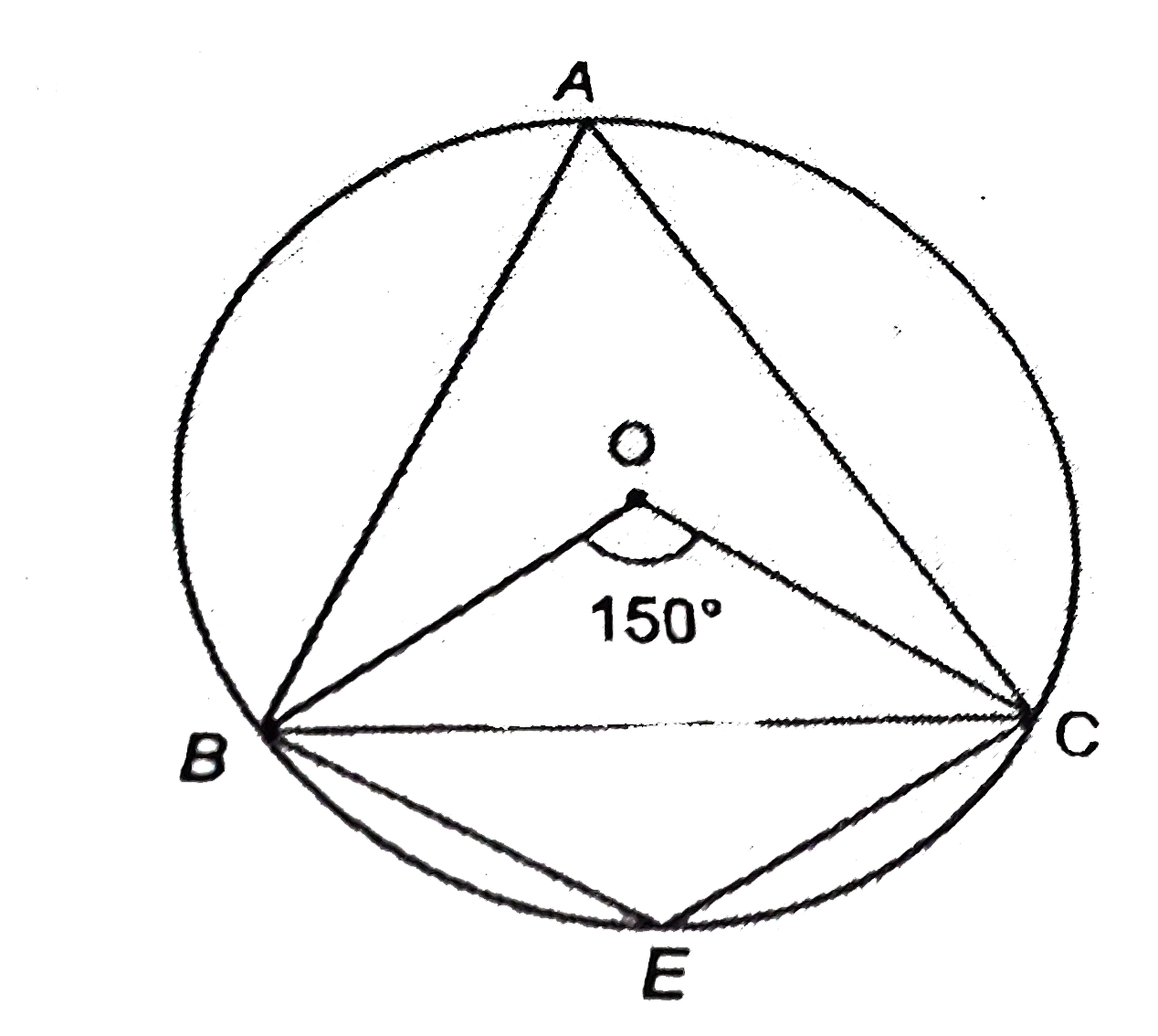
View SolutionIn the adjoining figure, O is the centre of the circle. Find the value of ∠BEC.
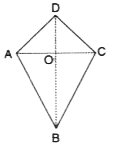
View SolutionThe given figures shows a kite- shaped figure whose diagonals intersect each other at point O. if
∠ABO=25∘and∠OCD=40∘, Find
(i) ∠ABC
(ii) ∠ADC
(iii) ∠BAD
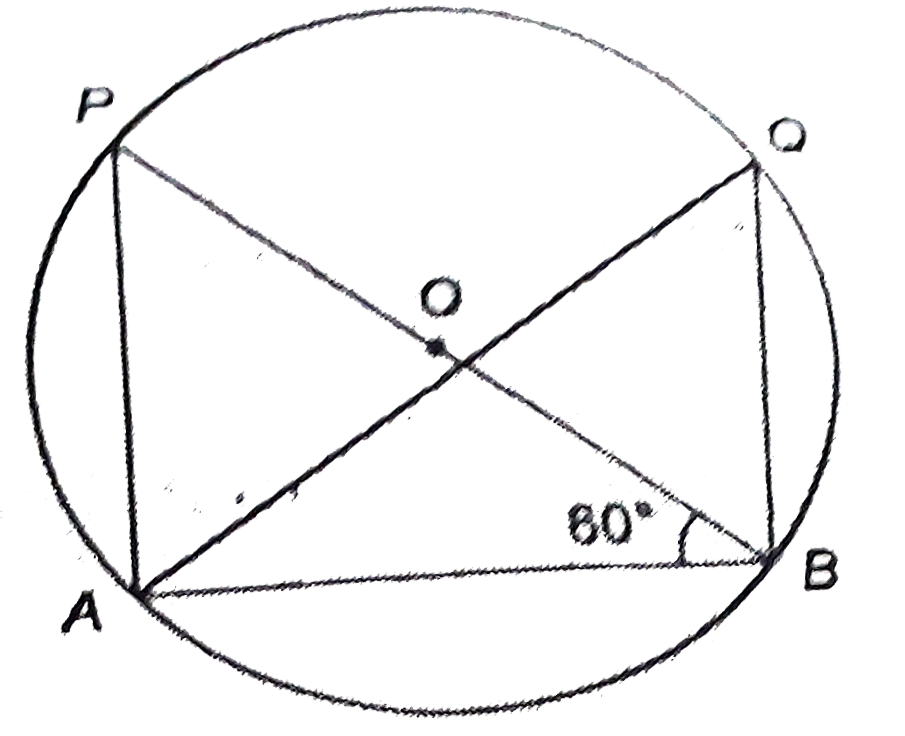
View SolutionIn the adjoining figure, BP is the diameter of the circle. If ∠ABP=60∘, then find ∠AQB.
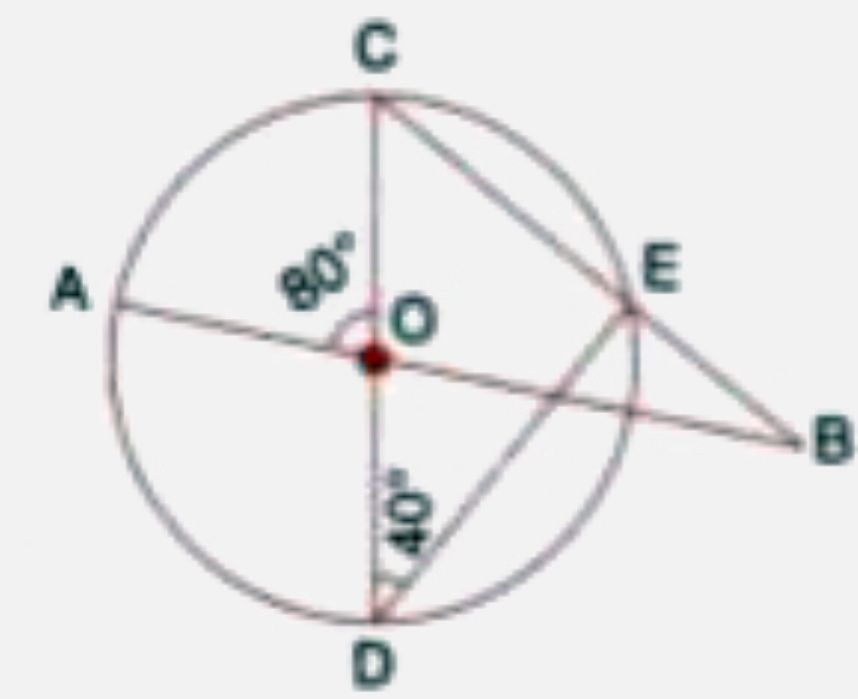
View SolutionIn the figure given alongside ,AB and CD are straight lines thorugh the centre O of a circle. If ∠AOC=80∘and∠CDE=40∘ , find ∠DCE
View SolutionIn the adjoining figure, O is the centre of the circle. If ∠AOB=150∘ and ∠BOC=100∘, then find the value of ∠ABC.

View SolutionIn the given figure , AD is a diameter O is the centre of the circle AD is parallel to BC and ∠CBD=32∘
(i) ∠OBD
(ii )∠AOB
(iii) ∠BED

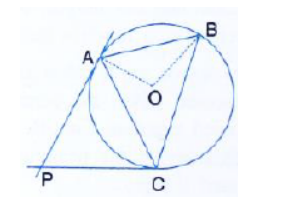
View SolutionIn the given figure, O is the centre of the circumcircle of △ABC. Tangents at A and C intersect at P. Given angle AOB=140∘ and angle APC=80∘ find the angle BAC.
View Solution
