A vertex of common graph of inequalities 2x+y≥2 and x−y≤3 , is
A
(0,0)
B
(53,−43)
C
(53,43)
D
(−43,53)
Video Solution
Text Solution
The correct Answer is:B
To find a common vertex of inequalities 2x+y≥2andx−y≤3, solve the following equations
2x+y=2.......(i)
and x−y=3...(ii)
On solving Eqs. (i) and (ii) , we get
x=53andy=−43 .
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The vertex of common graph of inequalities 2x+y≥2andx−y≤3 , is
A(0,0)B(53,−43)C(53,43)D(−43,53) - Question 2 - Select One
The graph of inequality 3x+y≤3 is:
Aclosed half plane that contains the origin.Bopen half plane that contains the origin.Copen half plane not containing the origin.Dclosed half plane not containing the origin. - Question 3 - Select One
The solution set of the inequalities 2x+y≥4,x+y≤x,2x−3y≤6 is
A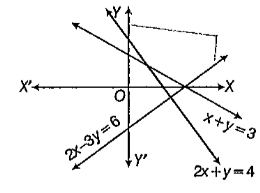 B
B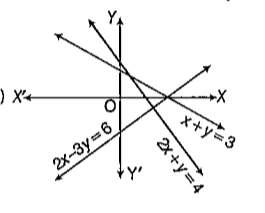 C
C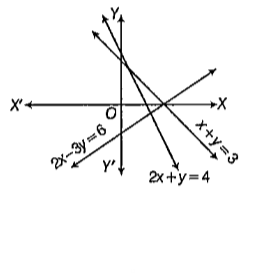 D
D
Draw the graph of the solution set of the inequation 2x+y≥2,x−y≤1,x+2y≤8,x≥0andy≥0
View SolutionConstruct the region represented by the inequations 2x+y≤2andx−3y≤3
View SolutionSolve the following system of linear inequalities
3x+2y≥24,3x+y≤15,x≥4.View SolutionThe graphical solution of linear inequalities x+y≥5 and x−y≤3,
View SolutionThe solution of the system of inequalities x≥0,y≥0,5x+2y≥10,6x+5y≤30 is a polygonal region with the vertices _________
View Solution

