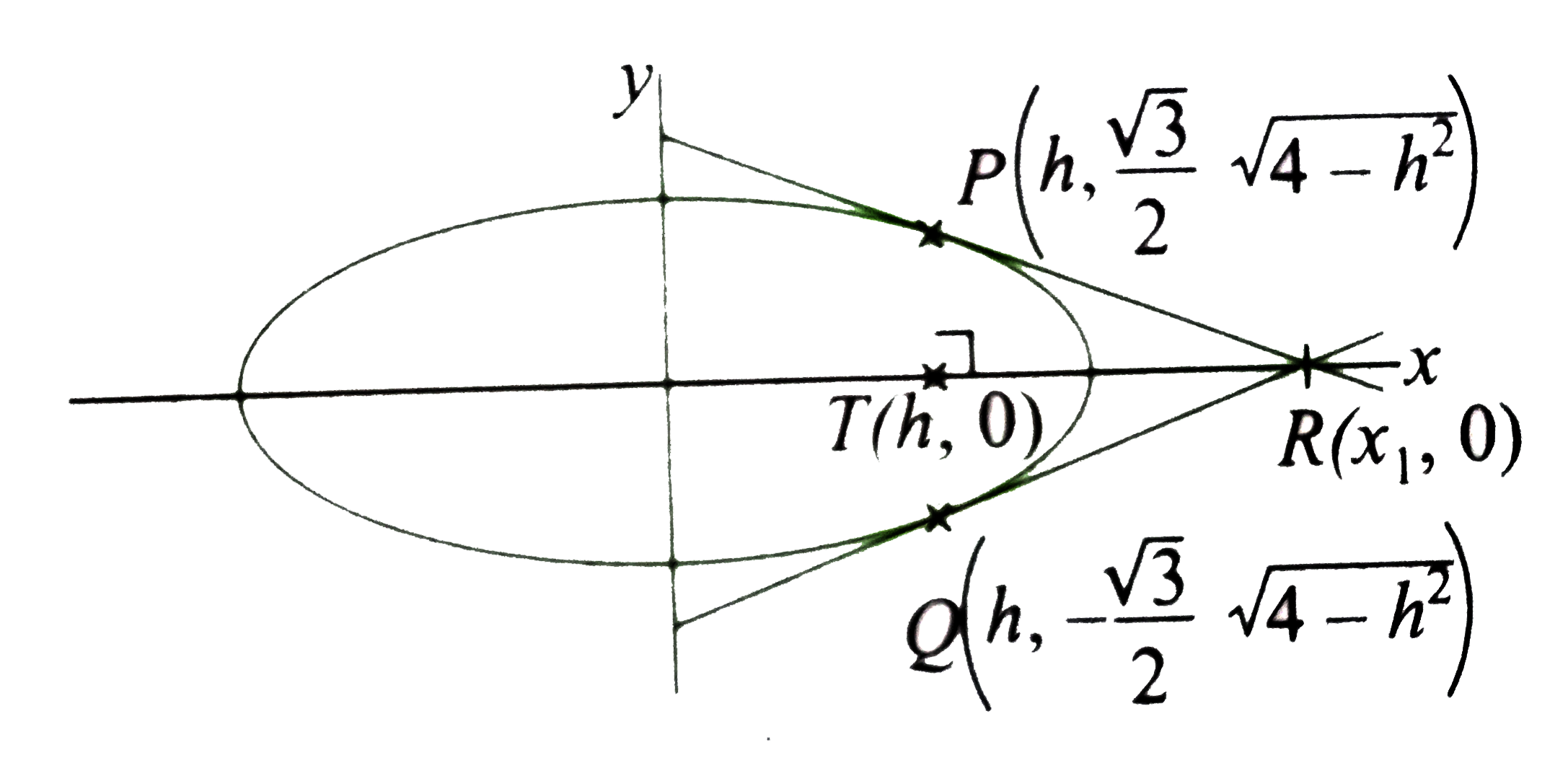
A vertical line passing through the point $(h, 0)$ intersects the ellipse $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ at the points $P$ and $Q$ .Let the tangents to the ellipse at P and Q meet at $R$ . If $Δ (h)$ Area of triangle $Δ P Q R$ , and $Δ_{1} = max \frac{1}{2} \leq h \leq 1 Δ (h)$ and $Δ_{2} = min \frac{1}{2} \leq h \leq 1 Δ (h)$ Then $\frac{8}{\sqrt{5}} Δ_{1} - 8 Δ_{2}$

Text Solution

Verified by Experts

$\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$
$∴ Y = \frac{\sqrt{3}}{2} \sqrt{4 - h^{2}} at x = h$
Let $R (x_{1}, 0)$
PQ, is the chord of contant So, $\frac{x x_{1}}{4} = 1$
or $x = \frac{4}{x_{1}}$
Which is the euation of PQ. At x=h
$\frac{x}{x_{1}} = h or x_{1} = \frac{4}{h}$
$Δ (h) = Area of Δ P Q R = \frac{1}{2} \times P Q \times R T$
$= \frac{1}{2} \times \frac{2 \sqrt{3}}{2} \sqrt{4 - h^{2}} \times (x_{1} - h) = \frac{\sqrt{3}}{2 h} {(4 - h^{2})}^{3 / 2}$
Clearly, $Δ h = \frac{45 \sqrt{5}}{8} at h = \frac{1}{2}$
and $Δ_{2}$ Minimum of $Δ (h) = \frac{9}{2} a t h = 1$
So, $\frac{8}{\sqrt{5}} Δ_{1} - 8 Δ_{2} = \frac{8}{\sqrt{5}} \times \frac{45 \sqrt{5}}{8} - \times \frac{9}{2} = 45 - 36 = 9$

Updated on:21/07/2023