A vertical pole stands at a point A on the boundary of a circular park of radius 2 km and subtends an angle 60∘ at another point B on the boundary. If the chord AB subtends the same angle 60∘ at the centre of the park, the height of the pole is

2√3 km
√3 km
2/√3 kmm
1 km
The correct Answer is:A
Topper's Solved these Questions
- HEIGHTS AND DISTANCES BOOK - MCGROW HILL PUBLICATIONCHAPTER - HEIGHTS AND DISTANCES EXERCISE - SOLVED EXAMPLES (LEVEL 1 ( SINGLE CORRECT ANSWER TYPE QUESTIONS ))
30 Videos
- HEIGHTS AND DISTANCES BOOK - MCGROW HILL PUBLICATIONCHAPTER - HEIGHTS AND DISTANCES EXERCISE - SOLVED EXAMPLES (LEVEL 2 ( SINGLE CORRECT ANSWER TYPE QUESTIONS ))
15 Videos
- ELLIPSEBOOK - MCGROW HILL PUBLICATIONCHAPTER - ELLIPSEEXERCISE - Previous Years B-Architecture Entrance Examination Papers
6 Videos
- HYPERBOLABOOK - MCGROW HILL PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - QUESTION FROM PREVIOUS YEARS. B-ARCHITECTURE ENTRANCE EXAMINATION PAPERS
8 Videos
Similar Questions
A vertical tower PQ subtends the same anlgle of 30∘ at each of two points A and B ,60 m apart on the ground .If AB subtends an angle of 120∘ at p the foot of the tower ,then find the height of the tower .
View SolutionA vertical tower PQ subtends the same anlgle of 30∘ at each of two points A and B ,60 m apart on the ground .If AB subtends an angle of 120∘ at p the foot of the tower ,then find the height of the tower .
View Solution
Knowledge Check
A vertical pole stands at a point A on the boundary of a circular park of radius a and subtends an angle α at another point β on the boundary. If the chord AB subtends an angle α at the centre of the park, the height of the pole is
A2a sinα2tanαB2a cosα2tanαC2a sinα2cotαD2a cosα2cotαA pole stands at a point A on the boundary of a circular park of radius a and subtends an angle α at another point B on the boundary. If the chord AB subtends an angle α at the centre of the path, the height of the pole is
A2acos(α/2)tanαB2asin(α/2)cotαC2asin(α/2)tanαD2acos(α/2)cotαA lamp post standing at a point A on a circular path of radius r subtends an angle α at some point B on the path, and AB subtends an angle of 45∘ at any other point on the path, then height of the lampost is
A√2rcotαB(r/√2)tanαC√2rtanαD(r/√2)cotα
A tower stands at the centre of a circular park . A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60∘ at the foot of the tower , and the angle of elevation of the top of the tower from A or B is 30∘. The height of the tower is
View SolutionO is the centre of a circle of radius 5 cm. The chord AB subtends an angle of 600 at the centre. Find the area of the shaded portion (approximate value).
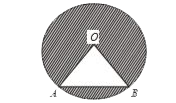
View SolutionA tower stands at the centre of a circular park . A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60∘ at the foot of the tower , and the angle of elevation of the top of the tower from A or B is 30∘. The height of the tower is
View SolutionA tower stands at the centre of a circular park . A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60∘ at the foot of the tower , and the angle of elevation of the top of the tower from A or B is 30∘. The height of the tower is
View SolutionA tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB(=alpha) subtends an angle of elevation of the top of the first tower from A or B is 30∘. The height of the tower is
View Solution
