A well, 2m radius and 40m deep, is being dug. The excavated soil is trasported using a truck of size 5m×2m×πm. How many trips will the truck have to clear the excavated soil if it can be filled to 80% of its height?
10
12
20
24
The correct Answer is:C
To solve the problem step by step, we will calculate the volume of the well, the volume of the truck that can be filled with excavated soil, and then determine how many trips the truck needs to make.
Step 1: Calculate the volume of the well
The well is cylindrical in shape. The formula for the volume V of a cylinder is given by:
V=πr2h
Where:
- r is the radius of the cylinder
- h is the height (or depth) of the cylinder
Given:
- Radius r=2 m
- Depth h=40 m
Substituting the values into the formula:
V=π(22)(40)=π(4)(40)=160π cubic meters
Step 2: Calculate the volume of the truck
The truck is cuboidal in shape. The formula for the volume V of a cuboid is given by:
V=l×b×h
Where:
- l is the length
- b is the breadth
- h is the height
Given:
- Length l=5 m
- Breadth b=2 m
- Height h=5 m
Calculating the total volume of the truck:
V=5×2×5=50 cubic meters
Step 3: Calculate the effective volume of the truck for soil
The truck can only be filled to 80% of its height. Therefore, we need to calculate 80% of the truck's volume:
Effective Volume=50×80100=50×0.8=40 cubic meters
Step 4: Calculate the number of trips required
To find the number of trips the truck needs to make, we divide the total volume of the well by the effective volume of the truck:
Number of trips=Volume of the wellEffective Volume of the truck=160π40
Calculating this gives:
Number of trips=160π40=4π
Since π is approximately 3.14, we can calculate:
4π≈4×3.14=12.56
Since the number of trips must be a whole number, we round up to the nearest whole number, which is 13.
Final Answer
The truck will need to make approximately 13 trips to clear the excavated soil.
---
The well is cylindrical in shape. The formula for the volume V of a cylinder is given by:
- r is the radius of the cylinder
- h is the height (or depth) of the cylinder
- Radius r=2 m
- Depth h=40 m
The truck is cuboidal in shape. The formula for the volume V of a cuboid is given by:
- l is the length
- b is the breadth
- h is the height
- Length l=5 m
- Breadth b=2 m
- Height h=5 m
The truck can only be filled to 80% of its height. Therefore, we need to calculate 80% of the truck's volume:
To find the number of trips the truck needs to make, we divide the total volume of the well by the effective volume of the truck:
The truck will need to make approximately 13 trips to clear the excavated soil.
Topper's Solved these Questions
- BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Grib-In32videos
ADDITIONAL TOPICS IN MATH
- BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATH EXERCISE - PRACTICE TEST24videos
ADDITIONAL TOPICS IN MATH
- BOOK - ENGLISH SATCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE6videos
COMPLEX NUMBERS
Similar Questions
A well of diameter 2 m is dug 14 m deep. The earth taken out of it is spread evenly all around it to form an embankment of height 40 cm. Find the width of the embankment.
View SolutionA uniform box of height 2m and having a square base of side 1m, weight 150kg, is kept on one end on the floor of a truck. The maximum speed with which the truck can round a curve of radius 20m without causing the block to tip over is (assume that friction is sufficient is no sliding).
View SolutionA rectangular diesel tanker is 2m long, 2m wide and 40cm deep. How many litres of diesel can it hold?
View SolutionA cylindrical water tank of diameter 1.4m and height 2.1m is being fed by a pipe of diameter 3.5cm through which water flows at the rate of 2 metre per second. In how much time the tank will be filled?
View SolutionA cylindrical water tank of diameter 1.4m and height 2.1m is being fed by a pipe of diameter 3.5cm through which water flows at the rate of 2 metre per second. In how much time the tank will be filled?
View SolutionA radioactive source, in the form of a metallic sphere of radius 10−2m emits β−particles at the rate of 5×1010 particles per second. The source is electrically insulated. How long will it take for its potential to be raised by 2V, assuming that 40% of the emitted β−particles escape the source.
View SolutionA tank has a hole of area 2cm2 at its bottom and in this hole a conical cork is placed and water is filled up. The water level is made to fall slowly by means of another orifice in the tank. When the water level come to a height of 'H'cm, the conical cork just comes out from the hole. Given, volume of water displaced by the cork =80cm3, mass of the cork =40gm, Area of hole =2cm2, density of water =1gm/cm3. Area of circular cross-section of conical cork =8cm2, Height of cork submerged in water =1207cm. Take g=10m/s2, π=227 and P0=105N/m2.
Calculate the value of H.
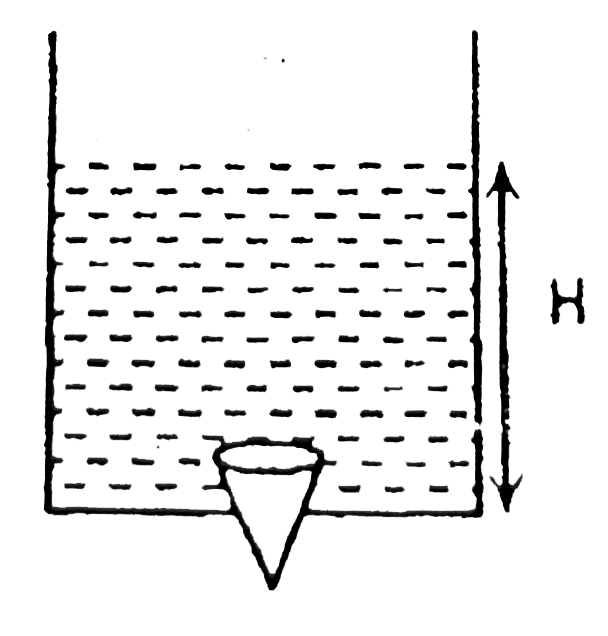 View Solution
View SolutionA tank has a hole of area 2cm2 at its bottom and in this hole a conical cork is placed and water is filled up. The water level is made to fall slowly by means of another orifice in the tank. When the water level come to a height of 'H'cm, the conical cork just comes out from the hole. Given, volume of water displaced by the cork =80cm3, mass of the cork =40gm, Area of hole =2cm2, density of water =1gm/cm3. Area of circular cross-section of conical cork =8cm2, Height of cork submerged in water =1207cm. Take g=10m/s2, π=227 and P0=105N/m2.
Calculate the force exerted by water on the curved surface of the conical cork submerged in water when the liquid level in the vessel is equal to H.
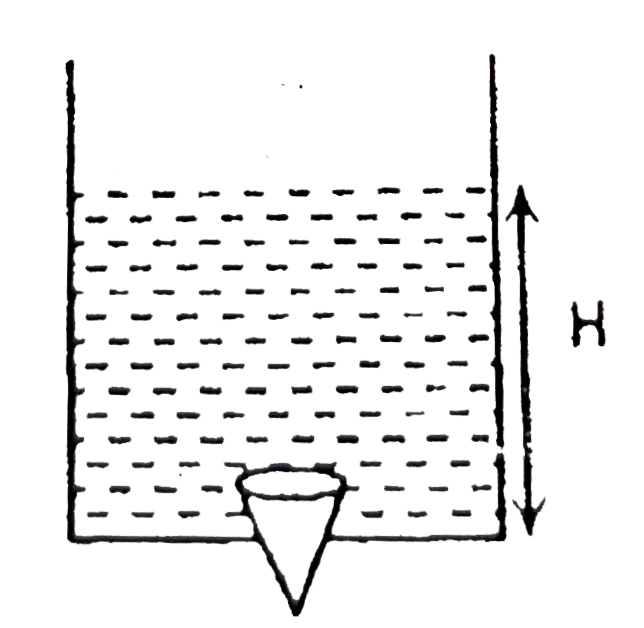 View Solution
View SolutionA tank has a hole of area 2cm2 at its bottom and in this hole a conical cork is placed and water is filled up. The water level is made to fall slowly by means of another orifice in the tank. When the water level come to a height of 'H'cm, the conical cork just comes out from the hole. Given, volume of water displaced by the cork =80cm3, mass of the cork =40gm, Area of hole =2cm2, density of water =1gm/cm3. Area of circular cross-section of conical cork =8cm2, Height of cork submerged in water =1207cm. Take g=10m/s2, π=227 and P0=105N/m2.
The total force exerted by all the fluids on the conical cork in the vertical direction is
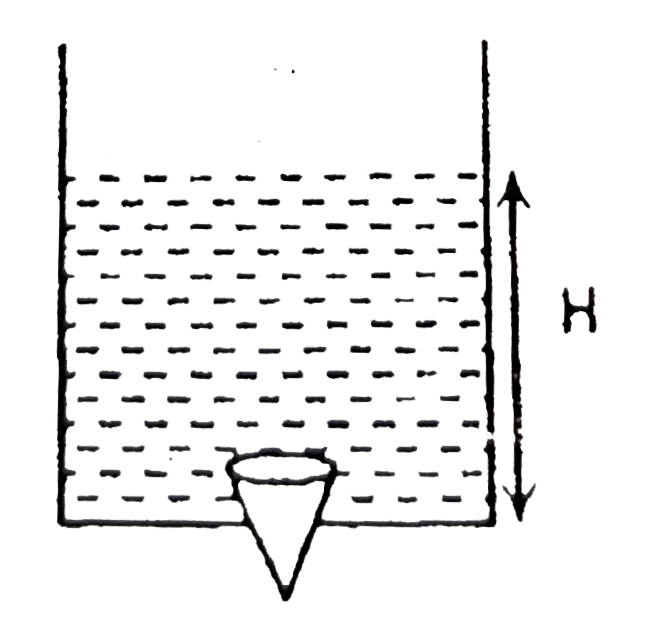 View Solution
View SolutionA student is running at her top speed of 5.0ms−1, to catch a bus, which is stopped at the bus stop. When the student is still 40.0m from the bus, it starts to pull away, moving with a constant acceleration of 0.2ms−2.
a For how much time and what distance does the student have to run at 5.0ms−1 before she overtakes the bus?
b. When she reached the bus, how fast was the bus travelling?
c. Sketch an x−t graph for bothe the student and the bus.
d. Teh equations uou used in part (a)to find the time have a second solution, corresponding to a later time for which the student and the bus are again at thesame place if they continue their specified motions. Explain the significance of this second solution. How fast is the bus travelling at this point?
e. If the students⊤speedis3.5 m s^(-1), will she catch the bus?
f. What is the minimum speed the student must have to just catch up with the bus?For what time and what distance dies she have to run in that case?View Solution

