A wet porous subtance in the open air loses its moisture at a rate proportional to the moisture content. If a sheet hung in the wind loses half its moisture during the first hour, then the time when it would have lost 99.9% of its moisture is (weather conditions remaining same)
(a) more than 100 h
(b) more than 10 h
(c) approximately 10 h
(d) None of these
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Set up the differential equation
Let m(t) be the amount of moisture at time t. According to the problem, the rate of loss of moisture is proportional to the moisture content, which can be expressed as:
dmdt=−km
where k is a positive constant.
Step 2: Separate variables and integrate
We can rearrange the equation to separate the variables:
dmm=−kdt
Now, we integrate both sides:
∫dmm=−k∫dt
This gives us:
ln|m|=−kt+C
where C is the constant of integration.
Step 3: Solve for m(t)
Exponentiating both sides, we have:
m=e−kt+C=eCe−kt
Let N=eC, then:
m(t)=Ne−kt
Step 4: Determine the constant N
At t=0, the initial amount of moisture is m(0)=N. Therefore, we can write:
m(0)=N
Step 5: Use the condition of losing half the moisture in the first hour
We know that after 1 hour, the moisture content is half of the initial amount:
m(1)=N2
Substituting into our equation:
N2=Ne−k⋅1
Dividing both sides by N (assuming N≠0):
12=e−k
Taking the natural logarithm of both sides:
ln(12)=−k⇒k=−ln(2)
Step 6: Find the time when 99.9% of moisture is lost
If 99.9% of the moisture is lost, then 0.1% remains:
m(t)=0.001N
Substituting into our equation:
0.001N=Ne−kt
Dividing both sides by N:
0.001=e−kt
Taking the natural logarithm:
ln(0.001)=−kt
Substituting k=−ln(2):
ln(0.001)=ln(10−3)=−3ln(10)=−(−ln(2))t
Thus:
t=3ln(10)ln(2)
Step 7: Calculate the value of t
Using approximate values:
- ln(10)≈2.302
- ln(2)≈0.693
Calculating:
t≈3×2.3020.693≈6.9060.693≈9.95 hours
Final Answer
Therefore, the time when the substance would have lost 99.9% of its moisture is approximately:
10 hours
Let m(t) be the amount of moisture at time t. According to the problem, the rate of loss of moisture is proportional to the moisture content, which can be expressed as:
dmdt=−km
where k is a positive constant.
We can rearrange the equation to separate the variables:
dmm=−kdt
Now, we integrate both sides:
∫dmm=−k∫dt
This gives us:
ln|m|=−kt+C
where C is the constant of integration.
Exponentiating both sides, we have:
m=e−kt+C=eCe−kt
Let N=eC, then:
m(t)=Ne−kt
At t=0, the initial amount of moisture is m(0)=N. Therefore, we can write:
m(0)=N
We know that after 1 hour, the moisture content is half of the initial amount:
m(1)=N2
Substituting into our equation:
N2=Ne−k⋅1
Dividing both sides by N (assuming N≠0):
12=e−k
Taking the natural logarithm of both sides:
ln(12)=−k⇒k=−ln(2)
If 99.9% of the moisture is lost, then 0.1% remains:
m(t)=0.001N
Substituting into our equation:
0.001N=Ne−kt
Dividing both sides by N:
0.001=e−kt
Taking the natural logarithm:
ln(0.001)=−kt
Substituting k=−ln(2):
ln(0.001)=ln(10−3)=−3ln(10)=−(−ln(2))t
Thus:
t=3ln(10)ln(2)
Using approximate values:
- ln(10)≈2.302
- ln(2)≈0.693
t≈3×2.3020.693≈6.9060.693≈9.95 hours
Therefore, the time when the substance would have lost 99.9% of its moisture is approximately:
10 hours
Topper's Solved these Questions
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise (More Than One Correct Option Type Questions)
13 Videos
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise (Statement I And Ii Type Questions)
9 Videos
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise For Session 5
8 Videos
- DETERMINANTS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DETERMINANTS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
- DIFFERENTIATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIATION EXERCISE - Exercise For Session 10
4 Videos
Similar Questions
A wet porous substance in the open air loses its moisture at a rate proportional to the moisture content. If a sheet hung in the wind loses half of its moisture during the first hour, when will it have lost 95% moisture, if weather conditions remain the same?
View SolutionA certain radioactive material is known to decay at a rate proportional to the amount present. If initially there is 50 kg of the material present and after two hours it is observed that the material has lost 10% of its original mass, find () and expression for the mass of the material remaining at any time t, (ii) the mass of the material after four hours and (iii) the time at which the material has decayed to one half of its initial mass.
View Solution
Knowledge Check
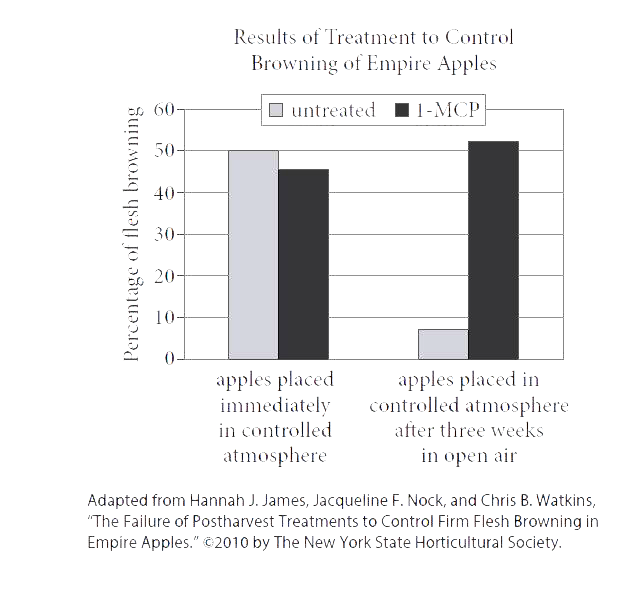
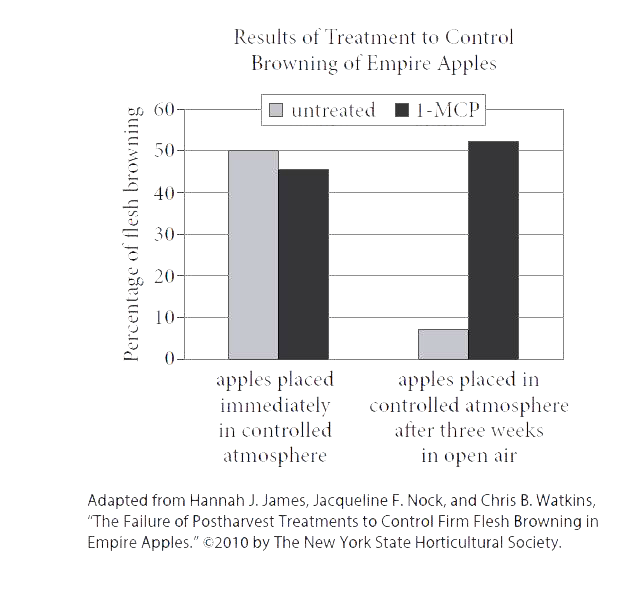
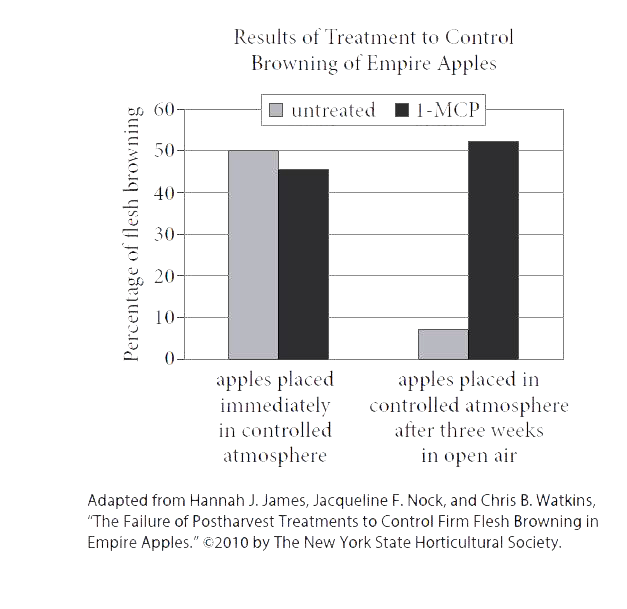
How Do You Like Those Apples? Marketed as SmartFresh, the chemical 1-MCP (1-methylcyclopropene) has been used by fruit growers since 2002 in the United States and elsewhere to preserve the crispness and lengthen the storage life of apples and other fruit, which often must travel long distances before being eaten by consumers. 23 1-MCP lengthens storage life by three to four times when applied to apples. This extended life allows producers to sell their apples in the off-season, months after the apples have been harvested. And at a cost of about one cent per pound of apples, 1-MCP is a highly cost-effective treatment. However, 1-MCP is not a panacea for fruit producers or sellers: there are problems and limitations associated with its use.[1] 1-MCP works by limiting a fruit’s production of ethylene, 24 it is a chemical that causes fruit to ripen and eventually rot. [2] While 1-MCP keeps apples 25 tight and crisp for months, it also limits 26 their scent production. [3] This may not be much of a problem with certain kinds of apples that are not naturally very fragrant, such as Granny Smith, but for apples that are prized for their fruity fragrance, such as McIntosh, this can be a problem with onsumers, 27 that will reject apples lacking the expected aroma. [4] But some fruits do not respond as well to 1-MCP as others 28 did, and some even respond adversely. [5] Furthermore, some fruits, particularly those that naturally produce a large amount of ethylene, do not respond as well to 1-MCP treatment. [6] Take Bartlett 29 pears, for instance, unless they are treated with exactly the right amount of 1-MCP at exactly the right time, they will remain hard and green until they rot, and consumers who experience this will be unlikely to purchase them again. 30 Finally, researchers have found that 1-MCP actually increases susceptibility to some pathologies in certain apple varieties. For example, Empire apples are prone to a condition that causes the flesh of the apple to turn brown. Traditionally, apple producers have dealt with this problem by leaving the apples in the open air for three weeks before storing them in a controlled atmosphere with tightly regulated temperature, humidity, and carbon dioxide levels. As the graph shows, the flesh of untreated Empire apples that are first stored in the open air undergoes 31 roughly five percent less browning than the flesh of untreated Empire apples that are immediately put into storage in a controlled environment. However, when Empire apples are treated with 1-MCP, 32 their flesh turns brown when the apples are first stored in the open air, though not under other conditions. Although researchers continue to search for the right combination of factors that will keep fruits fresh and attractive, 33 the problem may be that consumers are overly concerned with superficial qualities rather than the actual freshness of the fruit.
Which choice most effectively combines the underlined sentences?AWhen applied to apples, 1-MCP lengthens storage life by three to four times, allowing producers to sell their apples in the off-season, months after the apples have been harvested.BProducers are allowed to sell their apples months after they have been harvested—in the off-season—because 1-MCP, when applied to apples, lengthens their storage life by three to four timesC1-MCP lengthens storage life, when applied to apples, by three to four times, allowing producers to sell their apples months after the apples have been harvested in the off-season.DMonths after apples have been harvested, producers are allowed to sell their apples, in the off-season, because 1-MCP lengthens storage life when applied to apples by three to four times.How Do You Like Those Apples? Marketed as SmartFresh, the chemical 1-MCP (1-methylcyclopropene) has been used by fruit growers since 2002 in the United States and elsewhere to preserve the crispness and lengthen the storage life of apples and other fruit, which often must travel long distances before being eaten by consumers. 23 1-MCP lengthens storage life by three to four times when applied to apples. This extended life allows producers to sell their apples in the off-season, months after the apples have been harvested. And at a cost of about one cent per pound of apples, 1-MCP is a highly cost-effective treatment. However, 1-MCP is not a panacea for fruit producers or sellers: there are problems and limitations associated with its use.[1] 1-MCP works by limiting a fruit’s production of ethylene, 24 it is a chemical that causes fruit to ripen and eventually rot. [2] While 1-MCP keeps apples 25 tight and crisp for months, it also limits 26 their scent production. [3] This may not be much of a problem with certain kinds of apples that are not naturally very fragrant, such as Granny Smith, but for apples that are prized for their fruity fragrance, such as McIntosh, this can be a problem with consumers, 27 that will reject apples lacking the expected aroma. [4] But some fruits do not respond as well to 1-MCP as others 28 did, and some even respond adversely. [5] Furthermore, some fruits, particularly those that naturally produce a large amount of ethylene, do not respond as well to 1-MCP treatment. [6] Take Bartlett 29 pears, for instance, unless they are treated with exactly the right amount of 1-MCP at exactly the right time, they will remain hard and green until they rot, and consumers who experience this will be unlikely to purchase them again. 30 Finally, researchers have found that 1-MCP actually increases susceptibility to some pathologies in certain apple varieties. For example, Empire apples are prone to a condition that causes the flesh of the apple to turn brown. Traditionally, apple producers have dealt with this problem by leaving the apples in the open air for three weeks before storing them in a controlled atmosphere with tightly regulated temperature, humidity, and carbon dioxide levels. As the graph shows, the flesh of untreated Empire apples that are first stored in the open air undergoes 31 roughly five percent less browning than the flesh of untreated Empire apples that are immediately put into storage in a controlled environment. However, when Empire apples are treated with 1-MCP, 32 their flesh turns brown when the apples are first stored in the open air, though not under other conditions. Although researchers continue to search for the right combination of factors that will keep fruits fresh and attractive, 33 the problem may be that consumers are overly concerned with superficial qualities rather than the actual freshness of the fruit.
To make this paragraph most logical sentcence 4 should be placedANO CHANGEBafter sentence 1.Cafter sentence 2Dafter sentence 5How Do You Like Those Apples? Marketed as SmartFresh, the chemical 1-MCP (1-methylcyclopropene) has been used by fruit growers since 2002 in the United States and elsewhere to preserve the crispness and lengthen the storage life of apples and other fruit, which often must travel long distances before being eaten by consumers. 23 1-MCP lengthens storage life by three to four times when applied to apples. This extended life allows producers to sell their apples in the off-season, months after the apples have been harvested. And at a cost of about one cent per pound of apples, 1-MCP is a highly cost-effective treatment. However, 1-MCP is not a panacea for fruit producers or sellers: there are problems and limitations associated with its use.[1] 1-MCP works by limiting a fruit’s production of ethylene, 24 it is a chemical that causes fruit to ripen and eventually rot. [2] While 1-MCP keeps apples 25 tight and crisp for months, it also limits 26 their scent production. [3] This may not be much of a problem with certain kinds of apples that are not naturally very fragrant, such as Granny Smith, but for apples that are prized for their fruity fragrance, such as McIntosh, this can be a problem with consumers, 27 that will reject apples lacking the expected aroma. [4] But some fruits do not respond as well to 1-MCP as others 28 did, and some even respond adversely. [5] Furthermore, some fruits, particularly those that naturally produce a large amount of ethylene, do not respond as well to 1-MCP treatment. [6] Take Bartlett 29 pears, for instance, unless they are treated with exactly the right amount of 1-MCP at exactly the right time, they will remain hard and green until they rot, and consumers who experience this will be unlikely to purchase them again. 30 Finally, researchers have found that 1-MCP actually increases susceptibility to some pathologies in certain apple varieties. For example, Empire apples are prone to a condition that causes the flesh of the apple to turn brown. Traditionally, apple producers have dealt with this problem by leaving the apples in the open air for three weeks before storing them in a controlled atmosphere with tightly regulated temperature, humidity, and carbon dioxide levels. As the graph shows, the flesh of untreated Empire apples that are first stored in the open air undergoes 31 roughly five percent less browning than the flesh of untreated Empire apples that are immediately put into storage in a controlled environment. However, when Empire apples are treated with 1-MCP, 32 their flesh turns brown when the apples are first stored in the open air, though not under other conditions. Although researchers continue to search for the right combination of factors that will keep fruits fresh and attractive, 33 the problem may be that consumers are overly concerned with superficial qualities rather than the actual freshness of the fruit.
The writer wants a conclusion that conveys how the shortcomings of 1-MCP presented in the passage affect the actions of people in the fruit industry. Which choice best accomplishes this goal?ANO CHANGEBmany of the improvements to fruit quality they have discovered so far have required trade-offs in other properties of the fruit.Cfor now many fruit sellers must weigh the relative values of aroma, color, and freshness when deciding whether to use 1-MCPDit must be acknowledged that 1-MCP, despite some inadequacies, has enabled the fruit industry to ship and store fruit in ways that were impossible before.
A certain radioactive material is known to decay at a rate proportional to the amount present. If initially there is 50 kg of the material present and after two hours it is observed that the material has lost 10% of its original mass, find () and expression for the mass of the material remaining at any time t, (ii) the mass of the material after four hours and (iii) the time at which the material has decayed to one half of its initial mass.
View SolutionThis passage is adapted from Daniel Chamovitz, What a Plant Knows: A Field Guide to the Senses. ©2012 by Daniel Chamovitz.
The Venus flytrap [Dionaea muscipula] needs to know when an ideal meal is crawling across its leaves. Closing its trap requires a huge expense of energy, and reopening the trap can take several hours, so Dionaea only wants to spring closed when it’s sure that the dawdling insect visiting its surface is large enough to be worth its time. The large black hairs on their lobes allow the Venus flytraps to literally feel their prey, and they act as triggers that spring the trap closed when the proper prey makes its way across the trap. If the insect touches just one hair, the trap will not spring shut, but a large enough bug will likely touch two hairs within about twenty seconds, and that signal springs the Venus flytrap into action.
We can look at this system as analogous to short-term memory. First, the flytrap encodes the information (forms the memory) that something (it doesn’t know what) has touched one of its hairs. Then it stores this information for a number of seconds (retains the memory) and finally retrieves this information (recalls the memory) once a second hair is touched. If a small ant takes a while to get from one hair to the next, the trap will have forgotten the first touch by the time the ant brushes up against the next hair. In other words, it loses the storage of the information, doesn’t close, and the ant happily meanders on. How does the plant encode and store the information from the unassuming bug’s encounter with the first hair? How does it remember the first touch in order to react upon the second?
Scientists have been puzzled by these questions ever since John Burdon-Sanderson’s early report on the physiology of the Venus flytrap in 1882. A century later, Dieter Hodick and Andreas Sievers at the University of Bonn in Germany proposed that the flytrap stored information regarding how many hairs have been touched in the electric charge of its leaf. Their model is quite elegant in its simplicity. In their studies, they discovered that touching a trigger hair on the Venus flytrap causes an electric action potential [a temporary reversal in the electrical polarity of a cell membrane] that induces calcium channels to open in the trap (this coupling of action potentials and the opening of calcium channels is similar to the processes that occur during communication between human neurons), thus causing a rapid increase in the concentration of calcium ions.
They proposed that the trap requires a relatively high concentration of calcium in order to close and that a single action potential from just one trigger hair being touched does not reach this level. Therefore, a second hair needs to be stimulated to push the calcium concentration over this threshold and spring the trap. The encoding of the information requires maintaining a high enough level of calcium so that a second increase (triggered by touching the second hair) pushes the total concentration of calcium over the threshold. As the calcium ion concentrations dissipate over time, if the second touch and potential don’t happen quickly, the final concentration after the second trigger won’t be high enough to close the trap, and the memory is lost.
Subsequent research supports this model. Alexander Volkov and his colleagues at Oakwood University in Alabama first demonstrated that it is indeed electricity that causes the Venus flytrap to close. To test the model they rigged up very fine electrodes and applied an electrical current to the open lobes of the trap. This made the trap close without any direct touch to its trigger hairs (while they didn’t measure calcium levels, the current likely led to increases). When they modified this experiment by altering the amount of electrical current, Volkov could determine the exact electrical charge needed for the trap to close. As long as fourteen microcoulombs—a tiny bit more than the static electricity generated by rubbing two balloons together—flowed between the two electrodes, the trap closed. This could come as one large burst or as a series of smaller charges within twenty seconds. If it took longer than twenty seconds to accumulate the total charge, the trap would remain open.
Which choice provides the best evidence for the answer to the previous question?
View SolutionThis passage is adapted from Daniel Chamovitz, What a Plant Knows: A Field Guide to the Senses. ©2012 by Daniel Chamovitz.
The Venus flytrap [Dionaea muscipula] needs to know when an ideal meal is crawling across its leaves. Closing its trap requires a huge expense of energy, and reopening the trap can take several hours, so Dionaea only wants to spring closed when it’s sure that the dawdling insect visiting its surface is large enough to be worth its time. The large black hairs on their lobes allow the Venus flytraps to literally feel their prey, and they act as triggers that spring the trap closed when the proper prey makes its way across the trap. If the insect touches just one hair, the trap will not spring shut, but a large enough bug will likely touch two hairs within about twenty seconds, and that signal springs the Venus flytrap into action.
We can look at this system as analogous to short-term memory. First, the flytrap encodes the information (forms the memory) that something (it doesn’t know what) has touched one of its hairs. Then it stores this information for a number of seconds (retains the memory) and finally retrieves this information (recalls the memory) once a second hair is touched. If a small ant takes a while to get from one hair to the next, the trap will have forgotten the first touch by the time the ant brushes up against the next hair. In other words, it loses the storage of the information, doesn’t close, and the ant happily meanders on. How does the plant encode and store the information from the unassuming bug’s encounter with the first hair? How does it remember the first touch in order to react upon the second?
Scientists have been puzzled by these questions ever since John Burdon-Sanderson’s early report on the physiology of the Venus flytrap in 1882. A century later, Dieter Hodick and Andreas Sievers at the University of Bonn in Germany proposed that the flytrap stored information regarding how many hairs have been touched in the electric charge of its leaf. Their model is quite elegant in its simplicity. In their studies, they discovered that touching a trigger hair on the Venus flytrap causes an electric action potential [a temporary reversal in the electrical polarity of a cell membrane] that induces calcium channels to open in the trap (this coupling of action potentials and the opening of calcium channels is similar to the processes that occur during communication between human neurons), thus causing a rapid increase in the concentration of calcium ions.
They proposed that the trap requires a relatively high concentration of calcium in order to close and that a single action potential from just one trigger hair being touched does not reach this level. Therefore, a second hair needs to be stimulated to push the calcium concentration over this threshold and spring the trap. The encoding of the information requires maintaining a high enough level of calcium so that a second increase (triggered by touching the second hair) pushes the total concentration of calcium over the threshold. As the calcium ion concentrations dissipate over time, if the second touch and potential don’t happen quickly, the final concentration after the second trigger won’t be high enough to close the trap, and the memory is lost.
Subsequent research supports this model. Alexander Volkov and his colleagues at Oakwood University in Alabama first demonstrated that it is indeed electricity that causes the Venus flytrap to close. To test the model they rigged up very fine electrodes and applied an electrical current to the open lobes of the trap. This made the trap close without any direct touch to its trigger hairs (while they didn’t measure calcium levels, the current likely led to increases). When they modified this experiment by altering the amount of electrical current, Volkov could determine the exact electrical charge needed for the trap to close. As long as fourteen microcoulombs—a tiny bit more than the static electricity generated by rubbing two balloons together—flowed between the two electrodes, the trap closed. This could come as one large burst or as a series of smaller charges within twenty seconds. If it took longer than twenty seconds to accumulate the total charge, the trap would remain open.
According to the passage, which statement best explains why the Venus flytrap requires a second trigger hair to be touched within a short amount of time in order for its trap to close?
View SolutionThis passage is adapted from Daniel Chamovitz, What a Plant Knows: A Field Guide to the Senses. ©2012 by Daniel Chamovitz.
The Venus flytrap [Dionaea muscipula] needs to know when an ideal meal is crawling across its leaves. Closing its trap requires a huge expense of energy, and reopening the trap can take several hours, so Dionaea only wants to spring closed when it’s sure that the dawdling insect visiting its surface is large enough to be worth its time. The large black hairs on their lobes allow the Venus flytraps to literally feel their prey, and they act as triggers that spring the trap closed when the proper prey makes its way across the trap. If the insect touches just one hair, the trap will not spring shut, but a large enough bug will likely touch two hairs within about twenty seconds, and that signal springs the Venus flytrap into action.
We can look at this system as analogous to short-term memory. First, the flytrap encodes the information (forms the memory) that something (it doesn’t know what) has touched one of its hairs. Then it stores this information for a number of seconds (retains the memory) and finally retrieves this information (recalls the memory) once a second hair is touched. If a small ant takes a while to get from one hair to the next, the trap will have forgotten the first touch by the time the ant brushes up against the next hair. In other words, it loses the storage of the information, doesn’t close, and the ant happily meanders on. How does the plant encode and store the information from the unassuming bug’s encounter with the first hair? How does it remember the first touch in order to react upon the second?
Scientists have been puzzled by these questions ever since John Burdon-Sanderson’s early report on the physiology of the Venus flytrap in 1882. A century later, Dieter Hodick and Andreas Sievers at the University of Bonn in Germany proposed that the flytrap stored information regarding how many hairs have been touched in the electric charge of its leaf. Their model is quite elegant in its simplicity. In their studies, they discovered that touching a trigger hair on the Venus flytrap causes an electric action potential [a temporary reversal in the electrical polarity of a cell membrane] that induces calcium channels to open in the trap (this coupling of action potentials and the opening of calcium channels is similar to the processes that occur during communication between human neurons), thus causing a rapid increase in the concentration of calcium ions.
They proposed that the trap requires a relatively high concentration of calcium in order to close and that a single action potential from just one trigger hair being touched does not reach this level. Therefore, a second hair needs to be stimulated to push the calcium concentration over this threshold and spring the trap. The encoding of the information requires maintaining a high enough level of calcium so that a second increase (triggered by touching the second hair) pushes the total concentration of calcium over the threshold. As the calcium ion concentrations dissipate over time, if the second touch and potential don’t happen quickly, the final concentration after the second trigger won’t be high enough to close the trap, and the memory is lost.
Subsequent research supports this model. Alexander Volkov and his colleagues at Oakwood University in Alabama first demonstrated that it is indeed electricity that causes the Venus flytrap to close. To test the model they rigged up very fine electrodes and applied an electrical current to the open lobes of the trap. This made the trap close without any direct touch to its trigger hairs (while they didn’t measure calcium levels, the current likely led to increases). When they modified this experiment by altering the amount of electrical current, Volkov could determine the exact electrical charge needed for the trap to close. As long as fourteen microcoulombs—a tiny bit more than the static electricity generated by rubbing two balloons together—flowed between the two electrodes, the trap closed. This could come as one large burst or as a series of smaller charges within twenty seconds. If it took longer than twenty seconds to accumulate the total charge, the trap would remain open.
Based on the passage, a significant advantage of the Venus flytrap’s requirement for multiple triggers is that it
View SolutionThis passage is adapted from Daniel Chamovitz, What a Plant Knows: A Field Guide to the Senses. ©2012 by Daniel Chamovitz.
The Venus flytrap [Dionaea muscipula] needs to know when an ideal meal is crawling across its leaves. Closing its trap requires a huge expense of energy, and reopening the trap can take several hours, so Dionaea only wants to spring closed when it’s sure that the dawdling insect visiting its surface is large enough to be worth its time. The large black hairs on their lobes allow the Venus flytraps to literally feel their prey, and they act as triggers that spring the trap closed when the proper prey makes its way across the trap. If the insect touches just one hair, the trap will not spring shut, but a large enough bug will likely touch two hairs within about twenty seconds, and that signal springs the Venus flytrap into action.
We can look at this system as analogous to short-term memory. First, the flytrap encodes the information (forms the memory) that something (it doesn’t know what) has touched one of its hairs. Then it stores this information for a number of seconds (retains the memory) and finally retrieves this information (recalls the memory) once a second hair is touched. If a small ant takes a while to get from one hair to the next, the trap will have forgotten the first touch by the time the ant brushes up against the next hair. In other words, it loses the storage of the information, doesn’t close, and the ant happily meanders on. How does the plant encode and store the information from the unassuming bug’s encounter with the first hair? How does it remember the first touch in order to react upon the second?
Scientists have been puzzled by these questions ever since John Burdon-Sanderson’s early report on the physiology of the Venus flytrap in 1882. A century later, Dieter Hodick and Andreas Sievers at the University of Bonn in Germany proposed that the flytrap stored information regarding how many hairs have been touched in the electric charge of its leaf. Their model is quite elegant in its simplicity. In their studies, they discovered that touching a trigger hair on the Venus flytrap causes an electric action potential [a temporary reversal in the electrical polarity of a cell membrane] that induces calcium channels to open in the trap (this coupling of action potentials and the opening of calcium channels is similar to the processes that occur during communication between human neurons), thus causing a rapid increase in the concentration of calcium ions.
They proposed that the trap requires a relatively high concentration of calcium in order to close and that a single action potential from just one trigger hair being touched does not reach this level. Therefore, a second hair needs to be stimulated to push the calcium concentration over this threshold and spring the trap. The encoding of the information requires maintaining a high enough level of calcium so that a second increase (triggered by touching the second hair) pushes the total concentration of calcium over the threshold. As the calcium ion concentrations dissipate over time, if the second touch and potential don’t happen quickly, the final concentration after the second trigger won’t be high enough to close the trap, and the memory is lost.
Subsequent research supports this model. Alexander Volkov and his colleagues at Oakwood University in Alabama first demonstrated that it is indeed electricity that causes the Venus flytrap to close. To test the model they rigged up very fine electrodes and applied an electrical current to the open lobes of the trap. This made the trap close without any direct touch to its trigger hairs (while they didn’t measure calcium levels, the current likely led to increases). When they modified this experiment by altering the amount of electrical current, Volkov could determine the exact electrical charge needed for the trap to close. As long as fourteen microcoulombs—a tiny bit more than the static electricity generated by rubbing two balloons together—flowed between the two electrodes, the trap closed. This could come as one large burst or as a series of smaller charges within twenty seconds. If it took longer than twenty seconds to accumulate the total charge, the trap would remain open.
The use of the phrases “dawdling insect” (line 6), “happily meanders” (line 27), and “unassuming bug’s encounter” (lines 28-29) in the first two paragraphs establishes a tone that is
View Solution
