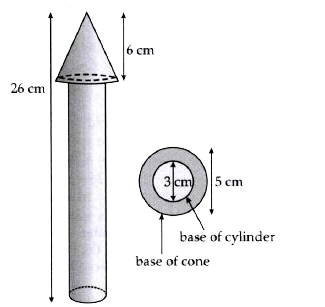
A wooden toy rocket is in the shape of a cone mounted on a cylinder as shown in Fig. 16.36. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours. (Take π=3.14 )
To solve the problem of finding the area of the wooden toy rocket that is painted in two different colors, we need to calculate the surface areas of the conical and cylindrical portions separately.
Step 1: Identify the dimensions of the rocket
- Height of the entire rocket (cylinder + cone) = 26 cm
- Height of the conical part = 6 cm
- Therefore, height of the cylindrical part = 26 cm - 6 cm = 20 cm
- Diameter of the conical portion = 5 cm, so radius of the cone (r_cone) = 5 cm / 2 = 2.5 cm
- Diameter of the cylindrical portion = 3 cm, so radius of the cylinder (r_cylinder) = 3 cm / 2 = 1.5 cm
Step 2: Calculate the slant height of the cone
The slant height (l) of the cone can be calculated using the Pythagorean theorem:
l=√(rcone)2+(heightcone)2
l=√(2.5)2+(6)2=√6.25+36=√42.25≈6.5cm
Step 3: Calculate the curved surface area of the cone
The formula for the curved surface area (CSA) of a cone is given by:
CSAcone=πrconel
Substituting the values:
CSAcone=3.14×2.5×6.5
CSAcone≈3.14×16.25≈51.025cm2
Step 4: Calculate the base area of the cone
The base area (BA) of the cone is given by:
BAcone=π(rcone)2
Substituting the values:
BAcone=3.14×(2.5)2
BAcone=3.14×6.25≈19.625cm2
Step 5: Calculate the curved surface area of the cylinder
The formula for the curved surface area of a cylinder is given by:
CSAcylinder=2πrcylinderhcylinder
Substituting the values:
CSAcylinder=2×3.14×1.5×20
CSAcylinder=2×3.14×30≈188.4cm2
Step 6: Calculate the base area of the cylinder
The base area of the cylinder is given by:
BAcylinder=π(rcylinder)2
Substituting the values:
BAcylinder=3.14×(1.5)2
BAcylinder=3.14×2.25≈7.065cm2
Step 7: Calculate the total area painted orange (cone)
The area painted orange includes the curved surface area of the cone and the base area of the cone:
Areaorange=CSAcone+BAcone
Areaorange=51.025+19.625≈70.65cm2
Step 8: Calculate the total area painted yellow (cylinder)
The area painted yellow includes the curved surface area of the cylinder and the base area of the cylinder, minus the base area of the cone:
Areayellow=CSAcylinder+BAcylinder−BAcone
Areayellow=188.4+7.065−19.625
Areayellow=188.4+7.065−19.625≈175.84cm2
Final Answer
- Area painted orange (cone) = 70.65 cm²
- Area painted yellow (cylinder) = 175.84 cm²
- Height of the entire rocket (cylinder + cone) = 26 cm
- Height of the conical part = 6 cm
- Therefore, height of the cylindrical part = 26 cm - 6 cm = 20 cm
- Diameter of the conical portion = 5 cm, so radius of the cone (r_cone) = 5 cm / 2 = 2.5 cm
- Diameter of the cylindrical portion = 3 cm, so radius of the cylinder (r_cylinder) = 3 cm / 2 = 1.5 cm
The slant height (l) of the cone can be calculated using the Pythagorean theorem:
l=√(rcone)2+(heightcone)2
l=√(2.5)2+(6)2=√6.25+36=√42.25≈6.5cm
The formula for the curved surface area (CSA) of a cone is given by:
CSAcone=πrconel
Substituting the values:
CSAcone=3.14×2.5×6.5
CSAcone≈3.14×16.25≈51.025cm2
The base area (BA) of the cone is given by:
BAcone=π(rcone)2
Substituting the values:
BAcone=3.14×(2.5)2
BAcone=3.14×6.25≈19.625cm2
The formula for the curved surface area of a cylinder is given by:
CSAcylinder=2πrcylinderhcylinder
Substituting the values:
CSAcylinder=2×3.14×1.5×20
CSAcylinder=2×3.14×30≈188.4cm2
The base area of the cylinder is given by:
BAcylinder=π(rcylinder)2
Substituting the values:
BAcylinder=3.14×(1.5)2
BAcylinder=3.14×2.25≈7.065cm2
The area painted orange includes the curved surface area of the cone and the base area of the cone:
Areaorange=CSAcone+BAcone
Areaorange=51.025+19.625≈70.65cm2
The area painted yellow includes the curved surface area of the cylinder and the base area of the cylinder, minus the base area of the cone:
Areayellow=CSAcylinder+BAcylinder−BAcone
Areayellow=188.4+7.065−19.625
Areayellow=188.4+7.065−19.625≈175.84cm2
- Area painted orange (cone) = 70.65 cm²
- Area painted yellow (cylinder) = 175.84 cm²
Topper's Solved these Questions
Similar Questions
A wooden toy rocket is in the shape of a cone mounted on a cylinder, as shown in figure. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical partition has a diameter of 5 cm, while the base diameter of the cylindrical protion is 3 cm.Find the slant height of conical portion.
View SolutionA wooden toy rocket is in the shape of a cone mounted on a cylinder. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours.
View Solution
Knowledge Check
The height of a conical tank is 60 cm and the diameter of its base is 64 cm. The cost of painting it from outside at the rate of Rs35 per sq m is
ARs52.00 (approx)BRs39.20 (approx)CRs35.20 (approx)DRs23.94 (approx)The diameter of the base of a cylinder is 6 cm and its height is 14 cm. The volume of the cylinder is
A198cm3B396cm3C495cm3D297cm3
A wooden toy rocket is in the shape of a cone mounted on a cylinder, as shown in figure. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical partition has a diameter of 5 cm, while the base diameter of the cylindrical protion is 3 cm.
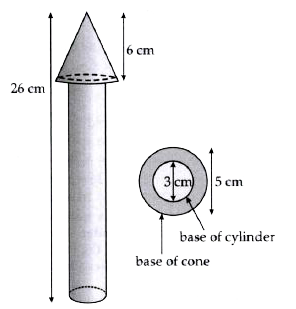
If the conical portion is to be painted orange, find the area to be painted orange. Find the area of the rockeeet peainted with each of these colours? (Take π = 3.14)
View SolutionA wooden toy is in the shape of a cone mounted on a cylinder as shown alongside If the height of the cone is 24 cm the total height of the toy is 60 cm and the radius of the base of the cone= twice the radius of the base of the cylinder = 10 cm .Find the total surface area of the you.

View SolutionA toy is in the shape of a cone mounted on a hemisphere of same base radius. If the volume of the toy is 231 cm3 and its diameter is 7 cm, find the height of the toy
View SolutionA toy is in the form of a cone mounted on the hemisphere with the same radius. The diameter of the base of the conical portion is 12 cm and its height is 8 cm.
What is the volume of the toy?
View SolutionThe curve surface area of a cylinder is 1320cm2 and its base has diameter 21 cm,then the height of the cylinder is
View SolutionA toy is in the form of a cone mounted on the hemisphere with the same radius. The diameter of the base of the conical portion is 12 cm and its height is 8 cm.
What is the total surface area of the toy?
View Solution
