is a right triangle right-angled at . Prove that
To prove that angle ABC is 60 degrees in triangle ABC, where C is the right angle and AC = √3 * BC, we can follow these steps:
1. Identify the triangle and given information:
- Triangle ABC is a right triangle with the right angle at C.
- We are given that AC = √3 * BC.
2. Use the tangent function:
- For angle A, we can use the tangent function, which is defined as the ratio of the opposite side to the adjacent side.
- In triangle ABC, for angle A:
tanA=oppositeadjacent=BCAC
3. Substitute the given values:
- We know that AC = √3 * BC. Therefore:
tanA=BC√3⋅BC
- Simplifying this gives:
tanA=1√3
4. Find angle A:
- The value of angle A for which tan A = 1/√3 is:
A=30∘
5. Use the triangle sum property:
- In any triangle, the sum of the angles is 180 degrees. Therefore:
A+B+C=180∘
- Substituting the known values:
30∘+B+90∘=180∘
6. Solve for angle B:
- Rearranging gives:
B=180∘−30∘−90∘=60∘
7. Conclusion:
- Therefore, we have proved that:
∠ABC=60∘
- Triangle ABC is a right triangle with the right angle at C.
- We are given that AC = √3 * BC.
- For angle A, we can use the tangent function, which is defined as the ratio of the opposite side to the adjacent side.
- In triangle ABC, for angle A:
tanA=oppositeadjacent=BCAC
- We know that AC = √3 * BC. Therefore:
tanA=BC√3⋅BC
- Simplifying this gives:
tanA=1√3
- The value of angle A for which tan A = 1/√3 is:
A=30∘
- In any triangle, the sum of the angles is 180 degrees. Therefore:
A+B+C=180∘
- Substituting the known values:
30∘+B+90∘=180∘
- Rearranging gives:
B=180∘−30∘−90∘=60∘
- Therefore, we have proved that:
∠ABC=60∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In a right triangle ABC, right angled at C, if a = 7 cm and b = 7√3 cm, then ∠A=
A30∘B60∘C45∘Dnone of these - Question 2 - Select One
In a right angled triangle a2+b2+c2 is :
AR2B4R2C8R2Dnone of these - Question 3 - Select One
Let △ABC is a right angled triangle right angled at A such that A(1,2),C(3,1) and area of △ABC=5√5 then abscissa of B can be
A1+5√2B1+2√5C1−5√2D3+2√5
if in triangle ABC right angled at C then tanA+tanB
View SolutionIn figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) ΔABC~ΔAMP (ii) CAPA=BCMP
 View Solution
View SolutionIn fig.41, ABC is a right triangle right angled at A. D lies on BA produced and DE⊥BC, intersecting AC at F . if ∠AFE=1300, find ∠BDE (ii) ∠BCA ∠ABC
View SolutionGiven aΔABC in which ∠B=90∘andAB=√3BC. Prove that ∠C=60∘
View SolutionABC is a right triangles right angled at C . Let BC =a ,CA=b, AB = c, and p be the length of perpendicular from C to AB . Prove that cp = ab .
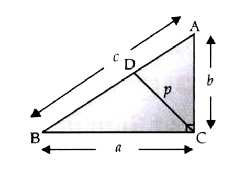 View Solution
View Solution

