A(1,4)andB(4,8) are two points. P is a point on AB such that AP=AB+BP. If AP=10, find the coordinates of P.
To find the coordinates of point P on line segment AB such that AP=AB+BP and AP=10, we can follow these steps:
Step 1: Identify the coordinates of points A and B
The coordinates of point A are (1,4) and the coordinates of point B are (4,8).
Step 2: Calculate the distance AB
We can use the distance formula to find the distance between points A and B:
AB=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of A and B:
AB=√(4−1)2+(8−4)2=√32+42=√9+16=√25=5
Step 3: Set up the equation based on the given condition
We know that:
AP=AB+BP
Given AP=10 and AB=5, we can substitute these values into the equation:
10=5+BP
From this, we can solve for BP:
BP=10−5=5
Step 4: Determine the relationship between points A, B, and P
Since AP=10 and BP=5, and both segments are equal, point B must be the midpoint of segment AP. Therefore, we can express the coordinates of point P as:
P=(x,y)
Step 5: Use the midpoint formula
The midpoint M of segment AP can be calculated as:
M=(xA+xP2,yA+yP2)
Since B is the midpoint, we can set up the equations:
1+x2=4(for x-coordinates)
4+y2=8(for y-coordinates)
Step 6: Solve for x and y
From the first equation:
1+x=8⟹x=8−1=7
From the second equation:
4+y=16⟹y=16−4=12
Conclusion
The coordinates of point P are (7,12).
The coordinates of point A are (1,4) and the coordinates of point B are (4,8).
We can use the distance formula to find the distance between points A and B:
AB=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of A and B:
AB=√(4−1)2+(8−4)2=√32+42=√9+16=√25=5
We know that:
AP=AB+BP
Given AP=10 and AB=5, we can substitute these values into the equation:
10=5+BP
From this, we can solve for BP:
BP=10−5=5
Since AP=10 and BP=5, and both segments are equal, point B must be the midpoint of segment AP. Therefore, we can express the coordinates of point P as:
P=(x,y)
The midpoint M of segment AP can be calculated as:
M=(xA+xP2,yA+yP2)
Since B is the midpoint, we can set up the equations:
1+x2=4(for x-coordinates)
4+y2=8(for y-coordinates)
From the first equation:
1+x=8⟹x=8−1=7
From the second equation:
4+y=16⟹y=16−4=12
The coordinates of point P are (7,12).
Similar Questions
If A=(2, -3, 7), B = (-1, 4, -5) and P is a point
on the line AB such that AP:BP=3:2 then P
has the coordinates
View SolutionP is a point on the line joining A (4, 3) and B (-2, 6) such that 5AP = 2BP. Find the coordinates of P.
View SolutionThe line joining the points A (-3, -10) and B (-2, 6) is divided by the point P such that PBAB=15. Find the co-ordinates of P.
View SolutionIf a point P lies on the line segment joining points A(−3,4)andB(−2,−6) such that 2AP=3BP
then, find the co-ordinates of point P.
View SolutionIf A=(2,3), B=(-2-5), C=(-4,6) and if P is a point on BC such that AP bisects the angle A, then find P.
View SolutionA line segment AB is 8 cm in length. AB is produced to P such that BP2=AB.AP, find the length of BP.
View SolutionGiven a triangle ABC in which A = (4, -4) B = (0,5) and C = (5, 10). A point P lies on BC such that BP : PC = 3 : 2. Find the length of line segment AP.
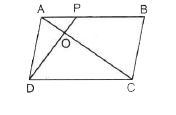
View SolutionThe given figure shows a parallelogram ABCD with area 324sq. cm. P is a point in AB such that AP:PB= 1:2. Find the area of ΔAPD.
View SolutionP(1, -2) is a point on the line segment A(3, -6) and B(x, y) such that AP:PB is equal to 2:3. Find the coordinates of B.
View SolutionA rod of AB of length 3 rests on a wall as follows :
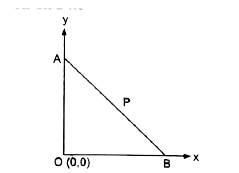
P is a point on AB such that AP:PB=1:2 If the rod slides along the wall, then the locus of P lies on
View Solution
