are vertices of If 'P' is the point inside the , such that min. . Then the maximum of is.(where represent distance between .
1
2
none of these
We have ,
d (P , BC) min {d (P, AB) , d(P, AC)}
d (P , BC) d (P , AB) and d (P, BC) d(P , AC)
Thus , d (P , BC) is maximum when
d (P , BC ) = d (P, AB) = d(P , AC)
P coincides with the incentre of .
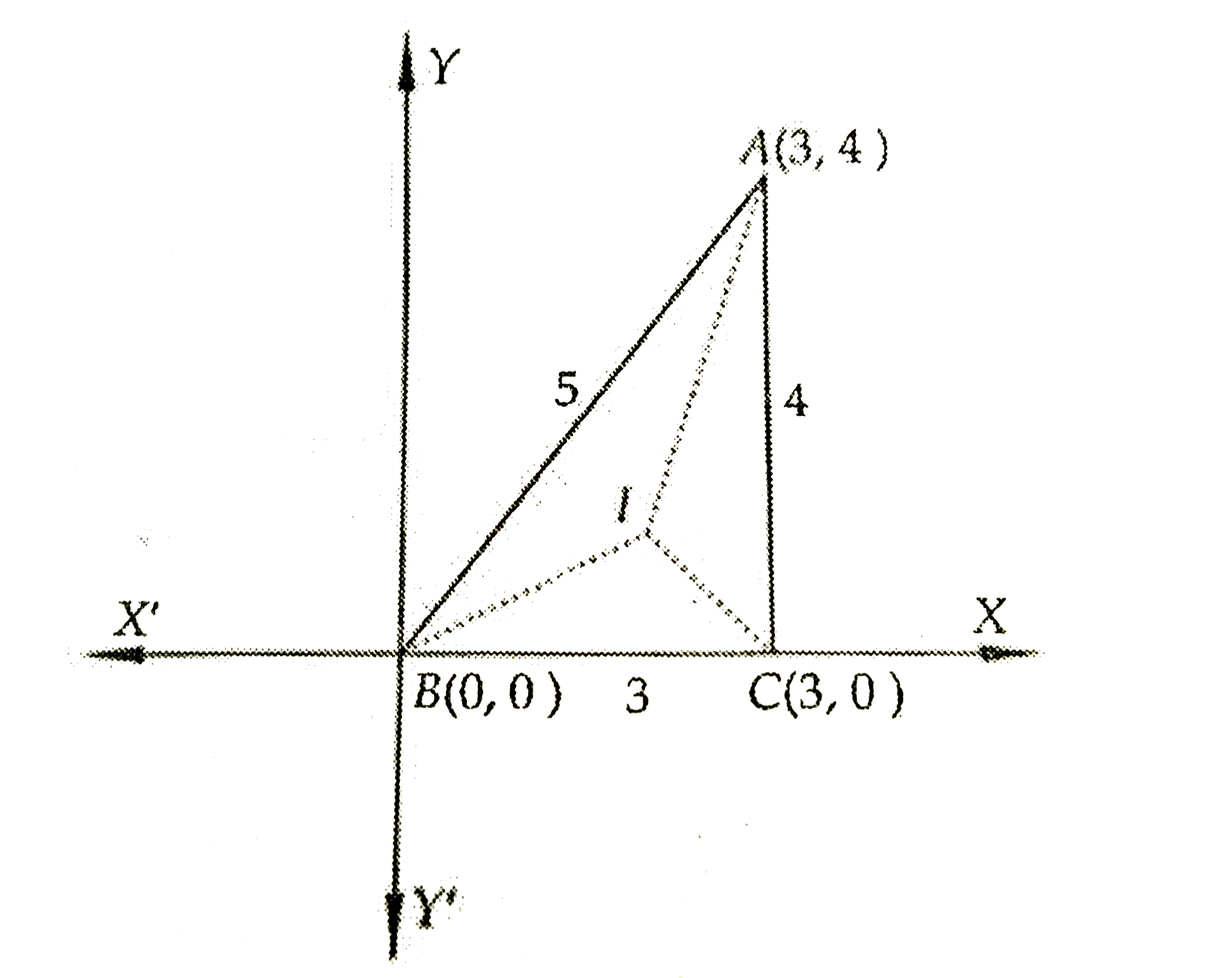
Maximum value of d (P , BC)
= y-coordinate of the incentre of
Topper's Solved these Questions
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMACHAPTER - STRAIGHT LINESEXERCISE - Section-1 Solved MCQs (Example)
1 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMACHAPTER - STRAIGHT LINESEXERCISE - SECTION - II (ASSERTION - REASON TYPE MCQs)
14 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMACHAPTER - STRAIGHT LINESEXERCISE - ILLUSTRATION 18
1 Videos
- SETSBOOK - OBJECTIVE RD SHARMACHAPTER - SETSEXERCISE - Chapter Test
30 Videos
Similar Questions
In ΔABC, if D is any point on the side BC, show that (AB+BC+AC)>2AD.

View SolutionLet O(0.0),A(6,0) and B(3,√3) be the vertices of △OAB. Let R those points P inside △OAB which satisfy d(P, OA) minimum (d(P,OB),d(P,AB) where d(P, OA), d(P, OB) and d(P, AB) represent the distance of P from the sides OA, OB and AFB respectively. If the area of region R is 9(a−√b) where a and b are coprime, then find the value of (a+ b)
View Solution
Knowledge Check
Let O(0, 0) and B(1,1√3) be the vertices of a triangle. Let R be the region consisting of all those points P inside ΔOAB satisfying. d(P,OA)lr min {d(P,OB),d(P,AB)}, where d denotes the distance from the point P to the corresponding line. Let M be peak of region R.
The perimeter of region R is equal toA√3B1√3C3D2−√3Let O(0,0),A(2,0)andB(1,1√3) be the vertices of a triangle. Let R be the region consisting of all those points P inside ΔOAB satisfying. d(P,OA)lr min {d(P,OB),d(P,AB)}, where d denotes the distance from the point P to the corresponding line. Let M be peak of region R. The perimeter of region R is equal to
A4−√3B4+√3C4+3√3D2+4√(2−√3)D is any point on side AC of ΔABC. If P,Q, X, Y are the mid points of AB,BC,ADandDCrespectively, then the ratio of PXandQYis
A1:2B1:1C2:1D2:3
Consider a rectangle ABCD formed by the points A=(0,0), B= (6, 0), C =(6, 4) and D =(0,4), P (x, y) is a moving interior point of the rectangle, moving in such a way that d(P,AB)≤min{d(P,BC),d(P,CD)andd(P,AD)} here d (P, AB), d (P, BC), d (P, CD) and d (P, AD) represent the distance of the point P from the sides AB, BC, CD and AD respectively. Area of the region representing all possible positions of the point P is equal to
View SolutionA(4,3),B(6,5)andC(5,−2) are the vertices of a ΔABC, if P is a point on BC such that BP:PC=2:3. Find the co-ordinates of P and then prove then ar (ΔABP):ar(ΔACP)=2:3.
View SolutionP and Q are the points on sides AB and AC respectively of a ΔABC , such that PQ||BC .If AP∣PB=2:3 and AQ=4 cm , then the length of AC is ….. Cm .
View SolutionIn the figure, ΔABC~ΔBPQ. If AB = BC and P is the midpoint of seg BC, then A(ΔABC):A(ΔBPQ)=
View SolutionIn a ΔABC the bisector of angles BandC lie along the lines x=yandy=0. If A is (1,2), then √10d(A,BC) where d (A, BC)represents distance of point A from side BC
View Solution
